运用发散型习题培养学生的发散思维

颜茂龙

【摘要】数学习题的教学对学生发散思维的培养有至关重要的作用,特别是发散型习题对学生发散思维的形成和发展有直接的推动作用,对学生的能力发展起着催化剂作用。在教学过程中,教师对习题的选择要有针对性,要切实有效地运用发散型习题培养学生发散思维。

【关键词】数学教学发散型习题发散思维

初中生的思维定势是一种普遍的心理现象。在学生的学习中,既有积极的作用,也有消极的作用。积极的作用表现在:学生按常规的思维模式去学习和发散思维能力的发展。初中数学这门学科对学生的发散思维要求比较高,培养学生的发散性思维是数学教师努力的方向。对学生加强思维发散型习题的解题指导和练习训练,是培养学生发散思维有效途径之一。下面我结合实例谈谈个人的做法与体会。

案例一:菱形有哪些性质?如何判断一个四边形是菱形?

菱形是一种特殊的平行四边形,除具有平行四边形所有的性质外,还具有以下性质三个性质:(1)四条边都相等;(2)对角线互相垂直;(3)没一条对角线平分一组对角。

判断一个四边形是菱形的方法:

(1)四条边都相等

(2)对角线互相垂直的平行四边形

(3)有一条对角线平分一个内角的平行四边形

发散型习题1:在四边形ABCD中,对角线AC、BD交于点O,从(1)AB=CD;(2)AB∥CD;(3)OA=OC;(4)OB=OD;(5)AC⊥BD;(6)AC平分∠BAD这六个条件中,选取三个推出四边形ABCD是菱形,如(1)(2)(5)推出四边形ABCD是菱形。再写出符合要求的两个:___________推出四边形ABCD是菱形;____________推出四边形ABCD是菱形;

分析首先依据题意画出图形如下,

再联想平行四边形及菱形的判定方法,

由“对角线互相垂直的平行四边形”是菱形可得(3)(4)(5);由“有一条对角线平分一个内角的平行四边形”是菱形可得(1)(2)(6)或(3)(4)(6)。

答案:(3)(4)(5)(1)(2(6)

变式演练1如图所示,菱形ABCD的周长为40cm,∠BAD=120°,对角线AC的长为()

A. 5cmB.5(根号下3)cmC.10cmD. 103cm

发散型习题2:已知□ABCD,试用两种方法将平行四边形ABCD分成面积相等的四个部分。

分析:平行四边形是中心对称图形,过对称中心的每一条直线可将平行四边形ABCD分成面积相等的两个部分。由于平行四边形对边平行,而两条平行的距离相等,可利用等底等高的三角形面积相等这一条件。

解方法一:连接AC、BD。如下图所示。

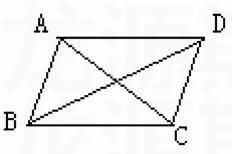
方法二:过对称中心分别作平行于AB、CD的平行线EF、MN即可。如下图所示。

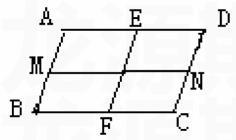
方法三:过AD、BC的中点作直线EF,连接BE、DF即可。如下图所示。

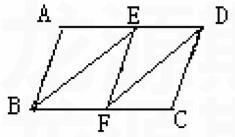
案例二:等腰梯形的性质和判定

等腰梯形的性质:等腰梯形同一底上的两角相等,对角线相等。

等腰梯形的判定方法:

发散型习题1如下图所示在等腰梯形ABCD中,AB∥CD,AB>CD,AD=BC,BD平分∠ABC,∠A=60°,梯形的周长为20cm,试求梯形的面积。

分析:由等腰梯形的性质,可知∠A=∠ABC=60°,由BD平分∠ABC,可得∠2=∠3=30°,则∠ADB=90°,因此有BC=DA=1/2AB,可求出上下底的长及梯形的高。

解在等腰梯形ABCD中,∠A=∠ABC=60°。

∵BD平分∠ABC,∴∠2=∠3=30°

∵∠ADB=180°—(∠A +∠3)=180°—(60°+30°)=90°,

∴AB=2AD。

∵AB∥CD,∴∠1=∠3,进而∠1=∠2。

∵CD=BC=AD。

∵AD+CD+BC+AB=20

∴CD=4,AB=8,AD=4。

作DE⊥AB,垂足为E,则∠ADE=30°

∵AE=1/2BD=2,

∴DE=

∵S_梯形ABCD=(CD + AB)•DE =

发散型习题2如下图,在梯形ABCD中,AD∥BC,∠B=∠C,点E是BC边的中点,求证:AE=DE。

分析要证AE=DE,可证△ABE≌△DCE,联想等腰梯形的判定定理和性质定理。

证明在在梯形ABCD中,

∵∠B=∠C,

∴梯形ABCD是等腰梯形。

∴AB=DC。

∵点E是BC边的中点,

∴BE=CE

∴△ABE≌△DCE,∴AE=DE。

发散型习题3(本题由学生自主完成,教师检查、点拨):在数学活动课上,要求同学们做下面的“循环分割”操作,然后再探索规律:如下图是一等腰梯形纸片,其腰长与上底长相等,且底角分别为60°和120°,按要求开始操作(每次分割,纸片不得有剩余)。

第1次分割,先将原等腰梯形纸片分割成3个全等的正三角形,然后将出的一个正三角形分割成3个全等的等腰梯形。

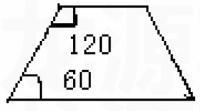
第2次分割,先将上次分割出的3个等腰梯形中的一个分割成3个全等的正三角形,然后将刚分割出的一个正三角形分割成3个全等的等腰梯形;以后按第二次分割的方法进行下去……

(1)请你在下图中画出第一次分割的方案图

(2)若原等腰梯形的面积为a,请你通过操作、观察将第2次、第3次分割后所得的最小的等腰梯形面积分别填入下表:

(3)请你猜想,分割所得的一个最小等腰梯形的面积S与分割次数n有何关系?(请直接用含a的式子表示,不需写推理过程)。

总之,数学习题的教学对学生发散思维的培养有至关重要的作用,特别是发散型习题对学生发散思维的形成和发展有直接的推动作用,对学生的能力发展起着催化剂作用。在教学过程中,教师对习题的选择要有针对性,要切实有效地运用发散型习题培养学生发散思维。