地区环境治理综合评价方法创新
刘文昌
中图分类号:F124.5 文献标识码:A
内容摘要:综合评价方法可以对多方案决策问题提供科学依据。目前,用于综合评价的各种方法存在固有局限,导致评估值的大小取决于权重系数的选择,造成系统的实际运行情况或被权重系数“增值”,或被权重系数“贬值”,形成系统的“变异”发展。本文介绍一种能在整体上“削弱”权重系数的作用,在局部中却能突出其作用的综合评价新模式,并通过在地区环境治理水平的综合评价实例中的应用加以阐释。
关键词:综合评价 权重系数 环境治理
综合评价概述
综合评价是指对被评价对象所进行的客观、公正、合理的全面评价。一般来说,被评价对象会有多个子系统。所谓的系统综合评价,就是指通过一定的数学模型将多个子系统的评价指标值“合成”为一个整体性的综合评价值。
目前,国内外文献中用于“合成”和综合评价的数学方法较多。常用的有线性加权综合法、非线性加权综合法、增益型线性加权综合法和理想点法等等。Carrizosa等对于权重因子给予了充分的阐述;而Cook等对分层评价进行了详细研究;对于多层决策的敏感性分析,Traintaphyllou等进行了深入探讨;我国学者郭亚军等则对最优决策的预测方法进行了研究。
本文为了克服上述方法的固有局限(评估值的大小取决于权重系数的选择,从而在已确定评价指标值的情况下,系统的实际运行情况或被权重系数“增值”,从而产生盲目乐观情绪;或被权重系数“贬值”,导致系统的“变异”发展,这几种情况显然都不利于系统的协调发展),给出一种能在整体上“削弱”权重系数的作用,在局部中却能突出其作用的综合评价新模式,并在地区环境治理的综合评价中进行了实际应用。
综合评价新模式基本思想
当极大型指标(指标取值越大越好)Xj(j=1,2,…,m)的取值(经过无量纲化处理,以下相同)都很接近于1时,那么系统的运行状况就可认为是整体协调的,因而它的整体效益高;当Xj(j=1,2,…,m)的取值都很接近于0时,系统的运行状况虽然也是相对整体协调的,但其整体效益偏低;当某个或某几个指标的取值都比较大(比如很接近于1),而其他指标的取值都比较小(如接近0)时,就认为这样的系统的运行状况是整体不协调的,因而其整体效益不高。基于此,本文给出如下基本思想:
首先定义D={x=(x1,x2,Λ,xm)T│Xk∈[0,1]}为系统的状态空间,x称为状态变量。
定义1:对取定的X*=(X1*,X2*,Λ,xm*)T∈D(Xj*>0),对任意的X=(X1,X2,Λ,xm)T∈D,若有不等式Xj≥Xj*(j=1,2,Λ,m)成立,则称x连同X*为D中的准有效点。其中X*是针对系统的设计(或期望)而预先设定的。D中所有的准有效点构成的集合称为D的准有效子集,并记为A。
定义2:对取定的X**=(X1**,X2**,Λ,xm**)T∈D(Xj**>0),对任意的X=(X1,X2,Λ,xm)T∈D,若至少对某一个k,有不等式Xk<Xk**成立,则称x连同X**为D中的非有效点。其中X**也是针对系统的设计(或期望)而预先设定的。D中所有的非有效点构成的集合,称为D的非有效子集,并记为C。
令集合B=D-A-C,则有D=AYBYC,但AI B=BI C=CI A=φ。由定义1及定义2知,落在子集A内的点(即系统),就是其协调发展、整体效益高的系统;落在子集C内的点,就是其协调发展的程度差、整体效益偏低的系统。
定义了状态空间D的准有效子集A及非有效子集C之后,作如下规定:落在子集A内的点,称其为第I类发展水平的;落在子集B内的点,称其为第II类发展水平的;落在子集C内的点,称其为第III类发展水平的。
进而,本着先注重系统的整体效益,其次注重局部效益的评价原则,先将落在D内的系统划分为三个类别;然后,为突出系统的局部效益,可针对每一类别内的系统,分别选择权重系数,对各个类别内的系统进行综合评价并排序。
假定有n个点(即系统)落在D内,且设A中有n1个点xi(1)(i=1,2,Λ,n1),B中有n2个点xj(2)(j=1,2,Λ,n2),C中有n3个点xk(3)(k=1,2,Λ,n3),n1+n2+n3=n。分别针对{xi(1)}、{xj(2)}、{xk(3)},确定出相应的权重系数{wj(k)}(j=1,2,Λ,m;k=1,2,3),即得相应的综合评价模型(i=1,2,Λ,nk;k=1,2,3)。按yi(k)的值由大到小分别排序,即达到对集合A、B、C内的系统的指标状况进行综合评价的目的。同时,根据对实际评价对象的要求,也可同时对单个集或两个集内的系统进行综合评价及排序。
综合评价新模式应用实例
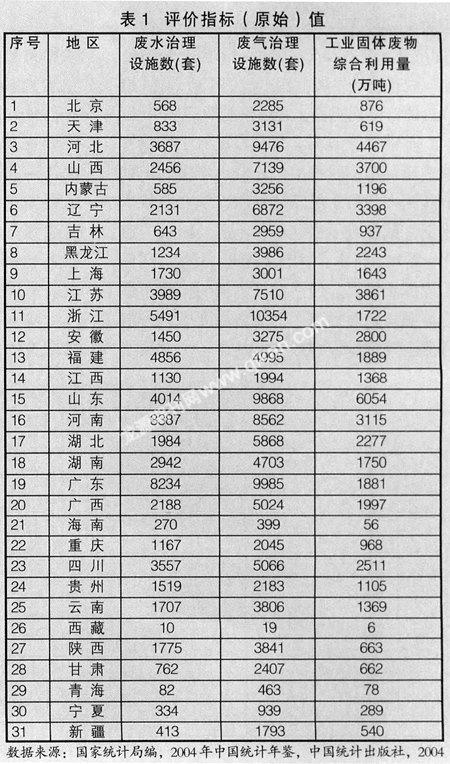
以综合评价我国31个省区在2003年的环境治理状况为例,取3项评价指标分别为:废水治理设施数(套)、废气治理设施数(套)、工业固定废物综合利用量(万吨),并依次记为x1,x2,x3,三项指标均为“极大型”指标,其原始数据,如表1所示。
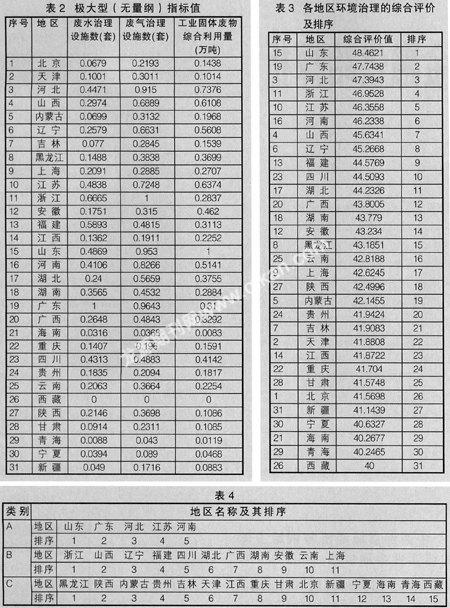
由于表1中三项指标的量纲不一致,故需对其进行无量纲化处理。利用模型(i=1,2,3) (其中为无量纲化后的指标值,mi为指标xi中的最小值)对三项指标进行无量纲化处理,如表2所示。
确定出权重系数W=(0.2598,0.4357,0.3044)T,计算系统的综合评价值yi(k),通过MATLAB程序拟合出各地区环境治理比较图,并按yi(k)的值由大到小进行排序,如表3所示。
根据无量纲的指标值,计算=
0.254241935,0.426403226,0.297912903)T,取x*=1.2=(0.305090323,0.511683871,0.357495484)T及x**=0.6=(0.152545161, 0.255841935,0.178747742)T,将31个省区分别划入集合A、B、C内,如表4所示。
由表4可知,山东、广东、河北、江苏、河南属于第I类环境治理水平;浙江、山西、辽宁等11个地区属于第II类环境治理水平;其余15个地区的环境治理水平属于第III类水平。浙江的环境治理水平,在B内排在第一位,而在D内排在第四位。事实上,浙江虽然在某些方面有很大的局部效益,但因其“工业固体废物综合利用量”指标x3取值偏小(x3=0.2837),而将其划分到第II类中是比较合乎实际的。
结论
本文所介绍的这种先分类后排序的综合评价模式尽管在计算上相对麻烦一些,但却有如下特点:在总体上削弱权重系数的作用,而在局部却突出权重系数的作用,从而避免了综合排序的“串套”现象,使综合评价及排序的结果更符合实际情况;避免了由于过分强调某个(或某些)指标权重系数的作用而导致系统“变异”发展的危险倾向;在客观上可起到促进系统协调发展的积极作用;指标评价最大限度地减少了主观色彩;既注重系统的整体效益,又突出系统局部效益。
参考文献:
1.郭亚军.综合评价理论与方法[M].科学出版社,2002
2.郭亚军.多属性综合评价[M].东北大学出版社,1996
3.国家统计局编.2004中国统计年鉴[M].中国统计出版社,2004

