设计“高价值”的习题

杨生斌　黄红成

习题是教材的重要组成部分，习题教学是课堂教学不可忽视的内容，是落实教学目标的重要环节。根据教学目标的不同，我们可以把习题分为两类：一类是以夯实基础、巩固新知为主要目标的习题，一类是以训练学生思维、提高学生解题能力为主要目标的习题。比较这两种类型的习题，笔者认为，后者具有更高的教学价值，应引起习题设计者的高度关注，成为我们的追求。但是，现实中的课堂，不少老师对此似乎有所忽视，不仅未能充分挖掘教材中习题的内涵和发挥它们的教学价值，而且对教材习题机械处理、浅显教学，习题的教学价值难以体现，使之沦为课堂教学的“软肋”。那么，怎样设计“高价值”的习题呢？如下是笔者的一点思考和做法，仅供

大家参考。

一、 高价值的习题应该具有思维含量

有些课，新知教学部分，教师教得到位，学生学得扎实，可到了练习环节，教师似乎出于夯实学生基础的目的，一味地按教材中习题的编排顺序亦步亦趋地教学，学生的基础虽然扎实了，但思维却没有得到最大的发展。能力也没有得到最大的提高。且不说“解决问题的策略”之类的内容，就以概念教学为例，在新知部分让学生掌握概念意义能够进行简单判断以后，还应设计一些需要学生综合所学知识、有一定思维含量的问题。例如，在教学“比的意义”的课尾，可以先让学生了解并理解“人的体重与血液之比大约为13∶1，身高与脚长之比大约为7∶1”中两个比的意义，然后出示：

一个小区发生了一起盗窃案，经过侦察，警方在案发现场收集到罪犯的脚印，长24厘米。并且抓获了三名嫌疑犯，三人都没有承认谁是罪犯。

嫌疑犯档案：

甲体重63千克，身高173厘米，自行车修理工。

乙体重56千克，身高168厘米，某厂临时工人。

丙体重60千克，身高165厘米，无正当职业。

让学生根据这些资料思考谁的嫌疑最大。在解决问题的过程，学生既要联系自己的生活经验结合三名嫌疑人工作情况进行判断，又要根据案发现场的脚印和嫌疑人脚长的比率进行判断，还要结合这些情况辨别判断的主要依据和排除次要的因素（即体重）。虽然头绪稍多，但是学生个个跃跃欲试、兴趣盎然，不仅发展了他们的思维能力，提高了解决实际问题的能力，而且感受到了数学知识的魅力。当然，有思维含量的习题并非难题、怪题。

二、 高价值的习题应该饱有数学趣味

心理学研究表明，教学进入巩固阶段后，学生容易产生疲劳感，如果此时不关注学生的学习状态，适时设计一些学生感兴趣的习题，激发他们持续探究的欲望，通常难以达到理想的练习效果，因此，我们可以从题型和内容两方面入手，设计一些新颖的或学生喜闻乐见的题目实施教学。就拿“倍数和因数”的复习教学来说，由于概念多、内容杂，而且容易混淆，所以很难让学生以一种积极的情感参与学习，为此，笔者借鉴学生比较熟悉的综艺节目形式，设计了这样一些问题：

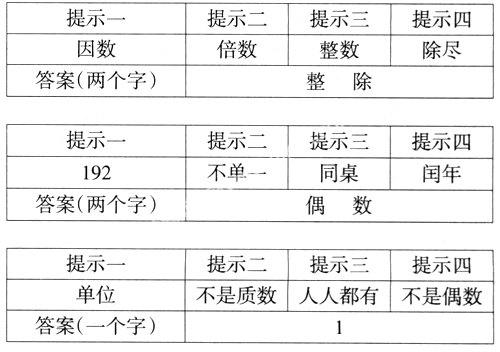
显然，将一些倍数和因数的相关概念整合起来，用“联想”的方式呈现在学生的面前，激起了学生学习兴趣的同时，也让学生认识到概念之间的联系。

三、 高价值的习题应该具有现实意义

数学源于生活，又回归于生活，与现实生活有着重要联系。提高学生解决实际问题的能力是数学教学的一个重要目标，设计具有现实意义的习题便是其有效途径之一。在教学中，一些老师虽然能有意识地设计一些具有生活味的习题，但总有“不到位”的感觉，习题的教学价值不高。例如教学“平行四边形的面积公式”时，他们往往让学生仅计算一些已知底和高或有多余条件的问题，这样教学，虽然学生对“如何计算平行四边形的面积”、“计算平行四边形的面积时需要知道哪些数据”等浅显问题有所了解，也初步掌握了计算平行四边形面积的方法，但是学生未曾接触“如何测量数据”、“如何选取、使用材料”等实际问题不能不说是个遗憾，因为这些问题通常是现实中首要和常见的问题，所以，仅此操作，学生解决实际问题的能力并不能真正得到最大限度的提高。为此，我们可以给每个学生准备一张相邻两条边分别是5厘米和4厘米的平行四边形，提问：（1）要求这个平行四边形的面积，你会怎么办？请你想办法算一算；（2）从这个平行四边形中能不能剪下一个长4厘米，宽3厘米的长方形，为什么？（图略）显然，设计这样具有现实意义的习题，给学生搭建解决实际问题的平台，既彰显

了习题的价值，又提高了教学的效益。

四、 高价值的习题应该具有教育功能

可以说，习题的教学价值不仅仅是为了巩固新知、形成一定的技能，还承载着让学生能够辨别是非和在品德方面得到教育和提高的目的。因此，在教学中，我们应该结合教学内容不失时机地落实这些教学目标，渗透品德等方面的教育或影响。例如在教学“统计表”时，不妨设计这样一道习题：下面是一张随机对80名大学生进行“未来最具发展潜质的人”的问卷调查表。

①把上面的统计表补充完整；②从表中的数据可以看出（）。

借助第②个问题，不但可以锻炼学生分析问题、解决问题的能力，而且在很有说服力的数据面前，不用说教，学生也能深刻认识到“未来最具发展潜质的人”的特点，潜移默化地受到人生观的教育。

五、 高价值的习题应该关注个体差异

学生是有差异的，数学教学应该关注每个个体的差异，让不同的学生的数学上都能得到发展。有价值的习题也应该关注学生的个体差异，让不同的学生都能得获得成功、得到发展，高价值的习题更需如此。然而在教学中，教师让学生练习的要求常常是统一的要求、统一的评价标准，学生的个体差异得不到重视。例如教学“除法的一些简便算法”时，从巩固直至下课，只见教师一组接一组地出示习题，能力强的学生还勉强能够应付，而能力弱的学生只有“疲于奔命”，忙得不可开交，至于对计算方法的思考更难以企及。为了切实关注学生个体计算能力的差异，提高习题练习的价值，课尾我们可以设计如下具有弹性的计算题组：

看看谁最棒（3分钟）：

计算一级能手: 180÷12÷5；210÷15÷2；280÷35； 4800÷32；

计算二级能手：计算一级能手中的习题； 540÷45÷2； 720÷5÷72；

计算一级高手：计算二级能手中的习题； 630÷18；720÷（8×6）；

计算二级高手：计算一级高手中的习题； 140÷35； 137×28－28×47；

这样的计算题组，一方面，学生为了争取较高级别的“美誉”，人人争先恐后，产生了不同的计算需求；另一方面，具有层次性的习题也吻合了不同层次学生的能力现状，给每个学生都提供了享受成功、品尝喜悦的机会，“关注个体差异”的教学理念得到了充分的体现。

习题教学是课堂教学的重要内容，也是落实教学目标的重要环节。教学中，我们应该高度重视习题教学环节，精心设计有利于较大限度发展学生思维、激发学生学习兴趣、提高学生解题能力和关注学生个体差异的高价值的习题，只有这样，才能彰显习题的教学价值，丰富教学的内涵，勃发教学的魅力，切实提高课堂教学的效益