遗传算法在物流配送路径优化问题中的应用

郭淑红　杨晓慧

[摘要]遗传算法是一种基于自然进化原理的全局搜索随机算法。遗传算法在物流管理的运输问题、布局问题、选址问题、配送问题、调度问题等方面应用非常广泛。首先建立物流配送路径优化问题数学模型，在此基础上构造求解物流配送路径优化问题的遗传算法。用此遗传算法进行物流配送路径优化，可以方便有效地求得问题的最优解或近似最优解。

[关键词]物流配送 遗传算法 优化

中图分类号：O29 文献标识码：A 文章编号：1671-7597（2009）0110046-01

一、引言

当前在解决物流配送车辆调度问题上有很多种算法，如神经元网络、蚁群算法（Ant Colony Optimization）等，但运用最多的是启发式算法，其中又有遗传算法、模拟退火算法、爬山算法、禁忌搜索算法等。

遗传算法（Genetic Algorithms，简称GA）是J.Holland于1975年受生物进化论的启发而提出的。遗传算法将问题的求解表示成“染色体”的适者生存过程，通过“染色体”群的一代代不断进化，包括复制、交叉和变异等操作，最终收敛到“最适应环境”的个体，从而求得问题的最优解或满意解。

该算法包括以下6个基本要素：(1)编码；(2)生成初始种群；(3)评估适应度；(4)选择：根据“适者生存”的选择原理；(5)交叉；(6)变异。

二、问题的提出

假定一配送中心，向n个顾客运送货物，每个顾客对货物有一定的需求量，货运车在配送中心配装发车后，把货物送到各顾客处，如何确定费用最小的车辆行驶路线?问题的关键是如何合理安排车辆数目和车辆路线，使得总的旅行路程最短。

三、问题的分析

为便于讨论，对问题做几点假设：

1．被配送的是已知的同一种物资；

2．各用户的所在地已知；

3．各用户的需求量已知；

4．从配送网点到各用户之间的运输距离已知；

5．配送网点有足够的资源可以供应配送，并且拥有足够的配送能力。

另外，配送计划中的最优发车路线，必须符合下列约束条件：

1．配送必须满足所有用户的需求；

2．对每一辆发送车的装载量有一定的限制，不允许超载运行；

3．对发送车每天的总运行时间（或总运行距离）有预定的上限；

4．必须满足用户提出的到货时间要求。

对一个具体的问题，上述约束条件可能全部存在，也可能只存在一部分。解决配送问题就是在以上约束条件下应如何派送车辆，给出车辆数、型号和各车辆的具体行车路线。订单上的货物全部送到即可完成当日的运输任务，又可以使总运输公里数最小。

物流配送路径的优化可以描述为：从配送中心用多辆汽车向多个客户送货，每个客户的位置和需求量一定，每辆汽车的载量一定，要求合理安排汽车路线，使总运距离最短，并满足以下条件：

1．每条配送路径上各个客户的需求量之和不超过汽车载量；

2．每条配送路径的长度不超过汽车一次配送的最大行驶距离；

3．每个客户的需求必须满足，且只能由一辆汽车送货。充分考虑上述问题的约束条件和优化目标。

四、优化算法优化物流配送路径遗传算法的构造

针对优化物流配送路径的特点，本文构造了求解该问题的遗传算法。

（一）编码方法的选定。采用二进制编码，用0表示配送中心，用1表示某个客户（L个1表示有L个不同的客户）。由于配送中心有K辆汽车，则最多存在K条配送路径，每条配送路径都始于配送中心，也终于配送中心。这样，L个1或K-1个0随机排列成一条染色体（N+K-1位），对应于一种配送路径方案。

（二）初始种群的生成。随机产生一个L个1和K-1个0的序列，形成一条染色体（个体位串），M条不同的染色体构成初始种群（设种群大小为M）。

（三）适应度评估。要评判某条染色体所对应的配送路径方案，既要看其能否满足配送的约束条件，又要计算其目标函数值，本文使用的编码方法，能够保证每个客户都得到配送服务，及每个客户仅由一辆汽车配送的约束条件，但不能满足每条路径上各客户需求量之和不超过汽车载量及每条配送路线的长度不超过汽车一次配送的最大行驶距离的约束条件。所以，对于每条染色体所对应的配送路径方案，要对各条路径逐一进行判断，看其能否满足约束条件：如果不满足，则该条路径为不可行路径，并计算其目标函数值。

（四）选择操作、结合使用最优个体保留策略和轮盘赌法，将每代种群中的N条染色体按适应度从大到小排列。适应度最高的染色体，复制直接进入下一代。然后，根据种群的N条染色体的适应度。采用轮盘赌法产生下一代种群的另N-1条染色体。方法为计算出种群中所有染色体适应度的总和（∑Fi）；再计算每条染色体的适应度所占的比例（Fi/∑Fi），作为其被选中的概率Psi。

（五）交叉操作。选择操作产生的新种群，除第一条染色体外，另N-1条染色体要根据交叉概率Pc进行交叉配对，可以采用一种改进的两点交叉法。

（六）变异操作。适度的变异，既能保持种群内个体的多样化，又能提高遗传算法的效率。根据变异概率Pmi一旦染色体的某基因片段需要发生变异，则染色体上的另一片段也要同时发生变异。

五、实例

某配送中心用2辆汽车对8个客户配送货物。设汽车的载量为8×103kg。每次配送的最大行驶距离为40km，配送中心与客户、客户与客户之间的距离及各客户的需求量见下表。在实验中采用了以下参数值：种群大小M取50，交叉概率Pc取0.65，变异概率取0.005，终止代数T取100。权重因子取100km。

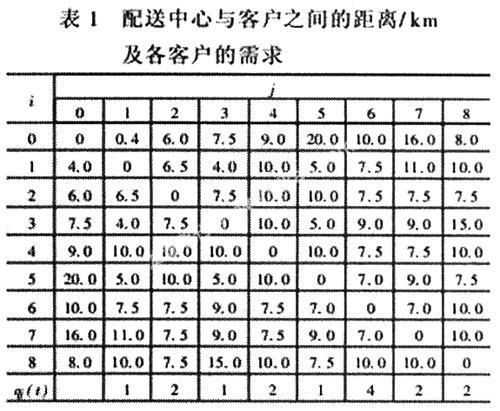
一共求解10次得出的结果都优于节约法所求得的结果（79.5km）。且第5次还得到了最优解67.5km，其对应的配送路径方案为：1-1-1-0-1-1-1-1-1-0（具体配送路径为4-7-6-0-2-8-5-3-1）。

参考文献：

[1]陈国良、王煦法、庄镇泉等，遗传算法及其应用[M].北京：人民邮电出版社，1996.

[2]李军、郭耀煌，物流配送车辆优化调度理论与方法[M].北京：中国物资出版社，2001.

[3]赵刚，物流运筹[M].成都：四川人民出版社，2002.