堰塞坝渗透稳定性评估

严祖文，魏迎奇，蔡 红

堰塞湖是一种常见的现象，它主要是由降雨、地震、火山及冰川引起的，多发生在高山峡谷区。这些地区构造活动强烈，地震、火山活动频繁，岩层节理、裂隙发育，易发生滑坡。“5．12”汶川特大地震中诱发了34处规模较大的堰塞湖，影响巨大，特别是唐家山堰塞湖，其坝体高度、体积，蓄水量、影响范围等在已知的堰塞湖史上均属前列，引起了全国广泛关注和重视。堰塞湖的存在对上下游区域造成严重的影响，对上游的危险主要是湖水淹没库区，而对下游的危险主要是堰塞坝突然溃坝，堰塞湖中的大量蓄水快速下泄，巨大的洪水将淹没下游，引起洪灾。因此，考虑堰塞坝自身的工程地质问题，确定性评估应包括渗透稳定性、抗滑稳定性和抗冲刷稳定性3个方面。通过分析，以明确堰塞坝坝体可能的破坏成因，并采用相应的工程处置措施。本文将主要讨论堰塞坝渗透稳定性评估。

1 堰塞坝渗透稳定性评估

1．1 渗流计算方法

1．1．1 非稳定渗流计算分析方法

非稳定渗流场指其基本表征量随时间而变化的渗流情况，即

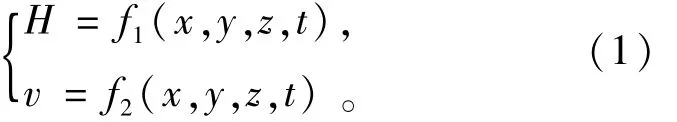
考虑压缩性的非均质各向异性，非稳定渗流微分方程式

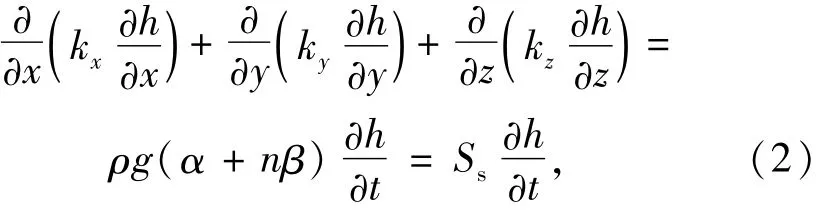
式中：h＝h（x，y，z，t）为待求水头函数；kx，ky，kz为以x，y，z轴为主方向的渗透系数；Ss为单位贮水量或贮存率其中Ec为弹性模量。

对均质各向同性材料，式（2）变为

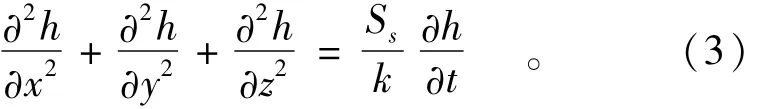
非稳定渗流有限元计算公式为

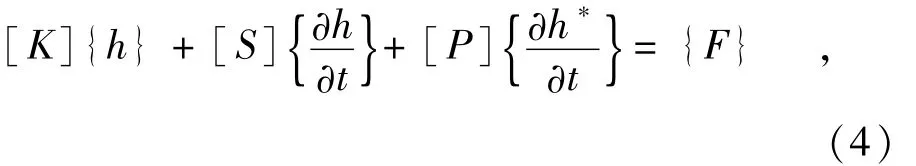
式中：［K］为总体渗透系数矩阵；｛h｝为各结点水头向量；［S］为压缩土体内部单元贮水系数矩阵；h 为自由面上的结点水头为流量补给和自由面单元的流量变化项；｛F｝为已知常数项，由已知结点水头确定。

1．1．2 稳定渗流计算分析方法

根据达西渗透定律，x，y，z方向的渗透流速可分别表示为

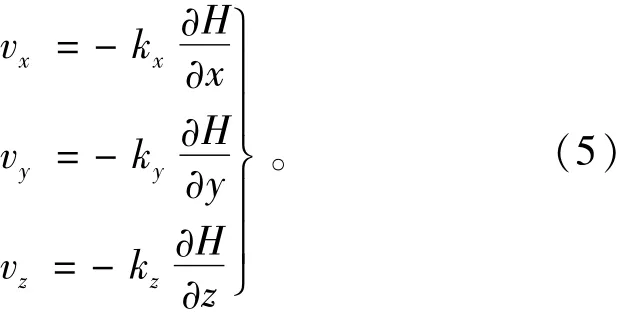
式中H为总水头。

将式（5）代入下式

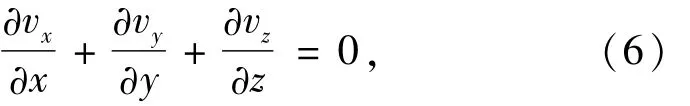
得到

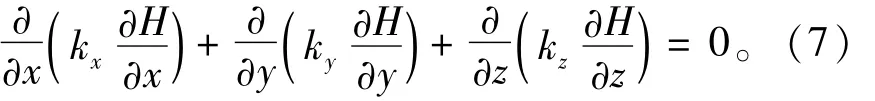
式（7）即为描述无源汇和各向异性稳定渗流场的基本微分方程。

对于各向同性渗流场，即当kx＝ky＝kz＝k时，式（7）变为

式（8）即为著名的拉普拉斯（Laplace）方程。

对于具有恒定降雨入渗或蒸发量ω的水平面稳定渗流场，其基本微分方程可写作

式中：Kx，Ky分别为x，y方向的导水系数，它等于相应渗透系数（k）与无压渗透深度（h）或有压含水层厚度（T）的乘积。

对于各向同性渗流场，即当Kx＝Ky＝K时，式（9）变为

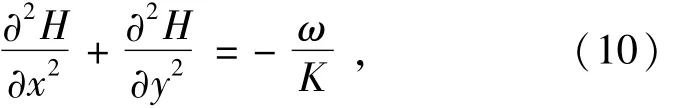
式（10）即为著名的波松（Poisson）方程。

稳定渗流有限元计算公式为

1．2 渗流计算内容

1．2．1 非稳定渗流计算

非稳定渗流计算的目的主要是了解堰塞坝形成后，堰塞湖水位上升或下降过程中坝体内的渗流场发展变化的规律、堰塞坝遭遇长期降雨时的渗流场发展变化特征以及判别非稳定渗流期坝体的渗透变形或破坏的可能性。

1．2．2 稳定渗流计算

堰塞坝形成之初，如果上游来水量较小且坝体的渗透性较低，则在短期内难以在坝体内形成稳定的渗流场；反之如果上游来水量较大，坝体渗透性较强，则在坝体内就会很快形成稳定渗流场。因此对于堰塞坝而言，应将不同上游水位条件下的稳定渗流作为控制工况来考虑。

1．3 渗流计算工况和渗透系数的确定

1．3．1 计算工况

非稳定渗流：①上游水位自堰塞坝形成初水位蓄至可能最高水位，如果最高水位超过堰塞坝坝顶，则最高水位按坝顶高程控制，下游水位按实际水位控制；②长期降雨入渗工况。

稳定渗流：①上游最高水位与下游实际水位组合；②上游不同高程水位对下游实际水位。

1．3．2 渗透系数的确定

一般在确定坝体材料的渗透系数时应考虑材料的颗粒组成、岩性特征、工程形成条件等因素，但在堰塞湖形成之初，由于信息缺乏，此时确定渗透系数，应尽可能根据现场表观地质概况，选取相近工程的类似地质条件类比确定。

1．4 渗流稳定性评价

1．4．1 允许比降的确定方法

对于流土型无黏性土可用下式计算允许比降，

对于管涌型的无黏性土可用下式计算允许比降，

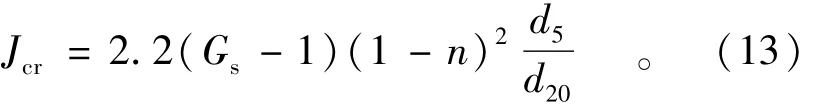
式中：Gs为土粒比重；d5为土粒粒径，小于该粒径的土质量占总土质量的5%；d20为等效粒径（mm），小于该粒径的土质量占总土质量的20%。

此外，如果条件允许，可能通过渗透试验来确定土的允许比降。

1．4．2 渗流破坏形式的判别

均匀无黏性土的渗透破坏形式只有流土一种形式，不均匀土的渗透破坏形式有管涌和流土2种形式，这主要取决于细料填充粗料孔隙的程度。细料填满粗料孔隙的土，渗透破坏形式为流土，否则为管涌型。无黏性土的渗透破坏形式的判别方法及判别标准如表1。

表1 无黏性土渗透破坏形式经验判别Table 1 Empirical discrimination of seepage failure form of cohesionless soil

表中D0按下式确定

式中：D0为土的孔隙平均直径（mm）；n为土的孔隙率（以小数计）。

1．4．3 渗透稳定性判别

根据确定的允许比降和计算得到的出逸比降，即可对坝体的渗透稳定进行评估。

当i＜i允许时，则土处于稳定状态。

当i＝i允许时，则土处于临界状态。

当i＞i允许时，则土处于破坏状态。

对于无试验资料的无黏性土，可以根据表2进行初判，表中的土类可根据表1进行判别。

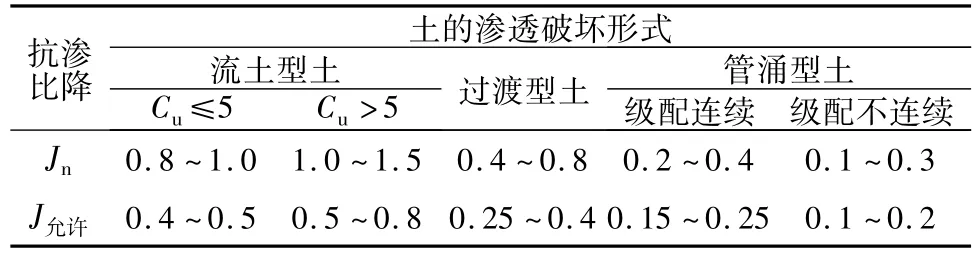
表2 各类土抗渗比降变化范围及允许值Table 2 Range and allowable value of anti－infiltration slope

2 唐家山堰塞坝渗流计算

2．1 渗透系数确定

以唐家山堰塞坝为例，坝体和坝基共分为黄色碎石土区、强风化碎裂岩区、弱风化碎裂岩区、灰黑色含泥粉细砂和基岩5个区。在考虑材料分区不失真的情况下，对坝体和坝基材料进行概化如图1。

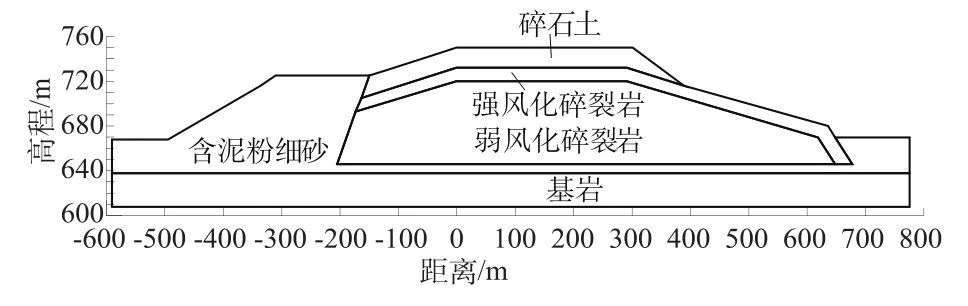
图1 渗流有限元计算概化模型Fig．1 Model of seepage finite element

在确定唐家山堰塞坝渗透系数时，根据工程地质资料，参考的相近工程包括由基岩塌滑形成的大海子坝［1］、武都县白龙江中游滑坡堵江工程［2］，以及通口电站大坝灌浆施工监理的实践［3］、岷江上游崩塌堵江次生灾害及环境效应研究［4］等相关研究成果，各区渗透系数取值见表3。

表3 材料渗透系数Table 3 Permeability coefficients of materials

2．2 渗流计算成果

非稳定渗流计算成果表明，至2008年5月31日堰塞湖蓄水位达到742．2 m高程并保持不变的条件下，在坝体内形成稳定渗流状态需要1．81年，下游坝坡出现水流逸出发生在259 d后，并逐步向上发展，最后在698．5 m高程停止（图2），下游坝坡最大出逸比降为0．11。

图2 非稳定渗流有限元计算结果Fig．2 Results of unsteady seepage finite element

稳定渗流计算结果表明，各种计算工况下下游坝坡的出逸比降均较小，对比材料岩性和颗粒造成特征，坝体基本不会产生渗透破坏（表4）。但由于材料的不均匀性，局部区域出现渗透破坏也属正常，建议加强下游渗漏的观测，特别是出逸处是否夹带颗粒，以避免渗透破坏造成严重的后果。

表4 渗流计算成果Table 4 Calculated results of seepage

3 结 语

（1）本文借助唐家山堰塞坝的渗透稳定性评估过程，考虑堰塞坝自身的工程地质问题，阐述了堰塞坝坝体渗流稳定性评价的基本方法和内容，确定了渗透破坏的形式和程度。

（2）通过对唐家山堰塞坝的渗透安全评估，各种计算工况下下游坝坡的出逸比降均较小，对比材料岩性和颗粒造成特征，其坝体的渗透稳定性能够满足安全要求。

［1］ 中国水利水电科学研究院抗震防护研究所．关于岷江上游叠溪大、小海子地震坝抗震稳定性的讨论［R］．北京：中国水利水电科学研究院，1993．

［2］ 原俊红．白龙江中游滑坡堵江问题研究［D］．兰州：兰州大学，2007．

［3］ 姚世军．通口电站大坝灌浆施工监理的实践［J］．四川建筑，2005，25（9）：187－189．

［4］ 严 容．岷江上游崩塌堵江次生灾害及环境效应研究［D］．成都：四川大学，2006．