日冕水电站心墙堆石坝坝体渗流场初步分析

朱国胜，张家发，王金龙

金沙江日冕水电站是金沙江上游河段9个梯级开发规划方案中的第8级。预可行性研究阶段，枢纽正常蓄水位2 380 m，相应库容62亿m3，装机容量3 200 MW，下坝址——斯木达（登木通）坝址适合修建心墙堆石坝，坝高达346 m。坝体渗流状态将直接关系到大坝的渗流安全，尤其是高水头和高应力条件下的坝体渗透稳定性更是需要重点研究的关键课题。为此，需要了解坝体的渗流分布规律，评价大坝渗透稳定性，为大坝分区设计及填料渗透性要求的确定提供依据。根据预可研阶段深度的需要，参照规范、已有工程资料及本工程的初步研究成果，初步确定了大坝各分区的渗透系数变化范围；并针对渗透系数组合、水位条件和心墙坡比拟定方案，开展了稳定渗流场计算；结合经验公式拟定给水度，开展了库水位骤降时上游坝壳料的渗流场计算与分析。

1 工程概况和地质条件

金沙江在斯木达坝址附近弯曲延伸，呈“S”型展布。坝址区基岩在风化轻微、岩体完整的状态下均属微－极微透水岩体，微新岩体基本上为相对隔水层，金沙江为地下水的最低排泄基准面。

枢纽布置由心墙堆石坝＋左岸溢洪道＋左岸泄洪洞＋右岸地下厂房组成；拦河大坝采用心墙堆石坝，坝顶高程2 386．0 m，坝顶长810．5 m，坝顶宽18 m；河床底高程2 065 m；心墙范围清除覆盖层，建基面高程最低2 040 m，最大坝高346 m。大坝上游坝坡为1∶2．25，坝体断面最大底宽约 1 700 m（沿河道）。

大坝坝体主要由防渗心墙、反滤料、过渡料和堆石体组成。心墙顶高程2 384．0 m，顶宽6 m，上、下游坡为1∶0．25，心墙底高程 2 042 m，最大底宽 177 m；心墙上、下游各设两道反滤层和一道过渡层，反滤层每层宽度4．5 m，过渡层顶部宽度10 m。心墙坝基础设置帷幕灌浆廊道，心墙范围设置混凝土垫层和固结灌浆。大坝典型横剖面图见图1。

2 计算模型、方案和参数

2．1 计算模型

基岩为微透水或不透水岩层，心墙直接建于不透水基岩上，选取坝体最大断面作为计算断面，进行二维渗流分析。概化断面见图2，图中各渗透分区分别概化为：防渗心墙（K1）；反滤层Ⅰ（K2）；反滤层Ⅱ（K3）；坝壳堆石区（K4）。

三维饱和非稳定渗流控制方程为

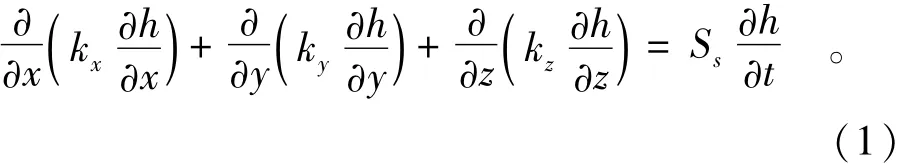
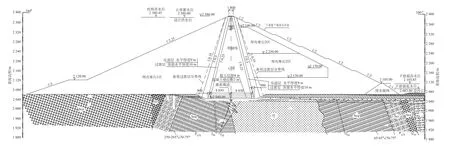
图1 大坝典型横剖面图Fig．1 Typical cross section of Rimian Rock Fill Dam

图2 坝体二维渗流计算概化模型图Fig．2 Cross section of FEM conceptual model

研究的渗流场为二维稳定渗流，对于均质各向同性介质，其基本方程为

边界条件为 水头边界：h｜Γ1＝f1（x，z），

稳定渗流上游水位边界、下游水位边界为给定水头边界（第一类边界）；稳定渗流中的自由面及不透水层面则属定流量边界（第二类边界），其法向流量为0。本文采用长江科学院渗流计算软件S3D和S2D分别开展稳定渗流场和非稳定渗流场计算。石坝设计规范》［1］要求心墙的渗透系数不大于1×10－5cm／s。在满足规范的前提下，以心墙的渗透系数1×10－5cm／s作为基本方案进行计算是合适的。

反滤料渗透系数的取值类比瀑布沟心墙坝和塔城心墙坝的反滤料试验结果。瀑布沟反滤料渗透系数在10－3cm／s量级。塔城反滤料I的渗透系数为10－5～10－4cm／s量级，反滤料II平均级配渗透系数为10－1～100cm／s量级。本工程采用的反滤料是一种人工加工的材料，参考同类工程、经验和设计要求，反滤料I渗透系数取1×10－3cm／s作为基本方案，反滤料Ⅱ取2×10－1cm／s作为基本方案。

参考塔城坝壳料渗透系数试验结果10－2～100cm／s，日冕坝壳料渗透系数取1×100cm／s作为基本方案。

综上所述，基本方案计算参数取值见表1。

2．2 稳定渗流计算的参数和方案

表1 大坝分区渗透系数取值范围及基本方案取值Table 1 Permeability coefficient range of dam zones and corresponding cofficient value for the basic case simulated

在土质心墙堆石坝的设计中，防渗土料的选择和设计至关重要。砾石土由于粒径尺寸分布较宽，颗粒组成具有一定的不均匀性，渗透性也有很大差异，因此砾石土心墙料的渗透性能直接影响到大坝的防渗效果，并成为决定高土石坝安全性的关键而敏感的指标之一。对于坝体填料的渗透性，要充分考虑可能的变化范围，为此，以日冕大坝填料试验成果为基础，参考国内其他心墙堆石坝的试验成果和工程碾压试验、施工检测资料，确定大坝分区渗透系数的敏感性分析范围和具体方案。

2．2．1 基本方案参数取值

对比同类工程，防渗心墙的渗透系数量级为10－7～10－4cm／s。本工程已经取得的渗透系数试验值多数处于10－6～10－5cm／s量级。《碾压式土

2．2．2 心墙的渗透系数敏感性分析

由于心墙填方量大，土料不十分均一，填筑密度一定差异，其渗透系数会在一定范围内变化，因此，充分考虑其变化范围，分析其对渗流场的影响是必要的。参照同类工程的资料［2－11］，防渗心墙渗透系数敏感性分析取值范围考虑为1．0×10－6～1．0×10－4cm／s，根据计算结果对比分析心墙的渗透性对坝体渗流场的影响。日冕心墙坝已取得的试验成果表明，心墙砾石土的渗透系数有一部分处于5×10－5～1×10－5cm／s之间。为偏于安全考虑，在进行坝体其他区渗透性及心墙设计尺寸比较计算时，心墙料均取为5．0×10－5cm／s。

2．2．3 反滤层Ⅰ的渗透系数敏感性分析

反滤层Ⅰ是一种人工加工材料，其渗透系数一般可以通过调整级配而得到控制，在对心墙料起到保护作用的同时，为了保证反滤层的排水效果，其渗透系数相对于心墙料来说应该足够大。结合其他工程经验，以1×10－3cm／s为基本方案取值；同时对反滤层Ⅰ渗透系数分别取 2×10－1cm／s、1×10－2cm／s和1×10－4cm／s开展渗流场计算，根据计算结果对比分析反滤层Ⅰ的渗透性对坝体渗流场的影响。

2．2．4 反滤层Ⅱ的渗透系数敏感性分析

反滤层Ⅱ也是一种人工加工材料，为满足反滤要求，其渗透系数应至少大于反滤层Ⅰ，但不应大于坝壳料渗透系数。结合其他工程经验，以2×10－1cm／s为基本方案取值，同时对反滤层Ⅱ渗透系数分别取6×10－1cm／s、1×10－2cm／s和 1×10－3cm／s开展渗流场计算，根据计算结果对比分析反滤层Ⅱ的渗透性对坝体渗流场的影响。当反滤层Ⅱ与反滤层Ⅰ渗透系数相同时，相当于只有一层反滤。2．2．5 坝壳堆石区的渗透系数敏感性分析

结合其他工程的经验，以1 cm／s为基本方案取值，同时对坝壳堆石区渗透系数分别取5 cm／s和2×10－1cm／s开展渗流场计算，根据计算结果对比分析坝壳堆石区的渗透性对坝体渗流场的影响。

2．2．6 不同水位组合条件下的渗流场对比分析

基本方案中水位条件：上游为设计水位2 380 m，下游为最低水位2 083 m，上下游水头差297 m。对比方案的水位条件：上游取校核洪水位2 380．45 m，下游水位对应取为最高水位2 103．85 m，上下游水头差276．6 m。通过特征水位组合条件下的渗流场计算，分析不同水位条件下的坝体渗流场分布。

2．2．7 不同心墙坡比的渗流场对比分析

心墙顶宽取6．0 m，在基本方案中心墙坡比为0．25，对比方案中心墙坡比分别为0．20，0．15。根据计算成果，对比分析不同心墙坡比对坝体渗流场分布的影响。

根据水位、渗透系数组合及心墙坡比等条件拟定15个计算方案，见表2。

2．3 非稳定渗流计算参数

由于水电站、大坝运行和检修的特殊需要，可能会出现快速降低库水位的工况。此时如果坝体内的孔隙水压力不能很快消散，出现坝体浸润线高于上游库水位的现象，可能对上游坝坡的稳定造成不利影响，严重的甚至导致上游坝坡失稳。根据本工程的运行特点，上游库水位可能在5 d内从2 380 m降至2 340 m，降速达8 m／d，因此有必要研究库水位下降过程中各时段的坝体浸润线位置。

表2 计算方案表Table 2 Cases to be simulated

坝体浸润线下降的速度，一般决定于库水位的下降速度v、坝体的渗透系数k以及土体的给水度μ等因素。有关规范推荐了判别方法：当k／（μv）＜0．1时，坝体内渗流自由面在库水位降落后仍保持有总水头的90%左右，可认为坝体浸润线基本保持原有位置不变；而当k／μv＞60时，坝体内自由面保持有总水头的10%以下，基本上与库水位同步下降，一般不需进行非稳定渗流计算，可以采用库水位降落后稳定渗流场的自由面计算分析坝体抗滑稳定性；当0．1＜k／μv＜60时，浸润线的下降介于上述两种情况之间，需要进行非稳定渗流计算分析，以确定浸润线的实际位置，作为抗滑稳定计算的渗流条件。

根据国内外砂砾石土和黏性土的试验资料，在没有试验资料时，给水度的取值可以参照经验公式，其中有毛昶熙（1981年）经验公式：

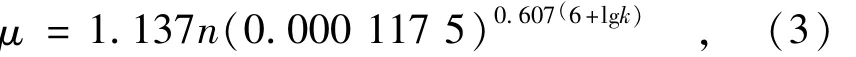
式中：n为孔隙率；k为渗透系数，cm／s。

别申斯基（1960年）经验公式：

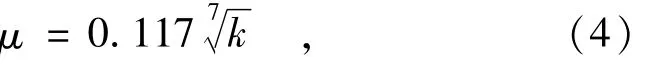
式中 k为渗透系数（m／d）。别申斯基公式一般只适用于粗颗粒土，不适用于颗粒小于细砂的土质。

本工程库水位下降过程中自由面变化范围内的土体有心墙料、反滤层（I，II）及坝壳料，心墙料渗透系数远比坝壳料小，而且其给水度很低，k／μv亦很低，对心墙而言，可以认为库水位是骤降，即浸润线在心墙内的降落属于缓降，在研究边坡稳定时，从安全的角度出发，可以采用水位降落前的浸润线进行分析。为简化考虑，在库水位降落期间只计算上游坝壳及反滤料部分的渗流场。然而按式（3）和式（4）计算的坝壳料的给水度及 k／（μv）判断，8 m／d的库水位下降对于坝壳料而言属于缓降，从工程安全的角度出发，进一步扩大考虑坝壳料渗透性的变化范围，取渗透系数为0．1 cm／s，拟定非稳定渗流计算方案，各参数的取值见表3。

表3 非稳定渗流计算参数取值Table 3 Parameters under calculation cases of unsteady seepage field

3 渗流计算及分析

3．1 稳定流计算成果分析

各方案的计算成果见表4，表中心墙、下游反滤层及下游堆石区承担的比降是评价坝体安全性的重要指标，心墙下游边自由面高程反映了心墙的防渗能力。图3为方案1的渗流场等势线分布图。

3．1．1 防渗心墙渗透系数对渗流场的影响

方案2，1，3和4的结果对比说明，心墙的渗透系数从1．0×10－6cm／s增大到1．0×10－4cm／s时，渗流场水头分布变化不大，心墙承担绝大部分水头，心墙承担的最大水平比降从2．56略降至2．45，心墙后自由面高程从2 372．3 m下降至2 371．57 m，反滤层Ⅰ最大水平比降从0．01增大至0．37。方案4中心墙的渗透系数为1．0×10－4cm／s时，反滤层Ⅰ的渗透系数为1．0×10－3cm／s，两者的渗透系数仅相差10倍，心墙仍承担97%以上的水头损失，尽管心墙的比降变化得不多，但使得反滤层Ⅰ的最大水平比降增大至0．37，这对于反滤层Ⅰ的渗透稳定是不利的，也对反滤层Ⅱ的反滤保护提出更高的要求。

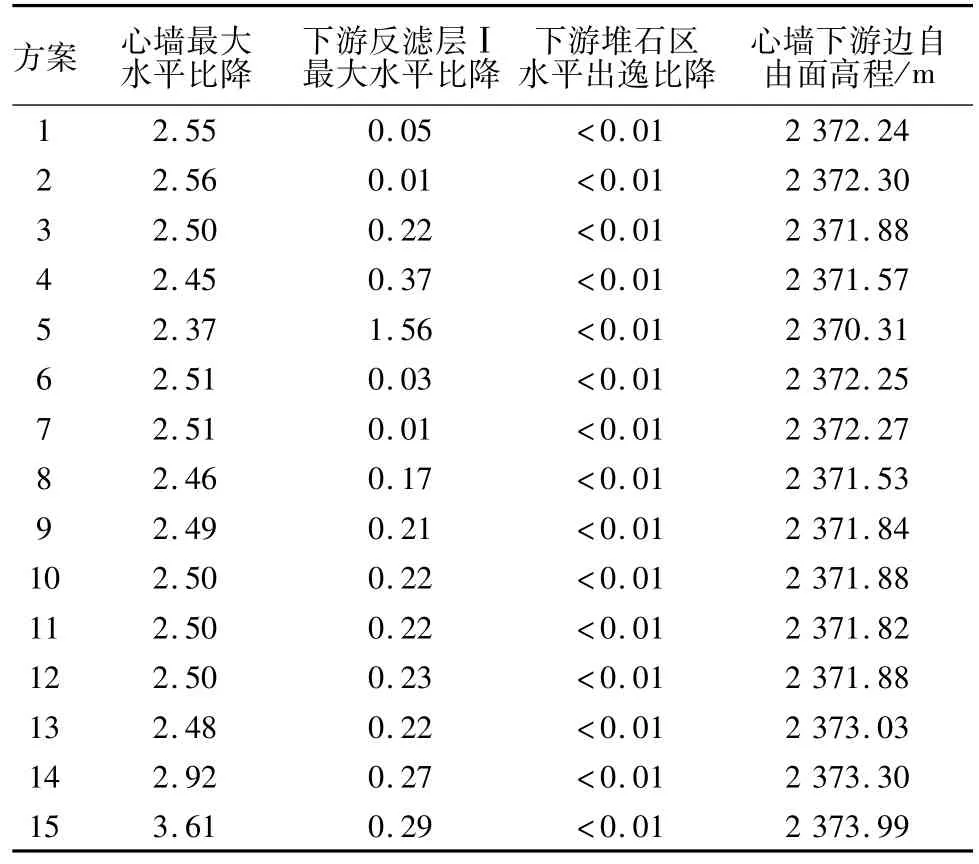
表4 稳定渗流场计算成果表Table 4 Simulated results of steady seepage field

图3 方案1渗流场等势线分布图Fig．3 Eequipotential lines of seepage field at case 1

从表4可以看出，心墙坡比为1∶2．5时，各方案中心墙承担的最大比降为2．37～2．56。已有的试验资料表明，日冕新村心墙料料场Ⅱ临界比降为5．49～11．08，允许比降为2．75～5．54（安全系数为2．0），心墙承担的最大比降小于其允许比降，具有一定的安全裕度，如果考虑反滤料的保护作用，心墙料的抗渗比降还可大大提高。根据同类工程资料［12－16］，心墙承担最大比降计算值为：瀑布沟2．10，水布垭心墙坝方案2．95～3．11，张峰水库大坝4．6～5．7，丹江口左联土石坝3．57～4．08。与这些工程相比，日冕大坝心墙料承担的比降处于中等。

3．1．2 反滤层Ⅰ渗透系数对渗流场的影响

方案5，3，6和7的计算结果对比说明，当心墙的渗透系数为5．0×10－5cm／s，反滤层Ⅰ的渗透系数为1．0×10－3～2．0×10－1cm／s时，心墙均承担绝大部分水头，4个方案之间心墙承担的比降差别极小，为2．50～2．51，反滤层Ⅰ的自由面高程为2 084．81至2 083．0 m，反滤层Ⅰ的最大水平比降为0．22～0．01。

方案5中，反滤层Ⅰ渗透系数为1．0×10－4cm／s（比心墙渗透系数仅大2倍）时，反滤层Ⅰ区上游侧自由面高程为2 359．7 m，下游侧自由面高程为2 083．0 m，这种情况类似于反滤层Ⅱ单层反滤，而反滤层Ⅰ承担的水平比降将达1．56，其安全性将严重依靠反滤层Ⅱ的反滤保护。

因此，为避免反滤层Ⅰ出现较大渗透比降，宜使反滤层Ⅰ的渗透系数至少比防渗心墙的渗透系数大1个数量级。

3．1．3 反滤区Ⅱ渗透系数对渗流场的影响

方案8，9，3和10的计算结果对比说明，当心墙和反滤区Ⅰ的渗透系数分别为5．0×10－5cm／s、1．0×10－3cm／s，反滤区Ⅱ的渗透系数从1．0×10－3cm／s增大到6．0×10－1cm／s时，心墙承担的比降从2．46略增大至2．50，反滤层Ⅰ的最大水平比降从0．17增大到0．22，反滤层Ⅰ上游侧的自由面高程从2 085．62 m降低至2 084．81 m。由于心墙承担绝大部分水头损失，而反滤区Ⅰ，Ⅱ的宽仅为4．5 m宽，因此当反滤层渗透性发生改变时对整体渗流场分布的影响并不明显，只是对与心墙下游边接触的局部略有影响。

3．1．4 坝壳堆石区渗透系数对渗流场的影响

方案11，3和12的计算结果对比说明，当心墙、反滤区Ⅰ、反滤区Ⅱ的渗透系数分别为5．0×10－5cm／s、1．0×10－3cm／s、2．0×10－1cm／s，坝壳堆石区的渗透系数从2．0×10－1cm／s增大到5 cm／s时，坝壳堆石区的渗透性对渗流场的影响很小，心墙和反滤料区承担的比降均无明显改变。这是因为心墙渗透性远小于坝壳堆石区，心墙承担了绝大部分水头损失。

3．1．5 不同水位条件对渗流场的影响

方案3和13的上下游水头差分别为297 m、276．6 m，分别对应于设计水位条件和校核洪水位条件，各分区的渗透性相同。计算结果表明，由于校核水位条件下尾水水位抬升近20 m，心墙后反滤层、坝壳堆石区内自由面随下游水位升高约20 m；但由于心墙承担绝大部分水头损失，坝体其他分区的比降变化很小。

3．1．6 心墙坡比对渗流场的影响

方案3，14和15的计算结果对比说明，当心墙、反滤层Ⅰ、反滤层Ⅱ、坝壳堆石区的渗透系数分别为5．0×10－5cm／s、1．0×10－3cm／s、2．0×10－1cm／s、1 cm／s，保持心墙顶宽6 m不变，坡比从0．25减小到0．15时，心墙底部宽度从178 m减小为109．2 m。心墙仍承担绝大部分水头，其承担的最大比降将从2．50增大至3．61，反滤层Ⅰ的最大水平比降从0．22增大到0．29，心墙后反滤层Ⅰ的自由面高程从2 084．81 m升高至2 086．97 m。

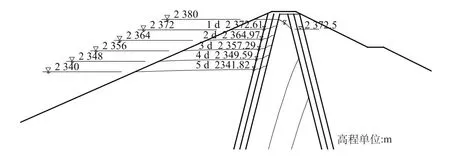
图4 库水位下降上游坝体非稳定渗流计算结果Fig．4 Phreatic surface of unsteady seepage computation during decline of reservoir water level

3．2 非稳定渗流计算成果分析

上游坝体非稳定渗流计算浸润线见表5。图4给出了库水位下降前的坝体浸润线和等势线及水位下降过程中上游坝体内的浸润线变化情况。从计算结果可以看出，上游坝体浸润线随库水位的下降而同步下降，上游坝体内浸润线与库水位最大高差为1．82 m，对应于库水位连续下降5 d时的结果。这表明，在库水位连续5 d以8 m／d速度下降的情况下，上游坝壳内的浸润线下降虽有一定滞后，但不是很严重。

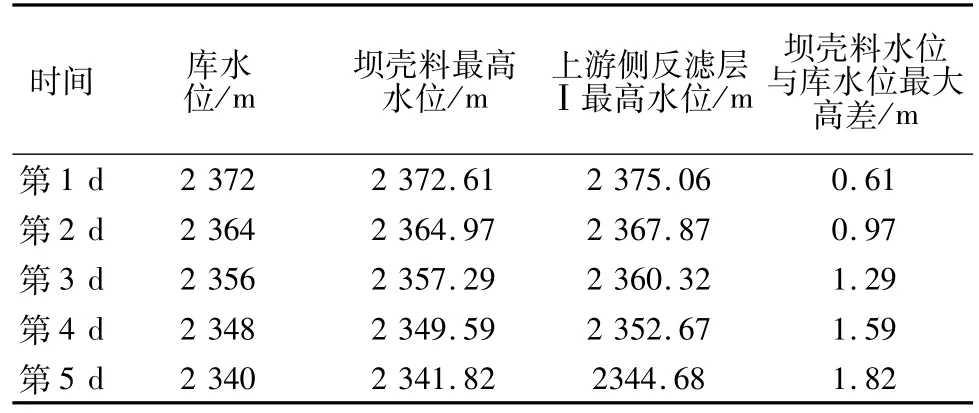
表5 非稳定渗流计算浸润线结果Table 5 Phreatic surface under simulating cases of unsteady seepage field

4 结 论

（1）在拟定的渗透系数、水位和心墙坡比等条件的变化范围内，稳定渗流条件下心墙下游坝壳料中的比降都低于0．01，库水位大幅度下降时上游坝壳内的自由面几乎同步下降，说明坝壳内的渗流场分布有利于渗透稳定和坝坡稳定。

（2）当反滤层Ⅰ与心墙渗透性差别不大时，大坝分区类似于反滤层Ⅱ单层反滤，对反滤层Ⅱ的设计要求必须非常严格。当心墙渗透性与反滤Ⅰ区相差10倍以上时，心墙承担97%以上的水头损失，大坝分区和渗流场分布比较合理。

（3）维持心墙顶宽6 m不变，心墙坡比为1∶0．25时，心墙承担的最大比降小于根据试验成果取得的允许比降值。当两侧坡比为1∶0．2和1∶0．15时，心墙承担的最大比降可能会超过允许比降值，渗透稳定性将更加依赖于反滤层的保护作用。

（4）校核水位条件下，上、下游水头差比设计水位条件下低约20 m，下游水位相应抬高约20 m，坝体渗流场除心墙下游各分区内自由面有相应幅度抬升而外，其他变化不大。

（5）日冕心墙坝渗流场的分析成果为工程预可研提供了设计依据。下阶段进一步的分析工作还必须建立在更丰富的试验资料基础上，并考虑坝基渗流场和帷幕的作用。关于坝肩绕渗及心墙局部缺损的影响还有待采用三维模型进行分析。

［1］ SL274－2001，碾压式土石坝设计规范［S］．

［2］ 保华富，张永全，忱 蓉，等．掺砾风化料作为高坝心墙防渗体的试验研究［J］．水利与建筑工程学报，2008，6（1）：34－37．

［3］ 谢正明，邓 军．糯扎渡水电站防渗土料抗渗透变形试验研究［J］．云南水力发电，2003，（1）：30－32．

［4］ 饶锡保．清江水布垭水利枢纽砾石土和风化页岩料作高心墙堆石坝防渗材料的研究阶段报告［R］．武汉：长江科学院，1997．

［5］ 长江科学院水利部岩土力学与工程重点实验室．瀑布沟水电站心墙砾石土碾压试验报告［R］．武汉：长江科学院，2007．

［6］ 杜明祝，郑爱国．瀑布沟水电站高土石坝心墙防渗料的工程地质特性评价［J］．四川水力发电，1993，（4）：24－29．

［7］ 雷泽宏．瀑布沟水电站心墙防渗料工程性质研究［J］．四川水力发电，1994，12（4）：43－50，87．

［8］ 雷泽宏．瀑布沟水电站心墙砾质防渗料防渗与抗渗性能研究［J］．四川水力发电，1995，1（1）：27－31．

［9］ 吕 衡，李小泉．瀑布沟工程宽级配砾石土抗渗性能改善试验研究［J］．四川水力发电，1996，6（2）：45－50．

［10］沈宝玉．瀑布沟水电站高土石坝宽级配砾石土防渗性能研究［J］．四川水力发电，1995，6（2）：42－46．

［11］陈定贤，袁光国，吕 衡，等．瀑布沟电站防渗土料的研究［J］．四川水力发电，1995，6（2）：51－56．

［12］陈伟群，刘路平，陈霞林．泸定水电站工程监理的重点与难点［J］．中南水力发电，2006，9（3）：49－51．

［13］段祥宝，李祖贻．瀑布沟水电站大坝三维渗流数值模拟研究［J］．水电站设计，1997，13（1）：29－38．

［14］谢 红，张家发，吴昌瑜，等．水布垭水利枢纽三维渗流场有限元分析［R］．武汉：长江科学院，1999．

［15］张世泉．张峰水库大坝渗流及稳定设计［J］．山西水利，2007，（4）：107－108．

［16］李思慎，谢 红．丹江口左联土石坝渗流问题研究［J］．水利水电技术，1994，（7）：57－61．