浅析计算机科学与技术专业中“离散数学”教学方法的改进

仇利克 赵 静 赵扬帆

摘要:“离散数学”是计算机科学与技术专业必修的专业基础课程,学好该课程对于学习计算机专业的其他课程以及培养学生抽象思维能力和解决问题的能力十分重要。本文阐述如何培养学生学习离散数学的兴趣,强调了离散数学理论应该与计算机中的应用相结合,并从多方面对离散数学教学方法的改进进行分析和探讨。

关键词:离散数学;教学方法;计算机

中图分类号:G642 文献标识码:A

“离散数学”作为计算机科学与技术专业必修的专业基础课,在计算机领域有着广泛的应用。它提供了许多计算机专业课程的数学基础,这些课程包括数据结构、算法与分析、数据库理论、自动化理论和操作系统等。学好离散数学,一方面可以为后续的课程打下基础;另一方面,通过学习离散数学,可以培养学生的抽象思维和逻辑推理能力,提高发现问题、分析问题和解决问题的能力,为今后的学习和工作打下坚实的数学基础。但由于该课程具有概念多、理论性强、高度抽象、枯燥等特点,致使在教学中出现很多问题。比如,学生学习积极性不高,学生单一的把该课程看作是一门与计算机毫无关系的数学课程来学,对该课程在计算机领域的作用认识模糊等,导致教学效果不理想。因此,激发学生对该课程的学习兴趣,改进离散数学的教学方法是十分必要的。

1培养学生的兴趣

在任何一门课程的讲授中,培养学生的学习兴趣都是非常重要的。

为了培养学生学习离散数学的兴趣,在教学中要特别注重前几堂课的教学,尤其是第一堂课,不能直接进入离散数学的理论知识学习,而是要通过一些实例来说明离散数学的用处,如“哥尼斯堡七桥问题”、“四色问题”等。通过前几堂课的教学,让学生充分认识到离散数学与计算机科学其他课程之间的密切关系,从而从思想的高度认识此门课程的关键性。

当然,教师课堂教学的艺术性与感染力也是培养学生对离散数学产生兴趣的重要方面。因为大部分学生对离散数学这门课程的地位和作用认识不足,学习兴趣没有学习与编程语言相关的课程那么高涨,上课容易走神,从而导致最终的考试结果不理想。教师除了对这门课程内容要熟练掌握外,还要提高自己的教学艺术水平,正确运用多种手段来吸引学生的注意力,充分发挥教师的主导作用,驾驭好课堂时间,增强课堂教学的艺术性和感染力,也可适当制作一些动画和图形避免视觉疲劳,达到让学生主动学习这门课程的目的。

2注重离散数学理论与它在计算机中的应用相结合

在“离散数学”课程的教学过程中,我们应该理论联系实际,注重它在计算机学科中的应用,来提高学生学习的兴趣和对该课程的重视。

数理逻辑是所有数学推理的基础,在人工智能、程序理论和数据库理论等的研究中有着实际的应用,如专家系统、机器人等都离不开数理逻辑。集合论在计算机科学中也有广泛的应用,它为数据结构和算法分析奠定了数学基础,如在软件工程和数据库中也会用到。抽象代数是关于运算或计算规则的学科,在计算机科学中也有广泛的应用,如形式语言与自动机、密码学、网络与通信理论、程序理论和形式语义学等方面都要用到代数结构的知识,其中格与布尔代数在通信系统中发挥着重要作用。图论在数据结构、操作系统和计算机网络中都有广泛的应用,如数据结构中的图和树都是以图论为基础,网络中的拓扑结构都是用图来表示。

通过这种关联,并对适当的知识点举例说明来加深学生对知识的理解,还应随时介绍所学知识的应用背景和发展方向,使学生能够感受到学习这门课程的必要性,调动学生的积极性。

3注重课堂教学方法的改进

3.1找到结构,克服“散”

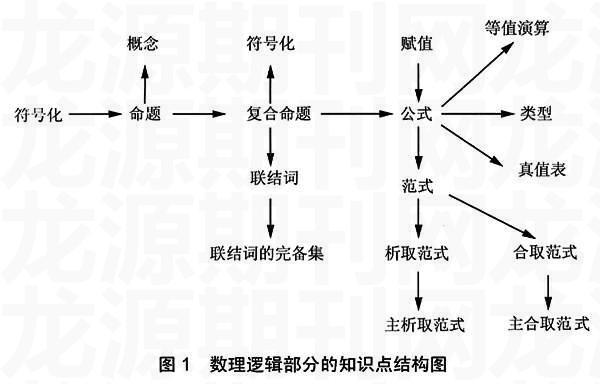
在离散数学中,概念多、理论性强、知识点散,抓不住重、难点,老师讲起来费劲,学生听起来吃力。因此,每节课的内容都要有一条主线,选择本节课要讲的知识点,用一条线将相关的知识点串起来。以命题逻辑为例,可以这样把各知识点串起来,如图1所示:

每个知识单元完成后加以总结,讲出知识点之间的关联结构,达到系统掌握命题逻辑知识的目的。

3.2有取有舍,克服“满”

离散数学的内容太多,若课时有限,那我们要有取有舍,可以选择其中的60%～70%的内容进行讲授,其余留给学生阅读思考或布置作业,这样不仅可以锻炼学生的自学能力,还节省了课堂时间。这就要求我们课堂上一定要把内容讲透,不能蜻蜓点水,除了要讲解基础性知识和本节的重难点外,还要着重培养学生对学科方法的运用以及解决问题的思路,知识点之间的关联也要交代清楚。而对于一些类似的方法或例子、推广的结果、能够自学的知识和某些繁琐的推导要舍得放弃。

例如在讲解代数结构这一部分时,代数系统、群要重点讲授,这是后续内容的基础,环、域和格可以简单讲授,课时少的话可以只把概念讲授清楚,独异点等可以留给学生课下阅读和学习。再如组合数学部分,基本的组合计数、递推方程与生成函数、容斥原理重点讲授,鸽巢原理、Ramsey定理、Polya定理等简单讲授,推广的容斥原理、Ramsey定理的应用、带权的Polya定理留给学生阅读。

掌握好取舍关系,才能让学生把握离散数学的关键点,而不至于偏离方向,不至于丧失学习的信心。

3.3掌握节奏,克服“快”

离散数学概念多,理论性强,学生上课容易走神,开小差,因此课堂上一定要掌握好节奏,给学生喘息和思考的时间,这就要求我们在安排学时时要留有一定的余地。课堂上,对不同内容的讲解要穿插进行,有张有弛,如概念、定理与应用实例可以结合起来讲解,便于学生理解,也可以适当穿插一些解题方法的分析等,也可以在课堂上通过提出一些思考题来放慢节奏,或者是介绍一些历史背景、相应知识点的新进展等。采用适度“慢”策略,是在强调教师的教学目的和方法的同时,更强调学生的独立思考和综合判断能力,因为学生才是学习的主体,教学活动的中心。

3.4启迪思路,克服“灌”

离散数学的教学中,我们要克服“灌”的教学习惯,采用启发式教学。启发是数学教学的灵魂,因为归根结底数学是人类一种高度的精神活动。美国著名数学家柯朗(R•Courant)在《数学是什么》一书中指出,“数学,作为人类思维的表达形式,反映了人们积极进取的意志,缜密周详的推理以及对完美境界的追求。它的基本要求是:逻辑和直观,分析和构造,一般性与个别性。虽然不同传统可以强调不同的侧面,然而这些互相对立的力量的相互作用以及它们综合起来的努力才构成数学科学的生命、用途和高价值。”因而数学教学决不能只告诉学生现成的数学结论,或让他们死记公式定理法则,然而要在很短的时间内让学生理解某些数学理论及逻辑是非常困难的,必须采用启发式教学,让学生运用自己的智力认真思考,这就对数学教师提出了新的要求,其精髓在于“提出问题→讲解方法→推广应用”。首先我们通过列举实例提出问题;然后讲解解决此问题的思路,即建模(利用离散数学中学习的方法和理论来求解);再通过典型实例细述此方法和理论在实际中的应用;最后总结此方法和理论适用的条件及一般化推广。

如在讲“有穷集的计数”这一小节中,我们可以通过列举实例来提出问题,例:求1到1000之间(包含1和1000在内)既不能被5和6,也不能被8整除的数有多少个?我们可以利用“文氏图法”和“包含排斥原理”两种方法来解决这个问题,首先可以通过讲解如何利用“文氏图法”来解决此问题的思路,为后面引出“包含排斥原理”做好铺垫;接着可以引出“包含排斥原理”,并讲解用此原理如何解决上面的问题;最后,总结一下“包含排斥原理”的适用条件以及它的推论。

再如在讲解图论时,我们可以模拟哥尼斯堡七桥问题的实景,通过场景描述对比,让学生明白七桥问题跟桥的长短、岛的大小无关,从而抽象到欧拉图问题,这也就是图论知识的起源,同样的方法可以应用到哈密尔顿图等问题的讨论。

通过这种启发式教学,让学生对所学知识有直观的了解,然后再引导学生自己列举类似问题,进一步加深对有关定义、定理以及推论的理解,提高学生学习的兴趣和增强学生分析问题、解决问题能力的双重目的。

3.5适时地给学生总结

离散数学的内容多而杂,课时少。讲课时,授重点解难点,对于易懂的内容可以一带而过或者留作课下自学。除此之外,课堂小结是一项非常重要的教学技巧与授业解惑利器。鉴于离散数学的抽象性与复杂性,学生课上容易走神,如果上堂课没听好则必然会影响下堂课的听课兴趣和听课质量,因此,进行课堂小结是必要的,起着承上启下的作用。

每次课的最后留下5分钟左右,对本次课所讲的内容进行小结,尤其是重点内容。每次课开始时对上次课讲的内容进行回顾;每章讲完后适当进行小结,总结前后各知识点之间的关联,以及应该掌握的知识点,给学生们一个总体印象,这样有助于学生对知识点的掌握及自我能力的提高,更重要的是给学生足够的信心来学习这门课程,而不至于陷于越学越听不懂,越听不懂越不想学的恶性循环。

4结语

由于在计算机科学领域中很多地方都采用了离散数学的概念思想和方法,因此离散数学已经成为计算机科学与技术专业学生必须掌握的理论基础和数学工具。本文从计算机科学与技术专业学生学习离散数学的角度论述怎样激发学生学习的积极性及学习兴趣,注重与计算机学科的结合及注重课堂教学方法的改进等方面探讨了“离散数学”课程教学方法的改进。

为了提高这门课程的教学效果,还可以研究怎样更好地利用多媒体创造良好的学习环境,提高课堂效果,以及如何在该门课程中引入实践课,让学生能将所学的知识应用于实践,提高他们的创新精神。我们还可研究怎样建立该课程的教学网站,补充、整合离散数学的教学资源及网上答疑和讨论,方便学生课外进一步学习。

参考文献:

[1] Rosen K H. 离散数学及其应用[M]. 袁崇义,屈婉玲,译. 北京:机械工业出版社,2002.

[2] 王元元,张桂芸. 离散数学导论[M]. 北京:科学出版社,2002.

[3] 屈婉玲,耿素云,张立昂. 离散数学[M]. 北京:高等教育出版社,2008

Analysis of Computer Science and Technology of “Discrete Mathematics” to Improve Teaching Methods

QIU Li-ke, ZHAO Jing, ZHAO Yang-fan

(Qingdao College, Ocean University of China, Qindao 266300, China)

Abstract: The discrete mathematics is the computer science and the technical specialized compulsory specialized foundation curriculum. It is extremely important to learn this curriculum regarding to study the computer specialized other curricula as well as to raise the student abstract thinking ability and solves the question ability. This article elaborated how to trains the interest of the student to study the discrete mathematics, emphasized the discrete mathematics theory should unify with the computer in application, and has carried on the analysis and the discussion from the multi-aspects to the discrete mathematics teaching method improvement.

Key words: Discrete Mathematics; teaching method; computer