空化对流体管路瞬态特性影响分析

赵春章，李 永，潘海林，魏延明

（北京控制工程研究所，北京100190）

空化对流体管路瞬态特性影响分析

赵春章，李 永，潘海林，魏延明

（北京控制工程研究所，北京100190）

空化（或称气穴）是流体系统中常见的现象，它显著地影响着流体管路的瞬态特性。考虑气体在液体工作介质中溶解和析出以及液体介质自身气化，建立相应的流体属性模型，计算不同压力下流体的等效密度及体积模量；同时以一维管道瞬变流理论为基础，考虑流体系统中的空化及气泡溃灭，采用有限差分法计算流体管路锤击过程中的压力脉动。求得的结果与真实物理现象较为接近，能够为流体系统的设计提供依据和参考。

空化；流体系统；瞬态特性

1 概 述

以液体作为工作介质的流体系统中通常会含有少量的气体，例如液压系统液压油中混有空气，航天器推进系统推进剂中含有挤压气体，这些气体或溶于液体介质或析出以气泡的形式存在。在高压时，气体溶于液体介质，在压力降低时达到一定真空度时便会出现过饱和现象，并开始逐渐析出气体。当局部压力变化到“气体分离压”时，液体介质内溶解的气体会大量分离出来，成为气泡而产生空穴现象。在高压作用下，气泡就会被挤压破裂，体积迅速缩小，在系统管路或其它局部范围内产生幅值很大的高频冲击压力，从而使管路产生剧烈振动，激发出高频噪声。此外当系统的压力低于液体介质的饱和蒸气压时，便会产生液体介质自身气化现象，相比气体的析出，液体介质的气化过程要快得多，这些现象可以统称为空化。在流体系统工作时，阀门突然关闭的情况下，会在管路中形成锤击，本文针对空化这一现象，调整相应的空化状态下流体属性，并对这一过程进行仿真，分析了空化对流体系统锤击瞬态特性和压力波传播速度的影响。

2 理论模型

2.1 管路内液体瞬变流方程

假设管流是一维绝热有摩擦的液体瞬变流，连续方程和运动方程为［1-2］

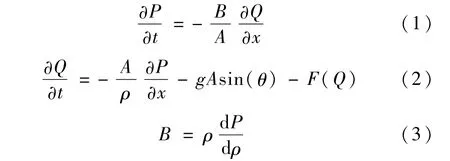
其中，A为流体管路截面积，P为流体压力，Q为流体流量，B为管流流体的等效体积模量，F（Q）为管壁的摩擦流阻项，ρ为等效密度。

2.2 流体属性

流体属性如密度、粘性、体积模量是流体系统仿真中最基本的内容。气体从流体介质中析出和流体介质本身气化对流体系统动特性影响主要表现在等效密度和等效体积模量的变化。

在实际的流体系统中，液体工作介质中通常会包含部分气体，气体可能溶于液体介质或以气泡的形式存在，假设将溶于液体介质中的气体分离出来并与液体介质同时处于温度为273 K，大气压力为1个大气压的环境下，设液体介质和气体的体积分别为Vlid和Vgas，相应的气体体积分数定义为注.气体体积分数x对应1大气压和273 K温度下的数值。

液体工作介质溶解气体的体积分数遵循Henrry定律，取一最低压力点，当系统压力高于这一值时，所有气体完全溶于液体。这一压力点称为“分离压力”。

定义“气体分离压”为 Psat，当系统压力大于此值时，所有的气体将溶于液体介质，当系统的压力小于此值时，一些气体析出，剩下的一些气体则溶解于液体介质。因为气体的析出过程是一个相对缓慢的过程，对于一个相对稳定的流体系统，Psat的取值为实际压力值。对于一个类似射流系统这种高速流体系统，即使压力极速增高，气体并没有充足的时间溶于液体，可以将Psat设为一个较高的值，以保证在进行数值仿真时，液体中含有相应的气体与物理实际保持一致。

当压力继续降低时，溶于液体介质的气体会全部析出，同时液体本身会产生气化现象。一般来说，液体不是完全纯净的介质，液体的气化过程发生在一定的压力范围内，把液体气化的起始点定义为，液体全部气化的完成点定义为。

1）P≥Psat：没有气化蒸气，同时气体溶于液体工作介质；

根据式（3）系统等效体积模量的定义，反过来我们可以由参考压力为Pref时的密度 ρ（Pref，T）得到在压力为P、温度为T时的密度

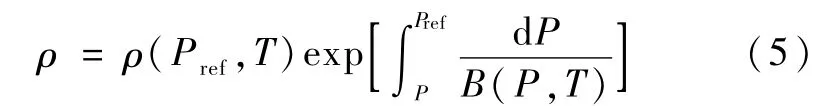
只要确定等效密度和体积模量这两个变量中的一个变量，就可以根据公式得到另外一个变量。这里的等效密度和等效体积模量是指假设气体在每个单元内均匀分布的情况下的气液混合物的密度和体积模量。

不同压力，等效密度和等效体积模量计算如下：

1）P≥Psat

此时气体全部溶于液体，液体的体积模量不受气体体积分数的影响。与流体工作介质相比，溶解的气体质量非常小，但为了保证流体质量守恒，要把它计算在内。对于给定的压力P和温度T，流体混合物的密度为

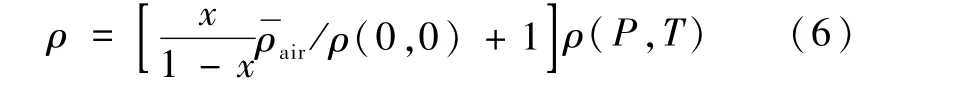
如果液体体积模量为一常数，则

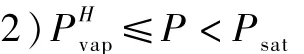
此时气体部分溶于液体工作介质，部分呈自由状态。定义溶解气体的体积分数

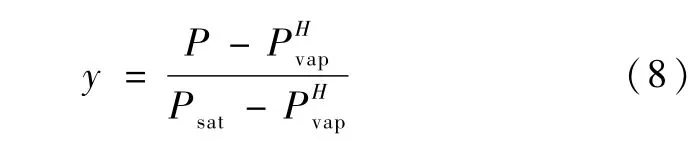
根据Henrry定律，未溶解气体的体积分数θ应为（1-y），但此状态为平衡状态，并不能瞬时转变。为了保证曲线与上一工况的平滑过渡，定义θ为

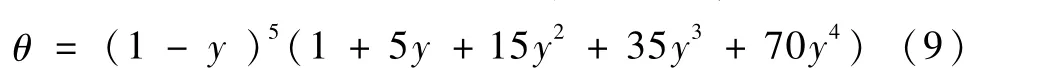
混合物的密度为

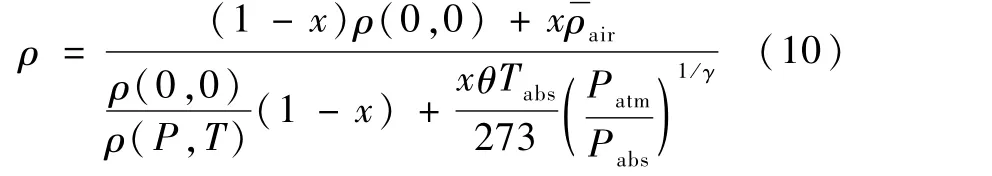
式中，Tabs为流体绝对温度，Patm为标准大气压，Pabs为流体绝对压力，γ为气体多变指数。

如果液体介质体积模量为常数，则

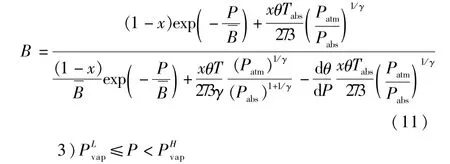
定义φ=φ（P）为液体工作介质气化的质量分数，有

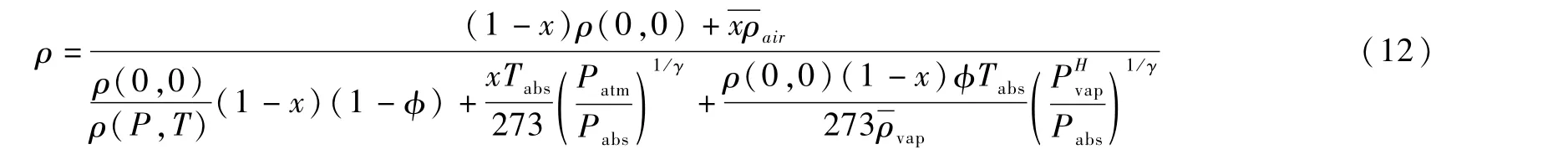
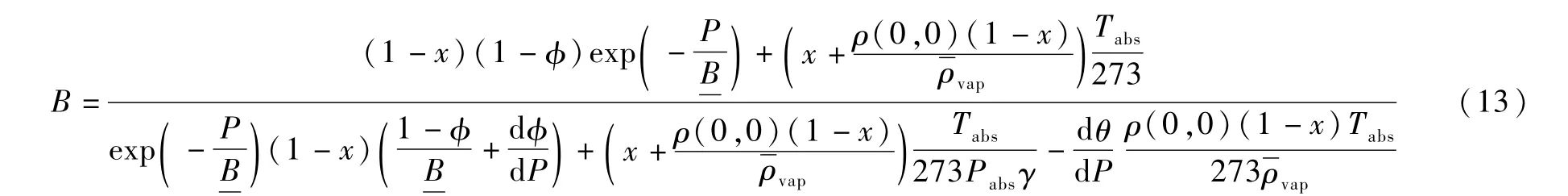
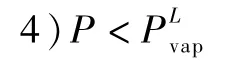
此工况相当于工况3的特殊形式。

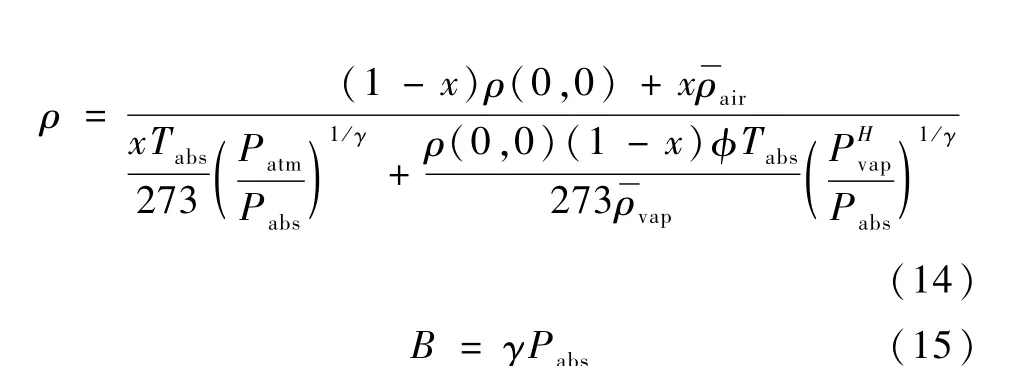
假设在常压（1个大气压）下，液体的密度为1 000 kg/m3，体积模量为1 700 MPa，气体体积分数为0.1%，最高饱和蒸气压为0.5 MPa，最低饱和蒸气压为0.6 MPa。在不同压力下流体等效密度、体积模量及声速变化如图1所示。可以看到，流体在低压段刚性急剧降低，可压缩性明显变强。

3 方程仿真求解

分析管路瞬态特性的参数分布模型有集中参数模型、分布参数模型等。集中参数模型求解简单但不够准确，这里采用分布参数模型。数学方程的离散化方法有特征线法、有限差分法和有限元法等。若采用特征线法在分析较复杂的含气泡和气穴的管路动态特性时，难以捕捉到参数间断效应。本文采用有限差分法离散方程组空间项，时间项迭代采用传统的线性多步法。

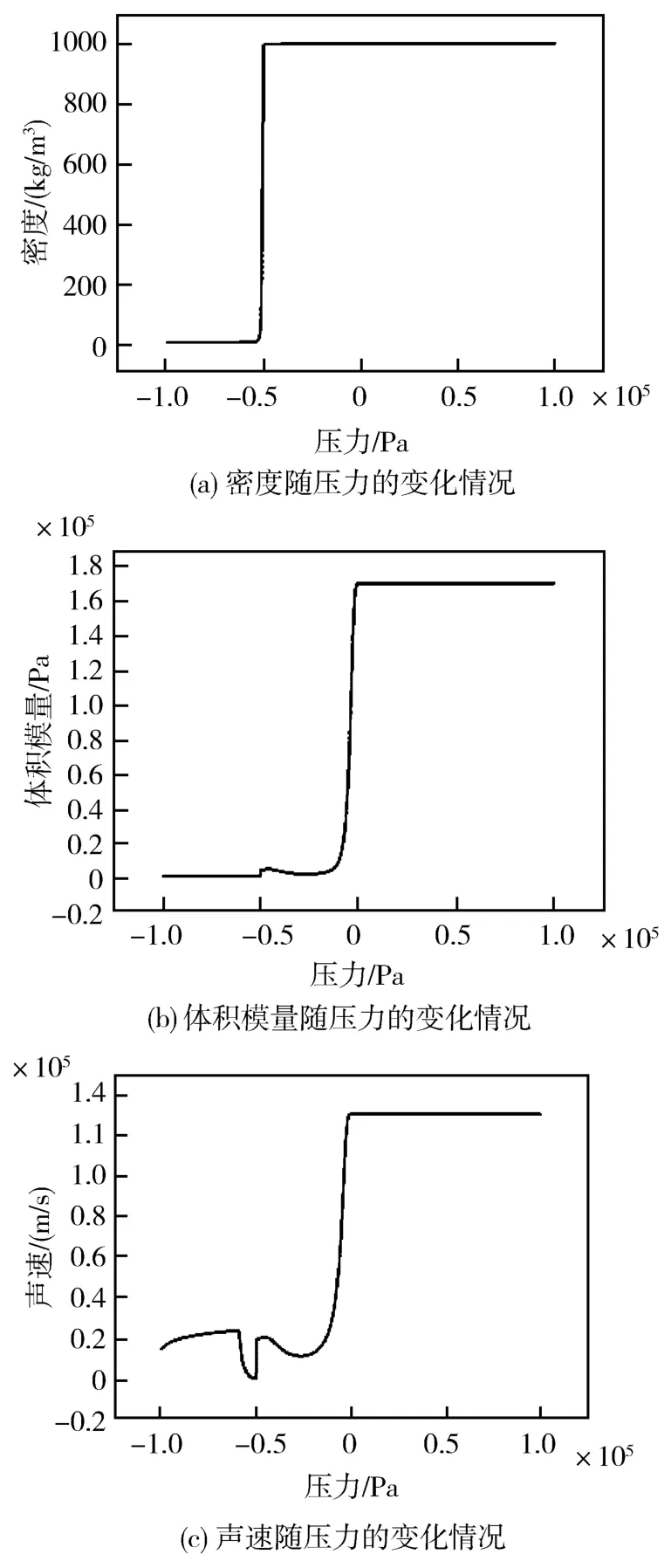
图1 不同压力下流体属性变化

4 算例及结果分析

以一段连接两个容器的管路为研究对象，如图2所示。

假设管路中存在稳态的初始流动，当管路的阀门突然关闭时，管路中液体的动能和压力能之间的相互转换将引起压力脉动。分析阀门和容器之间的被考察管路的动态特性。

仿真参数如下：阀端压力为3 MPa，容器端压力为2 MPa，管半径为4 mm，管长为20 m。

假设在常压下（1大气压）液体工作介质的密度为1 000 kg/m3，体积模量为1 700 MPa。不考虑空化，得到靠近阀端第一个内点的压力脉动曲线，如图3所示。

考虑空化特性的压力脉动曲线与不考虑空化特性的压力脉动曲线对比图如图4所示。

图2 流体系统示意图

由图4可见，当不考虑液体介质的溶气和气化特性时，压力脉动曲线会出现绝对压力小于0的现象，这种现象违背实际情况。当考虑液体介质的溶气和气化特性时，可以看到，空化不仅对压力脉动的低压区产生影响，由于空化引起的流体压缩性的变化还会激发压力上升阶段的高频震荡。

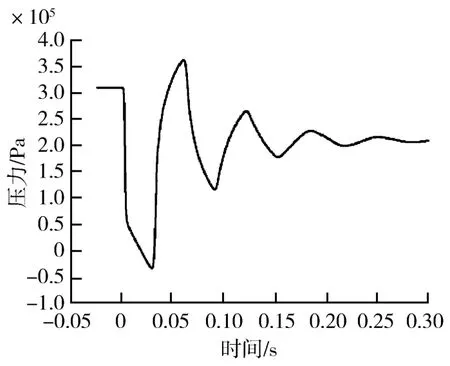
图3 不考虑空化的压力脉动曲线

4 结 论

与不考虑空化的流体模型相比，考虑空化的模型在低压区能较好地符合实际情况。采用考虑空化的计算模型能够捕捉到由于空化产生的高频震荡，其计算结果能够为流体系统的设计提供依据和参考。

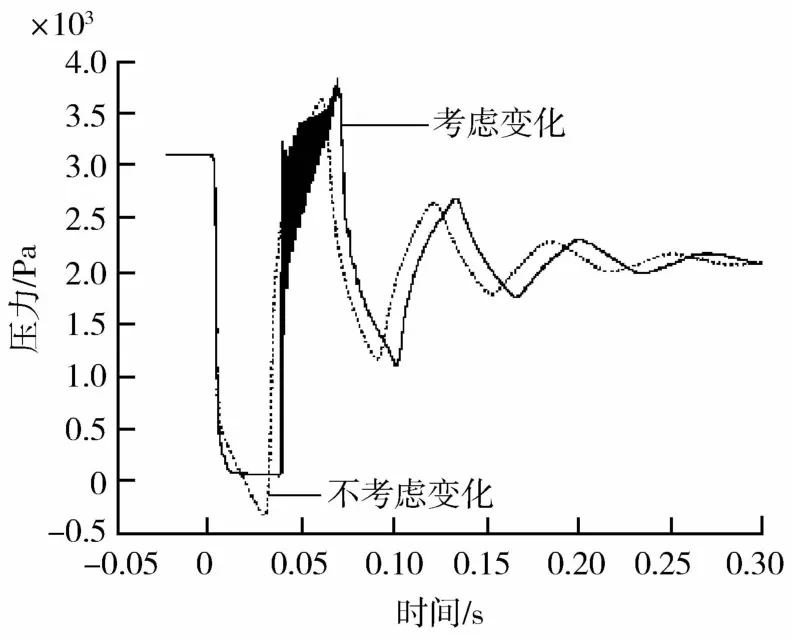
图4 两种情况下的压力脉动曲线对比图

［1］ Pu J N.Analysis and control of water hammer in pipeline［M］.Beijing：China Machine Press，1991

［2］ Wylie E B，Streeter V L.Fluid transients［M］.M ichigan：FEB Press，1983

Effect of Cavitation on the Transient Characteristics of Fluid Pipeline

ZHAO Chunzhang，Li Yong，PAN Hailin，WEIYanming
（Beijing Institute of Control Engineering，Beijing 100190，China）

Cavitation is a general phenomenon in fluid systems.It has an obvious effect on the transient characteristics of the fluid system.Cavitation model is taken into account for simulation of fluid systems，fluid properties such as density and bulk modulus are calculated in different pressures.The analyticalmodels are developed by using the hammer and one-dimension fluid transient theory based on the finite difference method，in consideration of the cavitation，release and collapse of bubbles.The results are much closer to the actual physical process and provide guidance and reference for the design of fluid systems.

cavitation；fluid system；transient characteristics

O427.4，TP271

A

1674-1579（2008）03-0061-04

2008-01-03

潘海林（1960-），男，四川人，研究员，研究方向为航天器推进技术（e-mail：panhl@bice.org.cn）。