多体航天器大角度机动鲁棒控制
袁长清,李俊峰,沈 英,2
(1.清华大学航天航空学院,北京 100084;2.空军长春航空大学,长春 130022)
多体航天器大角度机动鲁棒控制
袁长清1,李俊峰1,沈 英1,2
(1.清华大学航天航空学院,北京 100084;2.空军长春航空大学,长春 130022)
研究了具有模型不确定性的多体航天器大角度机动控制问题。航天器姿态动力学方程具有不确定性和非线性。首先通过逆系统方法求得近似伪线性系统,然后应用H∞混合灵敏度方法和μ综合方法设计了两种鲁棒控制器。通过引入PD控制器,避免了H∞控制器设计时方程出现奇异。针对航天器中心体与天线同时跟踪不同目标的任务,进行了数值仿真。仿真结果表明在同等条件下两种鲁棒控制器都能满足鲁棒稳定性指标,其中μ控制器的鲁棒性能更好。
多体航天器;H∞控制;μ综合;大角度机动
1 引 言
大角度机动作为现代航天器姿态控制关键技术之一,一直为航天控制领域所关注。国内外许多学者对航天器大角度姿态机动问题进行了广泛研究[1-4]。航天器快速大角度机动会引起动力学方程高度非线性。现代航天器的复杂结构,也使得精确建模非常困难。在轨航天器不可避免地受到气动力矩、太阳光压、重力梯度力矩和地磁力矩等环境力矩的干扰。所有这些因素都对航天器控制系统的鲁棒性提出了更高要求。
目前应用于航天器的非线性控制方法,比如非线性滑动模态控制器[5]、基于Lyapunov方法的非线性姿态控制[6]和模糊滑模控制[7]等,均在一定程度上依赖于被控对象模型,当模型比较复杂、参数变化较大时,均受到一定的限制。逆系统方法[8]是一种常用的非线性控制方法,但它要求建立精确动力学模型。经典线性鲁棒控制理论发展至今已经比较成熟,能较好处理线性或弱非线性对象的鲁棒控制问题,但不能处理高度非线性对象。本文针对多体航天器大角度机动问题,将逆系统方法与H∞混合灵敏度方法和μ综合方法结合,设计了两种非线性的姿态机动鲁棒控制器。引入PD控制器,避免了H∞混合灵敏度设计时方程出现奇异,方便控制器设计。

图1 多体航天器
2 航天器姿态动力学方程
航天器由中心刚体和一个快速机动天线组成。参考坐标系定义如图1所示,其中OXYZ、OoXoYoZo、ObXbYbZb和OaXaXaZa分别为地心惯性系、轨道坐标系、中心体固连坐标系和天线固连坐标系。考虑航天器在俯仰平面(OoXoZo平面)内运动的特殊情形,此时系统姿态运动仅限于俯仰面内,包括中心体绕俯仰轴的转动和天线绕Ya轴的转动,则航天器的动力学方程为

式中 x=[θ1θ2]T,Tc=[TbTa]T,其中 θ1、θ2分别为中心体相对惯性系的姿态角和天线相对中心体的转角,Tb、Ta分别为中心体和天线的控制力矩,方程中各项具体形式见附录一。
在工程中,由于受到弹性结构、液体燃料和太阳帆板方位变化等因素影响,航天器参数存在摄动。因此,将航天器中心体、天线的转动惯量和中心体的质量重新描述为

其中,下标“0”表示标称值,ΔJb和 ΔJa分别表示中心体和天线转动惯量的摄动部分,Δmb表示中心体质量的摄动部分。令 m0=ma+mb0+md,λ10=ma/m0,λ20=md/m0,则

由此可得

其中,
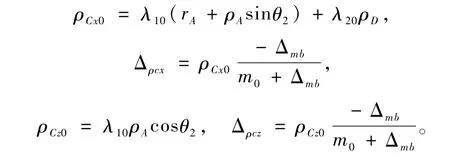
因此,具有不确定性的动力学方程可以描述为
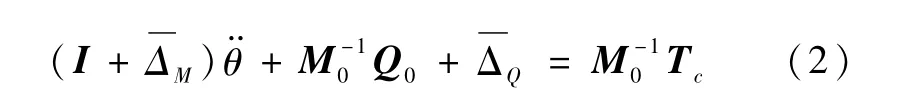
其中

3 鲁棒控制器设计
由于方程(2)较为复杂,首先对参数摄动系统(2)应用逆系统方法,得到近似伪线性系统,并将其转化为系统模型。然后,应用H∞混合灵敏度和μ综合方法设计两种鲁棒控制器。
3.1 近似伪线性系统
逆系统方法[8]是一种有效的非线性控制方法,物理概念清晰、设计简便。基本思路是先求出α阶积分逆系统,然后将其串连在原系统之前,得到的组合系统即为相应的近似伪线性系统。根据方程(2),利用逆系统方法,可以求得标称参数下的逆系统如下

为了实现姿态跟踪,辅助变量δ被设计成如下形式
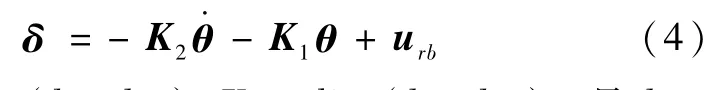
其中,K1=diag(k11,k12)、K2=diag(k21,k22),且 k11,k12,k21和 k22为正实数,urb为下一节要设计的鲁棒控制器。将式(4)代到式(3)中,则逆系统控制器设计如下
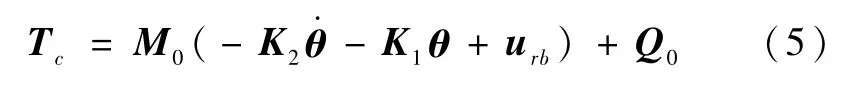
将方程(5)代入式(2),可得
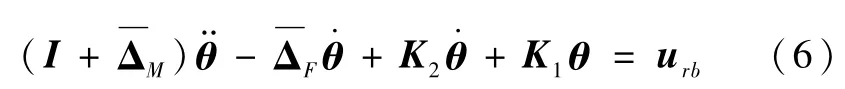
在H∞混合灵敏度问题中,如果增广系统有虚轴上的极点或零点,此时求解方程会产生奇异。应用双线性变换可以解决上述问题,但采用双线性设计时,参数不便于调整。因此,这里通过引入PD控制器(含K1和K2两个参数矩阵),参数调整灵活,便于控制器设计。下面推导系统模型。
3.2 系统模型
假设参数摄动满足如下有界条件
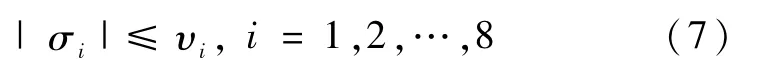
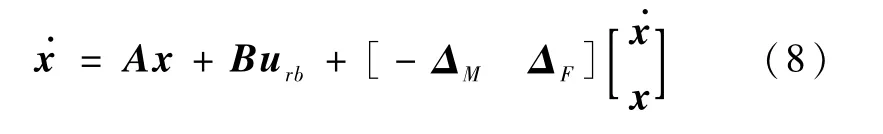
其中,


对式(8)右端第三项系数矩阵做最大秩分解可得
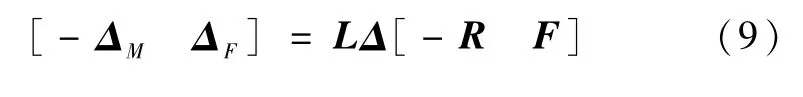
其中,

将式(9)代入式(8)中,得
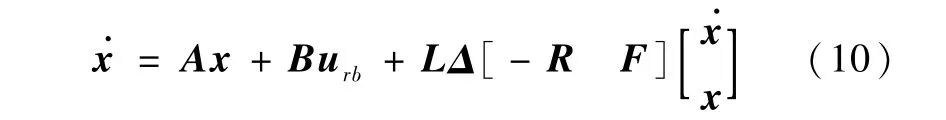
定义z和w为Δ的输入和输出,即w=Δz,
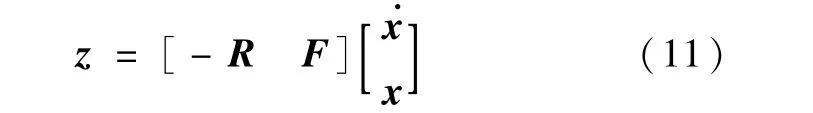
代入式(10)中,得到

其中

式(12)、(13)和(14)描述的模型为系统模型 G,如图2所示。d为干扰与测量噪声,urb为控制输入,y为系统输出。下面将针对参数摄动系统模型G,设计鲁棒控制器。

图2 系统模型
3.3 鲁棒控制器设计
为实现鲁棒性能指标,G的闭环系统需满足如下性能指标[9]:
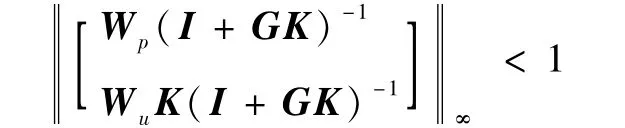
Wp(s)是为抑制干扰、实现优良的瞬态响应,Wu(s)为控制输入加权矩阵。H∞次优控制器的设计可简要描述为:寻找稳定控制器K使闭环系统传递函数的H∞范数小于给定的正数,即

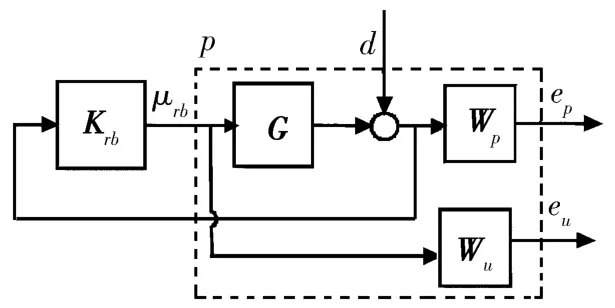
图3 H∞控制器设计框图
3.4 综合鲁棒控制器设计
在实际航天器系统中,摄动全部集中在一处的情况比较少见,通常分散在几处,如果忽略其结构特性,采用 H∞方法设计控制器,会得到保守的结果。下面采用结构奇异值μ定量地表征结构化不确定性对近似伪线性系统稳定性及性能的影响。如图4所示,传递函数矩阵M为广义标称系统,是G0和K的下线性分式变换,即
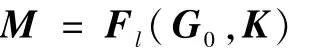
设

鲁棒性能的综合问题可归结为寻找一个稳定化控制器 K,使

图4 μ控制器设计框架

这就是μ综合问题[9]。通常可通过选择一个标度矩阵D来进行计算,因而μ综合问题变成


通常采用D-K迭代法[9],可以求解μ综合问题。
4 仿真结果
下面考虑中心体与天线惯量变化的情况,针对中心体和天线同时跟踪不同目标的任务,分别应用两种鲁棒控制器进行数值仿真。航天器的模型参数如表1所示。Jb、Ja和mb的最大摄动幅度为
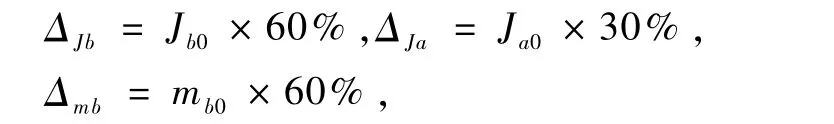
逆系统控制器中的参数取为
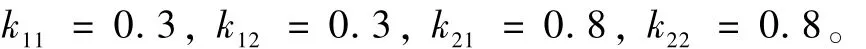

表1 航天器模型参数
采用文献[10]的方法,经多次仿真,选择以下加权函数矩阵
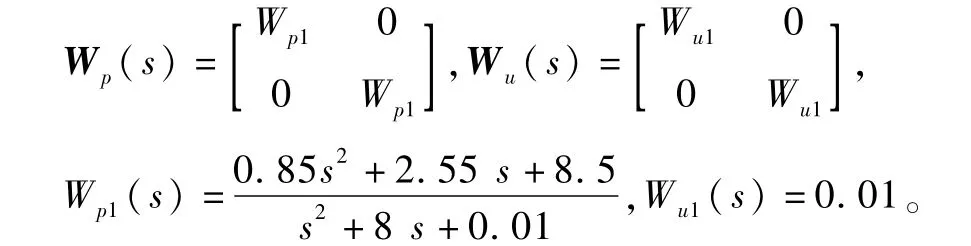
(1)H∞次优控制器
应用matlab鲁棒工具箱的“hinfsyn”函数求解,经过降阶处理,得到8阶鲁棒器。当中心体和天线同时大角度机动时,标称模型情况的仿真结果如图5所示。考虑模型参数摄动的情况,选择10种参数摄动值进行仿真,中心体和天线的仿真结果如图7所示。从仿真结果可知,标称模型情况下,能实现设计性能指标。但当模型参数发生摄动时,虽然闭环系统仍然是稳定的,但控制性能并不优良。
(2)μ控制器
应用matlab鲁棒工具箱的“dkitopt”函数求解,迭代计算三次,结果如表2所示。经过降阶处理,得到8阶鲁棒控制器。当中心体和天线同时大角度机动时,标称模型情况的仿真结果如图6所示。考虑模型参数摄动的情况,选择10种参数摄动值进行仿真,中心体和天线的仿真结果如图8所示。从仿真结果可知,标称情况和参数摄动情况都能实现设计性能指标。
(3)两种控制器的比较
稳定性是控制系统的基本要求,我们更感兴趣的是控制系统的性能。应用结构奇异值μ,可以用一个统一框架来进行系统鲁棒稳定性和鲁棒性能分析。关于鲁棒稳定性和鲁棒性能相关定义和定理见文献[11]。应用matlab鲁棒工具箱的“mussv”函数分析了两种控制器的鲁棒稳定性和鲁棒性能。闭环系统结构奇异值 μΔ[Fl(G,K)]的频率响应如图9所示。在频带0.8~5 rad/s上,μ控制器的鲁棒稳定性要高于H∞控制器;在高频带,两种控制器鲁棒稳定性相当。闭环系统结构奇异值 μΔp[Fl(G,K)]的频率响应如图10所示。μ控制器在规定频带内完全实现鲁棒性能(μ<1),而H∞控制器在某些频带未满足指定的鲁棒性能要求。由于μ综合方法考虑了摄动的结构特性,从而降低了控制器的保守性。

表2 D-K迭代
5 结 论
本文研究了航天器姿态机动鲁棒控制问题。将逆系统方法分别与H∞控制方法和μ综合方法相结合,设计了两种鲁棒控制器。通过引入PD控制器,避免了H∞控制设计时方程出现奇异。与一般的双线性变换处理方法相比,PD控制器参数更方便调节,增加了控制器的设计灵活性。考虑航天器惯量不确定的情况,针对航天器中心体与天线同时跟踪不同目标的任务进行了数值仿真。仿真结果表明两种鲁棒控制器在同等条件下都能满足鲁棒稳定性指标,但μ控制器的鲁棒性能更好。控制器的设计是分步进行的,思路清晰,过程简单,充分利用matlab鲁棒工具箱,降低了控制器设计的工作量,便于工程应用,可以用于更复杂的模型,比如空间机械臂、柔性多体航天器等。

图5 H∞控制器(标称情况)

图6 μ控制器(标称情况)
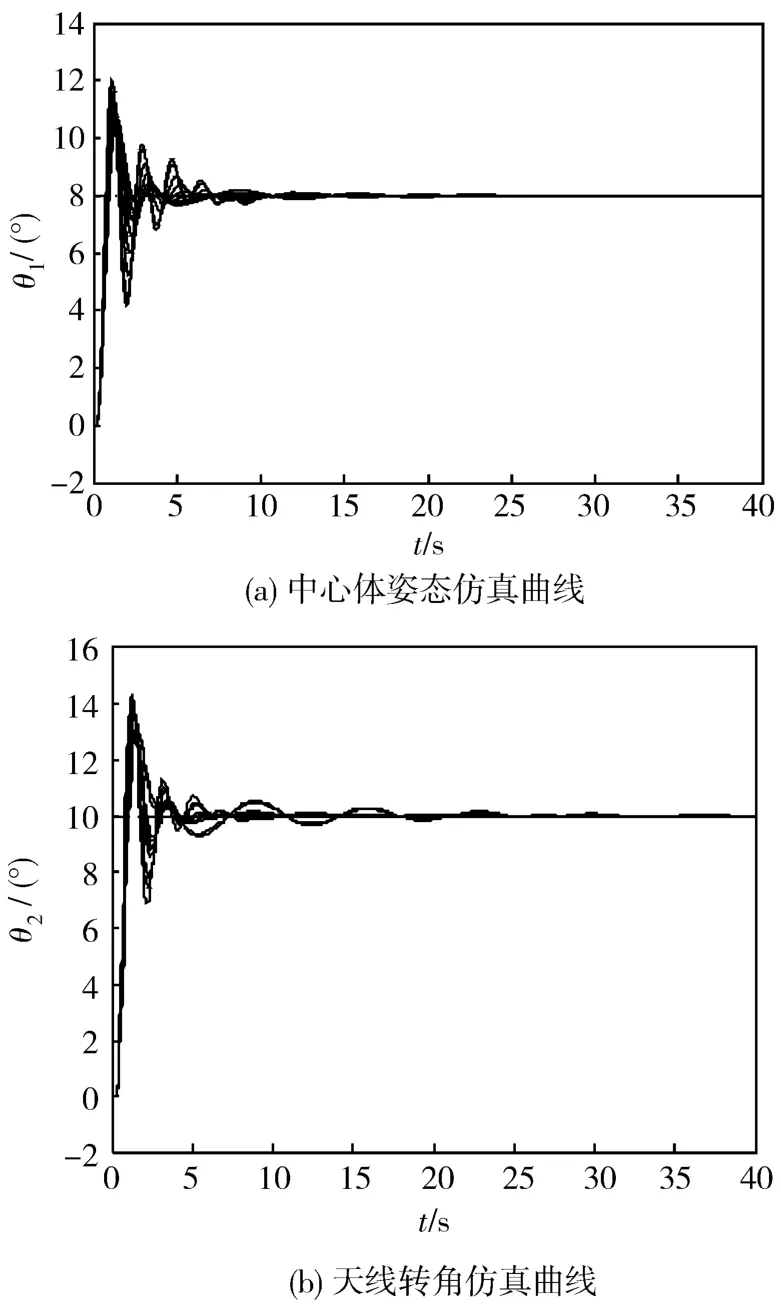
图7 H∞控制器(参数摄动)

图8 μ控制器(参数摄动)

图9 鲁棒稳定性比较

图10 鲁棒性能比较
[1] 周连文,周军,李卫华.挠性航天器大角度机动的滑模变结构控制[J].飞行力学,2004,22(1):71-73
[2] 徐世杰.基于Lyapunov方法的空间飞行器大角度姿态机动控制[J].宇航学报,2001,22(4):95-99
[3] Laia L C, Yangb C C, Wu C J.Time-optimal maneuvering control of a rigid spacecraft[J].Acta Astronautica,2007,60(10):791-800
[4] Banga H,Hab C K,Kimc J H.Flexible spacecraft attitude maneuver by application of sliding mode control[J].Acta Astronautica,2005,57(11):841-850
[5] Cheon Y J,Keum JH,Sim E S.Sliding mode control of spacecraft with actuator dynam ics[C].Int Conf on Control,Automation and Systems,Jeju,Korea,2001
[6] 张景瑞,李俊峰.基于Lyapunov方法的卫星非线性姿态控制[J].清华大学学报(自然科学版),2004,44(5):24-26
[7] 黄显林,王海滨.空间飞行器基于模糊逻辑的连续滑模控制[J].宇航学报,1999,20(3):22-27
[8] 李春文,冯元琨.多变量非线性控制的逆系统方法[M].北京:清华大学出版社,1991
[9] Gu D W,Petkov P H,Konstantinov MM.Robust control design with matlab[M].London:Springer-Verlag,2005
[10] 吴旭东,解学书.H∞鲁棒控制中的加权矩阵选择[J].清华大学学报(自然科学版),1997,30(1):27-30
[11] 吴敏,桂卫华,何勇.现代鲁棒控制(第二版)[M].长沙:中南大学出版社,2006
附录一 航天器动力学模型的相关参数

其中,

以上各式中其他符号的定义见下表。

航天器动力学模型相关符号定义
Robust Control of Large Angle Maneuver for Mu lti-Body Spacecraft
YUAN Changqing1,LI Junfeng1,SHEN Ying1,2
(1.School of Aerospace,Tsinghua University,Beijing 100084,China;2.Changchun Aviation University of Air Force,Changchun 130022,China)
This paper investigates the robust control of large angle maneuver for the multi-body spacecraft with model uncertainties.A nonlinear dynamicsmodel with uncertainties is considered.An approximate pseudo-linear system is developed by using the inverse system method,and two linear robust controllers are designed through the mixed sensitivity H∞optimization and theμsynthesismethod,respectively.A PD controller is used to elim inate the singularity during them ixed sensitivity H∞optim ization.Numerical examples of the central body and antenna tracking different targets are given.The simulation results demonstrate that both controllers are robust stable,and the robust performance of theμcontroller is better than that of the H∞controller.
multi-body spacecraft;H∞control;μsynthesis;large angle maneuver

V412
A
1674-1579(2008)03-0030-07
2008-03-18
袁长清(1974-),男,吉林人,博士研究生,主要研究方向为多体航天器姿态动力学与控制(e-mail:ycq02@mails.tsinghua.edu.cn)。

