基于分散化预测滤波的故障诊断方法研究*
李 骥
(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京100190)
基于分散化预测滤波的故障诊断方法研究*
李 骥1,2
(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京100190)
针对多故障源系统的故障诊断问题,提出一种采用分散化预测滤波与两种不同类型残差相结合的诊断方法。该方法针对不同类型故障敏感的特点,利用不同类型残差,区分系统组件/执行机构故障和传感器故障;利用模型误差估计与故障各分量的对应关系,辨识和隔离系统组件/执行机构故障;利用分散化滤波的结构,识别和隔离不同传感器故障。以卫星姿态估计系统为例,仿真验证该故障诊断方法,结果表明,分散化预测滤波与集中预测滤波相比,对多类型故障进行检测、识别以及系统重构的能力更强。
预测滤波;非线性滤波;故障诊断;卫星姿态估计系统
1 引 言
预测滤波是一种适用于具有未知输入或者模型误差的非线性系统的估计方法,它起源于Lu从系统控制的观点提出的非线性预测控制器[1-2]。该方法通过使系统输出与参考轨迹的误差方差和控制输入的平方和最小来获得控制输入。在此基础上,Crassidis将它发展成为具有随机测量过程的估计器[3-4]。这种估计方法对预测控制中的目标函数进行了修改,使得预测输出与测量输出的误差和模型误差的加权和最小,从而可以求出对应的模型误差估计,进一步可以修正状态估计。
由于预测滤波器是通过给出模型误差估计来实现状态估计的,因此它具有同时估计模型误差和系统状态的能力。将故障视为一种特殊的模型误差,则可以方便地实现对故障的诊断。针对预测滤波用于故障诊断的问题,目前已经有了一些初步的结果:文献[5]详细研究了预测滤波用于系统组件/执行机构故障诊断的方法,并提出使用低通滤波来提高对微小故障的检测能力;文献[6]在此基础上将该方法延伸到卫星姿态容错控制系统中,实现了对执行机构——飞轮故障的检测和系统重构;文献[7]指出预测滤波对系统组件/执行机构故障和传感器故障均能实现检测,并研究了使用渐进局部法来提高故障检测性能的方法;在此基础上文献[8]针对标准预测滤波进行故障诊断的问题,提出了将模型误差估计和输出估计误差两类残差相结合,实现对系统组件/执行机构故障和传感器故障进行检测、区分的策略。但是,到目前为止,使用预测滤波进行故障诊断的方法虽然能够区分系统组件/执行机构故障和传感器故障,对前者也能实现故障辨识,但是对于传感器故障却无法实现辨识,也不能实现对这种故障的隔离。
文献[9]推导了一种分散化的预测滤波结构,并初步验证了其对传感器故障进行检测和实现系统重构的能力。本文将在此基础上,使用分散化预测滤波对包括系统组件/执行机构故障和传感器故障在内的多类型故障进行检测和识别,实现系统重构,同时对其采用的方法和策略进行深入地研究。该方法利用预测滤波对模型误差的估计能力来实现对系统组件/执行机构故障的检测和识别;同时利用滤波器的分散化结构能够方便区分各个子系统故障的特点,实现对传感器故障的检测和识别。
2 分散化预测滤波算法
设非线性系统模型为
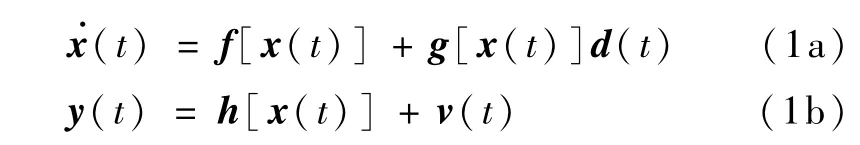
其中,x()∈Rn是状态向量,y()∈Rm是测量值,f()∈Rn→Rn、h()∈Rn→Rm是充分光滑的非线性函数,g()∈Rn×p是模型误差的分布矩阵,d(t)∈Rp是模型误差,v(t)∈Rm是测量噪声,服从均值为零、方差为R的高斯分布。
用标准预测滤波,即集中式算法进行估计的计算步骤为:由 t(k+1)时刻的测量 y(k+1)和 t(k)时刻的状态估计(k)可以按下式得到全局模型误差估计为
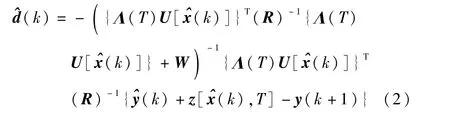
其中 T=t(k+1)-t(k)表示采样步长;然后可以根据系统方程(1a)和(1b)获得状态更新(k+1)和输出估计(k+1)[3]。
分散化预测滤波是借鉴联邦卡尔曼滤波的基本思想提出的一种改进标准预测滤波的算法。它的核心思想是将模型误差估计的计算分散到各个子滤波器中,然后由主滤波器对各个局部模型误差估计进行融合,以得到全局估计。
假定该系统可以分解为N个子系统,且这些子系统具有相同的状态方程和不同的测量方程
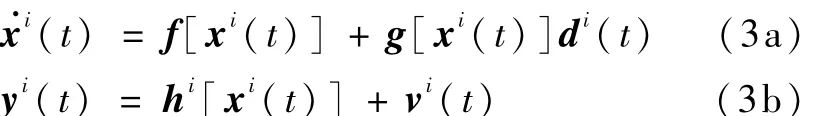
其中,上标 i(i=1,2,…,N)表示第 i个子系统,vi(t)是第i个子系统的测量噪声,为零均高斯白噪声,满足 E[vi(t)]=0,E{vi(t)[vi(t)]T}=Ri,E{vi(t)[vj(t)]T}=0,i≠ j,且有 h=[(h1)T…(hN)T]T,y=[(y1)T… (yN)T]T,v=[(v1)T…(vN)T]T。那么根据各子滤波器测量值 yi(k+1)可算出局部模型误差估计为
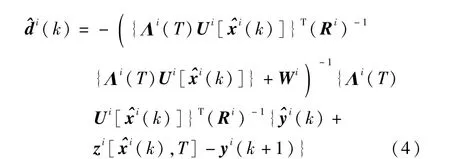
将标准滤波器的模型误差加权矩阵分配到分散化滤波的各子滤波器中,即,并且令
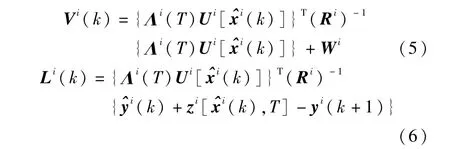
则各子滤波器的模型误差估计可以表示为
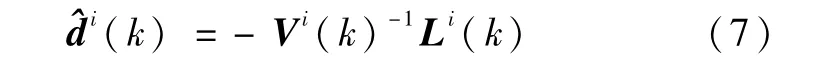
而全局滤波器的模型误差估计也可以改写为
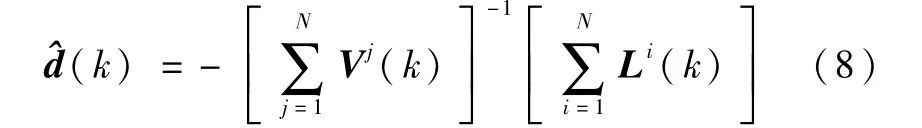
由此可以得到分散化预测滤波的核心融合公式
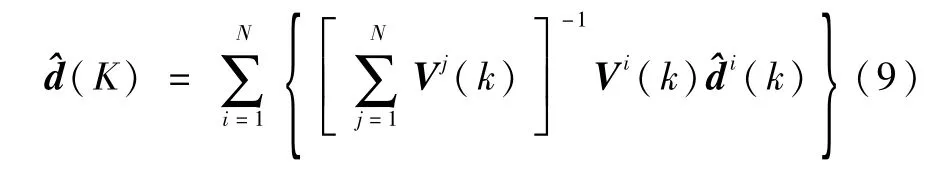
这里Vi(k)可以看作模型误差估计的信息矩阵,它的逆近似为模型误差估计的方差阵[8]。
3 基于分散化预测滤波的故障诊断方法
在进行分散化预测滤波故障诊断方法讨论之前,有必要首先介绍一下采用标准集中式预测滤波故障诊断的方法和性能。对于如式(1)表示的非线性系统可能存在两种类型的故障:系统组件/执行机构故障和传感器故障(所谓系统组件故障是指源自除执行机构和传感器外的其它部件且影响系统方程的故障,它与执行机构故障具有相同的形式)。用 δ(t)代替式(1)中的 d(t)来表示模型误差,那么系统组件/执行机构故障下的系统模型可以用式(10)表示
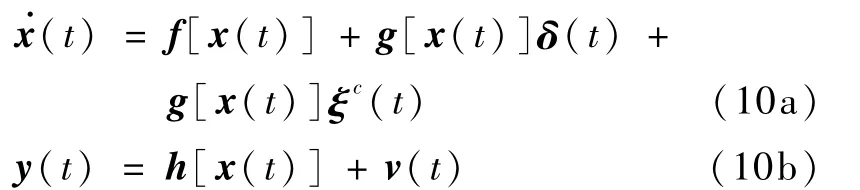
而传感器故障下的系统模型可以用式(11)表示
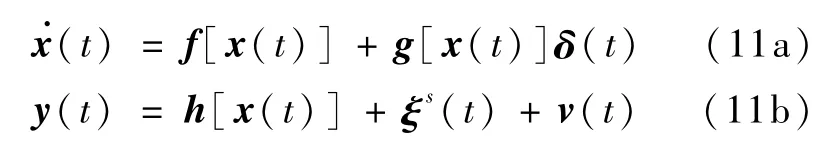
式(10)和式(11)中 ξc(t)和 ξs(t)分别表示系统组件/执行机构故障和传感器故障。本文只考虑这两种故障分别发生的情况。
基于滤波的故障诊断方法通常都是一种残差检验方法,预测滤波也不例外。用集中式预测滤波对如式(1)所示的非线性系统进行估计,并选择模型误差估计作为第一类残差,输出估计与测量之差(k)=y(k)-(k)作为第二类残差。取加权矩阵W=0,当系统组件/执行机构发生故障后,第一类残差和第二类残差分别为[8]
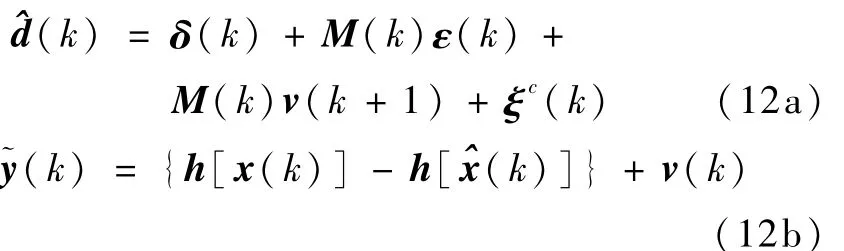
当系统发生传感器故障之后,第一类残差和第二类残差变为[8]
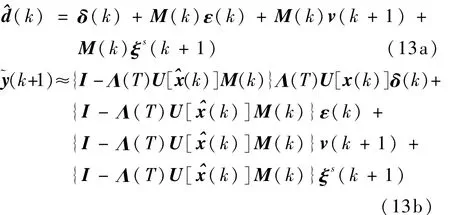
从式(12)和式(13)可以看到,预测滤波器给出的第一类残差无论是对系统组件/执行机构故障还是传感器故障均敏感(式(12a)和式(13a)中分别包含ξc和ξs),而第二类残差只对传感器故障敏感(式(12b)中不包含 ξc,而式(13a)中包含 ξs),因此,若系统组件/执行机构和传感器不同时发生故障,就可以通过将两类残差配合使用,并设置合理的检测门限的方法,实现对系统组件/执行机构故障和传感器故障的检测和区分。
从式(12a)还可以看出,对于系统组件/执行机构故障,残差各分量与故障各分量具有一一对应的关系,因此可以比较方便地实现系统重构,例如文献[8]所讨论的基于预测滤波的飞轮故障检测和重构方法;但是对于传感器故障,残差和故障并不具有一一对应的关系(见式(13a)和式(13b)),因此该方法不能具体指出故障源,当然也不能实现故障隔离和系统重构。为此,本文提出使用分散化预测滤波取代标准预测滤波的算法来实现故障的检测、辨识和系统的重构。
假定同一时间只有一种故障发生
1)如果存在某个子滤波器l,满足
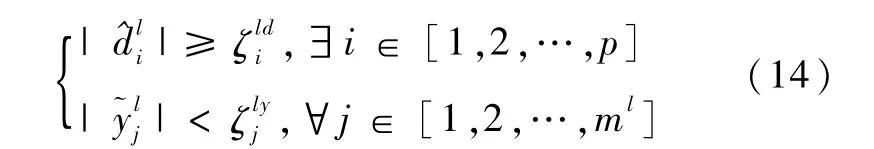
则判断是第i个系统组件/执行机构发生故障;2)如果存在某个子滤波器l,满足
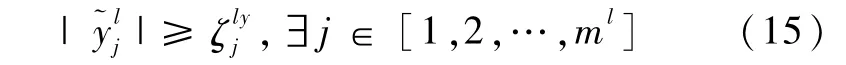
则判断是子滤波器l所对应的传感器发生故障;
3)如果对所有的子滤波器都有
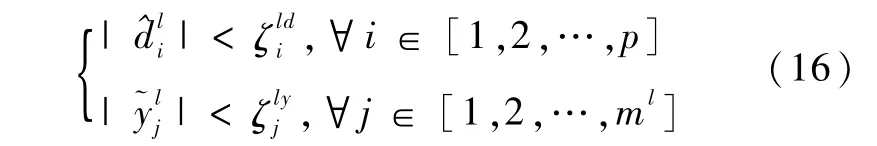
则认为没有发生故障。
进一步在故障检测的基础上可以很方便地实现系统的重构:对于系统组件/执行机构故障可以利用残差和故障的对应关系,重新配置未故障的组件或执行机构,使得系统组件/执行机构的输出相对故障前没有变化;对于传感器故障,则只需要将对应于故障传感器的子滤波器(假定是第l个子滤波器),从融合公式(9)中去掉即可,此时融合公式变为
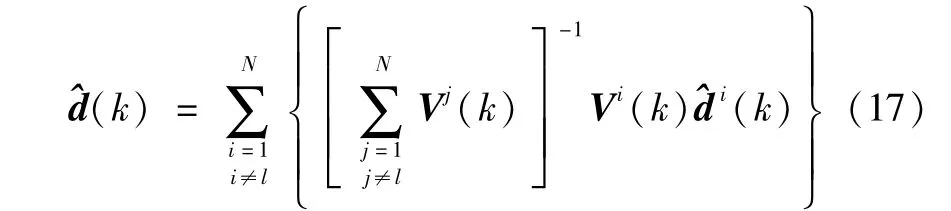
4 仿真实例
下面将通过1个三轴稳定卫星姿态估计系统,验证分散化预测滤波的故障诊断性能。卫星姿态估计所使用的传感器主要包括惯性测量单元、红外地球敏感器、太阳敏感器和GPS测姿系统。
惯性单元由6个正十二面体单侧安装的陀螺构成(见图1),安装矩阵为C
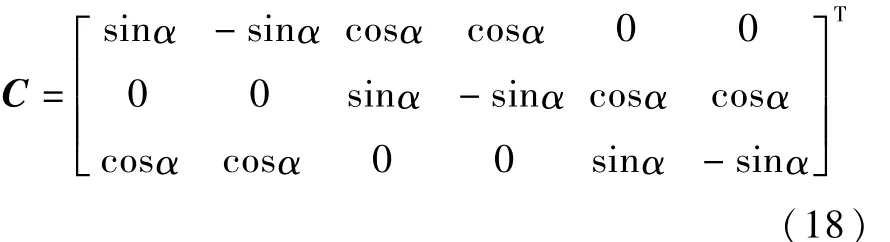
其中α=32.717 5°,单个陀螺的测量模型为
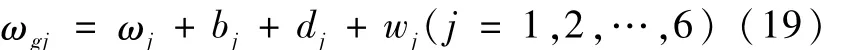
其中,ωj为真实的角速度在第 j个陀螺上的投影,ωgj为第j个陀螺的测量值,bj为相对测量轴的常值偏移,dj为测量误差与时间相关的漂移,wj为随机漂移的高斯白噪声,j=1,2,…,6。惯性单元的输出可以根据6个陀螺测量值由最小二乘法得出,即
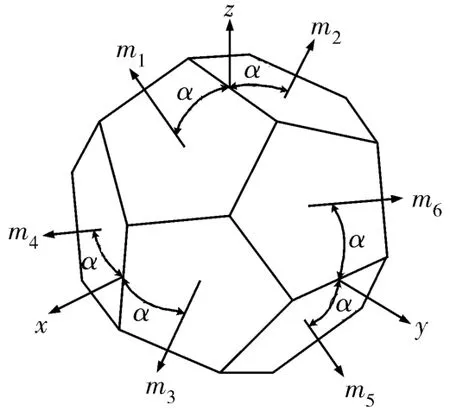
图1 正十二面体陀螺组件安装示意图
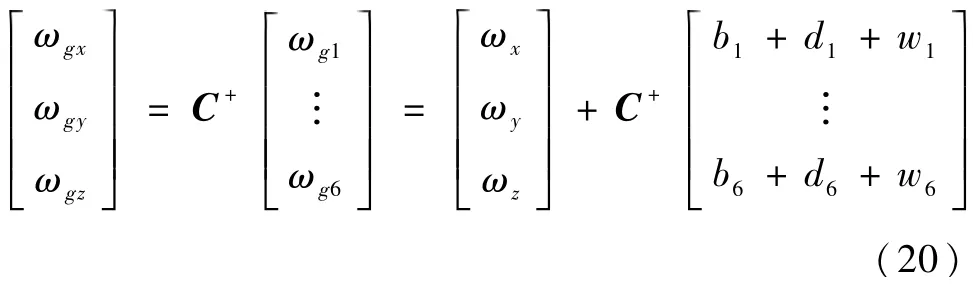
其中 C+=(CTC)-1CT。
用四元数姿态运动学方程和惯性测量组件模型构成滤波器的系统方程
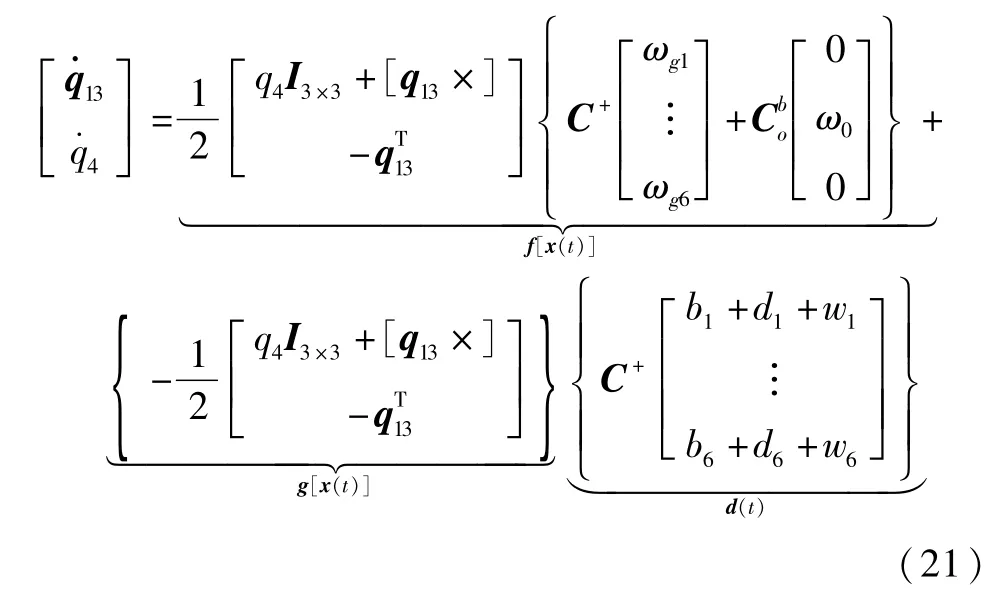
由地球敏感器[11]和太阳敏感器[11]构成的子滤波器1的测量方程为
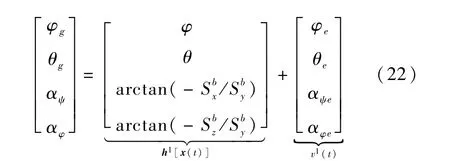
由GPS?测姿系统构成的子滤波器2的测量方程为
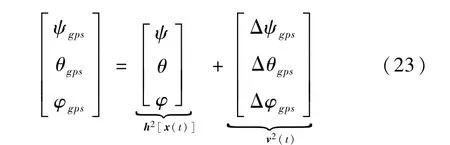
其中,测量误差 φe、θe、αψ、αφ、Δψgps、Δθgps和 Δφgps均假定为白噪声。对这样一个系统,采用式(14)-(16)所描述的检测策略对两个子滤波器的第一和第二类残差各分量进行检测。仿真中取门限ζ1di=0.08(°)/s(i=
(1)传感器故障的诊断和隔离
假设地球敏感器发生故障,其输出在200 s后出现了2°的偏差。根据式(15)可以判断出子滤波器1所对应的传感器发生故障。然后将故障传感器所对应的子滤波器从系统中隔离出去,只使用剩余的未故障的子滤波器进行滤波和融合。仿真曲线如图2所示。
从仿真曲线可以看到,对应于子滤波器1的两类残差的各分量都发生了跳变,并且多数都超过了检测门限,因此可以判断出子滤波器1所对应的传感器故障(见图2(a)和(b),点划线为检测门限)。子滤波器2没有感受到故障,其两类残差均没有变化(受篇幅限制略去了该子滤波器的残差曲线)。由于故障隔离后,传感器数目减少,因此全局滤波的精度有所下降,但不影响其正常工作(见图2(c))。
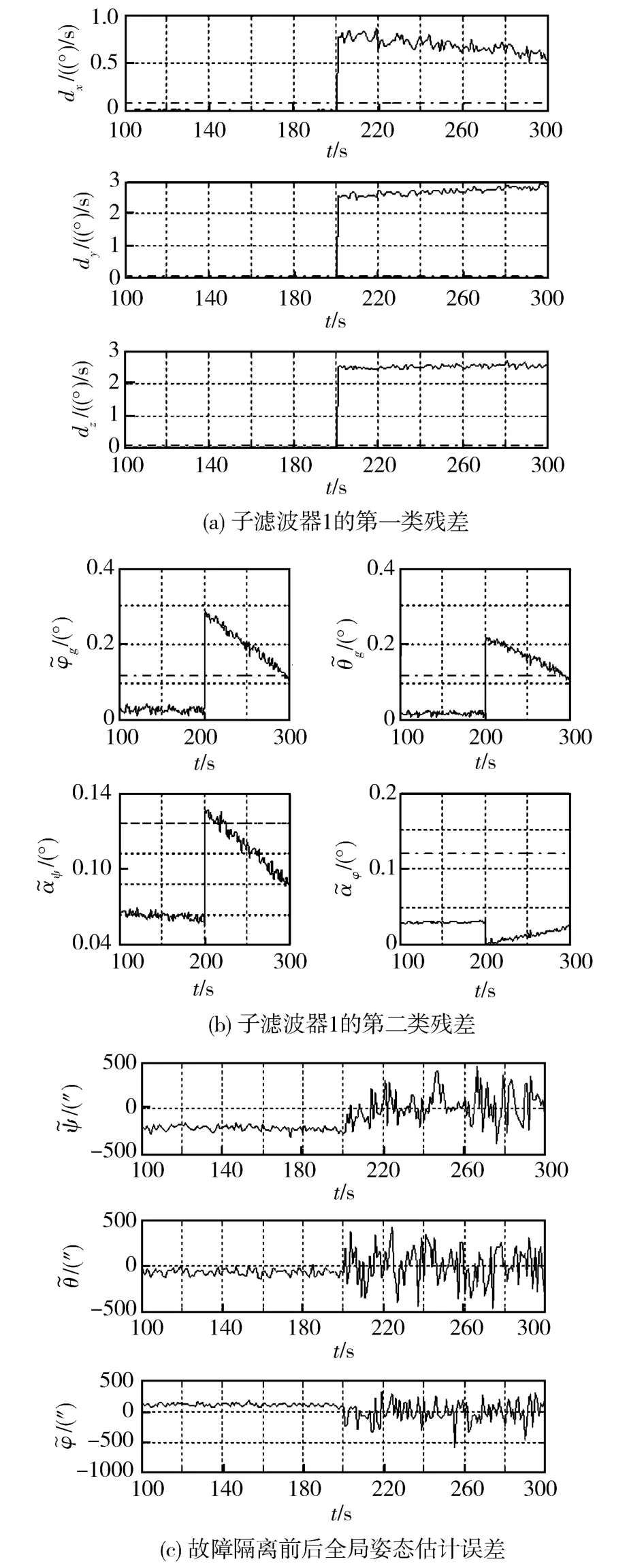
图2 分散化预测滤波对传感器故障诊断和隔离的仿真结果
(2)系统组件故障的诊断和隔离
假设惯性组件中第3个陀螺故障,其输出在200 s后出现了 0.5(°)/s的偏差,用式(14)可以判断出系统组件故障,也就是惯性组件故障。由于陀螺是六维的,而模型误差估计,即第一类残差是三维的,因此不能简单地依靠残差和组件的对应关系来判断具体的故障陀螺。由式(20)可以看到C+的第j列实际上就是在第j个陀螺输出数据的矢量方向。假定同一时间只有1个陀螺故障(编号为l),那么残差 ^d的方向应该与故障陀螺l的矢量方向,即C+l一致。因此,故障陀螺可以通过下式进行判断
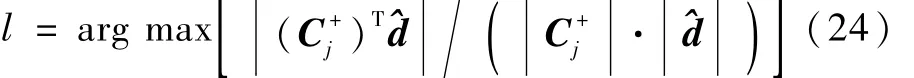
这里arg表示满足条件的j的编号。在故障陀螺被识别出来后将C中的第l行去掉,记为,其伪逆为
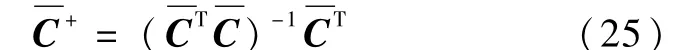
从仿真的结果来看,子滤波器1敏感到了该故障,其第一类残差发生了跳变(见图3(a)和(b),点划线为检测门限)。通过故障诊断策略检测以及式(24)所示方法识别出故障陀螺后,该故障陀螺被排除,系统被重构,残差重新恢复到0附近,全局滤波精度也没有发生明显的变化(见图3(c))。
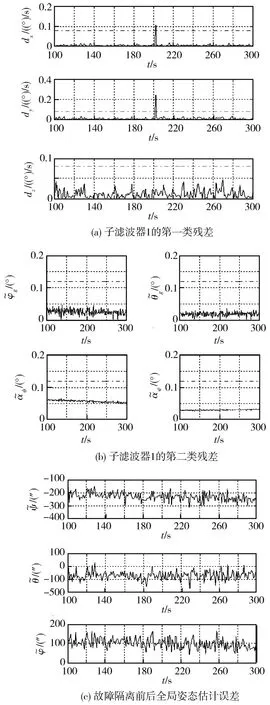
图3 采用分散化预测滤波对系统组件故障诊断和隔离的仿真结果
5 结 论
在使用标准的集中式预测滤波器进行故障诊断的时候,由于这种滤波器具有在状态估计的同时给出模型误差估计的能力,因此将系统组件/执行机构故障视为模型误差的一部分,可以实现对这种故障的诊断。而且,利用预测滤波的输出残差只对传感器故障敏感的特点,还可以实现对传感器故障的检测。但是,由于输出残差和传感器故障不具有一一对应的特点,因此,预测滤波器不能实现对传感器故障源的辨识。为此,本文在集中式预测滤波故障诊断的基础上,重点研究了采用分散化预测滤波进行故障诊断的方法。通过对每一个局部滤波器的模型误差估计和输出残差进行检测,并按照适当的检测逻辑,该方法能够与集中式预测滤波算法一样实现对系统组件/执行机构和传感器故障的检测;而且,由于每个局部滤波器分别对应特定的传感器,因此,分散化预测滤波还能够方便地实现对传感器故障的辨识,并在故障诊断的基础上实现系统的重构。本文以1个三轴稳定卫星姿态估计系统为例,仿真验证了使用分散化预测滤波进行故障诊断的方法,结果表明分散化预测滤波能够在进行状态估计的同时比较方便地实现对包括系统组件/执行机构故障和传感器故障在内的多种故障的检测和辨识,并完成系统的重构。
[1] Lu P.Nonlinear predictive controllers for continuous systems[J].Journal of Guidance, Control and Dynamics,1994,17(3):553-560
[2] Lu P.Optimal predictive control of continuous nonlinear systems[J].Int.J.Control,1995,62(3):633-649
[3] Crassidis J L,Markley F L.Predictive filtering for nonlinear systems[J].Journal of Guidance,Control and Dynamics,1997,20(3):566-572
[4] Crassidis J L,Mark ley F L.Predictive filtering for attitude estimation without rate sensors[J].Journal of Guidance,Control and Dynamics,1997,20(3):522-527
[5] Li J,Zhang H Y.Analysis of fault detection method based on predictive filters[J].Science in China(F),2005,48(3):335-353
[6] Li J,Zhang H Y.Controller reconfiguration against reaction wheel failure based on predictive filters[C].The 1stInternational Symposium on Systems and Control in Aerospace and Astronautics,Harbin,2006
[7] Li J,Chan C W,Zhang H Y.Asymptotic local approach in fault detection based on predictive filters[J].Journal of Guidance,Control and Dynamics,2005,28(6):1112-1122
[8] 李骥.非线性预测滤波理论及其在卫星姿态控制系统中的应用[D].北京航空航天大学博士学位论文,2006
[9] 李骥,张洪钺.预测滤波器的分散化结构[J].宇航学报,2005,26(增刊):23-29
Fault Diagnosis Method Based on a Decentralized Predictive Filter
LI Ji1,2
(1.Beijing Institute of Control Engineering,Beijing 100190,China;2.National Laboratory of Space Intelligent Control,Beijing 100190,China)
A new fault diagnosis method for a complex system with more than one type of faults is proposed in this paper.To distinguish different faults,two kinds of residuals generated from only one decentralized predictive filter are used,because they have different sensitivities to component/actuator faults and sensor faults.Even more,for a component or actuator fault,the source of it can be found exactly depending on the relationship between residuals and faults.And for a sensor fault,it can be detected and isolated easily by using the decentralized structure of predictive filters.To elaborate this method,a simulation for a satellite attitude determination system is presented.The simulation results demonstrate that the decentralized structure of predictive filters ismore powerful than the centralized one in fault diagnosis and system reconfiguration.
predictive filter;nonlinear filter;fault diagnosis and isolation;satellite attitude determination system

TP271.62,TP206.3
A
1674-1579(2008)03-0017-06
*863计划(2006AA704333).
2008-03-01
李骥(1978-),男,湖北武汉人,工程师,研究方向为航天器导航、制导和控制 (e-mail:jerem-lee@sohu.com)。

