巧妙联想 一题多解

王一吉

丰富多彩的联想，往往能沟通条件和结论，使解题思路变得更加清晰，也有助于良好思维品质的养成.在解题时，注意寻找题目的各种解法，一方面可以开拓思路，另一方面也可以克服对难题的畏怯心理.本文举例说明如下.

题目如图1，△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD.求证：BD=CD.

思考：对本题直接进行解答，一下子无从下手，似乎在条件与结论之间无法建立联系.如果我们根据问题所提供的条件∠CAD=30° 及AC=BC，进行联想，构造熟悉的图形，那么解法就会“油然而生”.

策略一要说明BD=CD，也就是要说明△BCD为等腰三角形.我们可以联想到构造底边上的中线、高或顶角的平分线.如果作出底边BC的高DF，则应有CF为BC的一半.又由∠CAD=30°，我们联想到直角三角形中30°角所对的直角边等于斜边的一半.因此，可以构造出一个直角三角形ACE，只需要说明边CE与CF相等即可.

证法1：如图2，过C作CE⊥AD于E，过D作DF⊥BC于F.

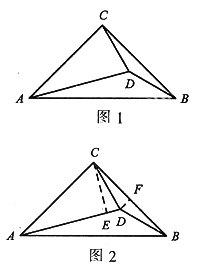
∵∠CAD=30°，

∴∠ACE=60°，且CE=1/2AC.

∵AC=AD，∠CAD=30°，

∴∠ACD=∠ADC=75°.

∴∠ECD=∠ACD-∠ACE=15°，∠FCD=90°-∠ACD=15°.

∴∠ECD=∠FCD.

∴△CED≌△CFD（AAS）.

∴CF=CE=1/2AC=1/2BC.

∴CF=BF.

∴Rt△CDF≌Rt△BDF（SAS）.BD=CD.

证法2：如图3，过D作DE⊥AC于E，过D作DF⊥BC于F.

∵∠CAD=30°，

∴∠ADE=60°，且DE=1/2AD.

∵∠ACB=90°，

∴DE∥BC.

∴∠EDC=∠FCD.

∴△CED≌△DFC（AAS）.

∴CF=DE.

∴CF=1/2AD=1/2BC.CF=BF.

∴Rt△CDF≌Rt△BDF（SAS）. BD=CD.

策略二由于△ABC是一个等腰直角三角形，我们可以联想到利用此三角形构造出一个正方形，从而可以得到等边三角形.

证法3：如图4，作△AEB，△AEB≌△ACB，则四边形AEBC为正方形.连接ED.

∵∠BAD=45°-∠CAD=45°-30°=15°，

∴∠EAD=∠EAB+∠BAD=45°+15°=60°.

又∵AD=AC=AE，

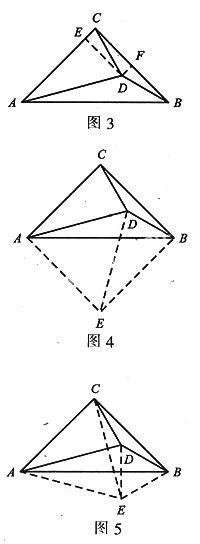
∴△ADE是等边三角形.

∴ED=AD=AC=EB.△EBD为等腰三角形.

∵∠DEB=90°-∠AED=30°，

∴△ACD≌△EBD（SAS）.

∴CD=BD.

策略三根据条件中的角度∠CAD=30°，∠CAB=45°，我们可以构造以AC为边的等边△ACE，如图5，从而可以得到图形中的△BDE是等边三角形，可得CD、DE、BE和BD都相等.

证法4：如图5，作△ACE，使△ACE为等边三角形，连接ED、EB.

∴∠CAE=60°，CE=AC.

∵AC=AD，∠CAD=30°，

∴∠ACD=75°，∠BCD=90°-∠ACD=15°.

∵∠ECD=∠ACD-∠ACE=75°-60°=15°，∴∠BCD=∠ECD.

又∵CD=CD，EC=AC=BC，

∴△ECD≌△BCD（SAS）.ED=BD.

∵∠CAE=60°，∠BAC=45°，∠CAD=30°，∴∠DAB=∠EAB=15°.

∵△ACE为等边三角形，AC=AD，∴AD=AE.

∴△ABD≌△ABE（SAS）.

∴BE=BD=DE，△BDE为等边三角形.

∴∠DBE=60°，∠DBA=30°，∠CBD=∠ABC-∠DBA=15°.∠CBD=∠BCD.

∴CD=BD.

总结：从以上各解法可以看出，尽管最后都是转化为证△BCD为等腰三角形，但利用题中条件计算出有关的角的大小很关键，比如△ACD中的各角，以及∠DAB、∠DCB等.计算出这些角后，就为后面的比较创造了有利条件.