全等三角形在生活中的应用

刘　顿

现实生活中，存在着许许多多、丰富多彩的三角形，也有不少全等三角形.学习了全等三角形的知识后，我们就可以利用它们来解决很多生活中的实际问题.现举例说明.

例1图1所示的是某房间木地板的一个图案，其中AB=BC=CD=DA，AE=EC=CF=FA.图案是由有花纹的全等三角形木块（阴影部分）与无花纹的全等三角形木块（中间部分）拼成.这个图案的面积是0.05 m2.若房间的面积是13 m2，那么最少需要有花纹的三角形木块和无花纹的三角形木块各多少块？

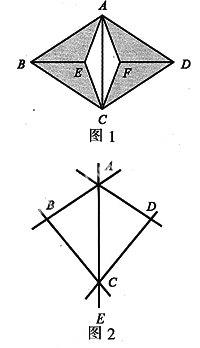
解析：因为一个图案由4块全等的有花纹三角形木块与2块全等的无花纹三角形木块拼成，且全等的三角形的面积相等，所以有花纹三角形木块的数目为（13÷0.05）×4=1 040；无花纹三角形木块的数目为（13÷0.05）×2=520.故最少需要有花纹的三角形木块1 040块，无花纹三角形木块520块.

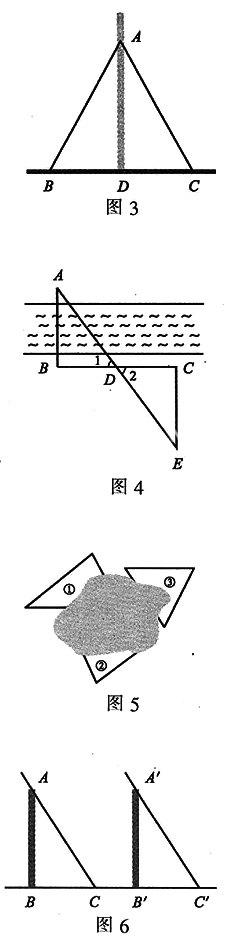
例2图2是一个简易的平分角仪器示意图，其中AB=AD，BC=DC.将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线AE，AE就是角的平分线.试说明理由.

解析：因为AB=AD，BC=DC，AC=AC，所以△ABC≌△ADC.所以∠BAC=∠DAC，所以AE是角平分线.

例3如图3，两根钢绳一端固定在地面铁桩上，另一端固定在电线杆上.已知两根钢绳的长度相等，则两个铁桩到电线杆底部的距离相等吗？为什么？请说明理由.

解析：相等.因为在Rt△ABD与Rt△ACD中，AB=AC，AD=AD，所以Rt△ABD≌Rt△ACD（HL），所以BD=CD.

例4如图4所示，要测量河宽AB，可先在岸上作AB的垂线段BC，并在BC上取点D，使BD=CD.然后再作出BC的垂线段CE，使A、D、E三点共线.这时量出线段CE的长就是所求的AB的长，为什么？

解析：因为AB⊥BC，CE⊥BC，所以∠B=∠C=90°.在△ABD和△ECD中，∠B=∠C，∠1=∠2（对顶角相等），BD=CD，所以△ABD≌△ECD（ASA）.所以AB=CE.

例5在一次知识大赛中，小颖同学分别画了三个三角形，不料都被墨迹污染了，如图5所示.她想分别画出与原来完全一样的三个三角形，是否可以做到？试说明理由.

解析：可以画出与三角形①、③相同的三角形.理由：在三角形①中保留了完整的两角和一边，可以根据“角边角”画出与①全等的三角形.在三角形③中保留了完整的两边和它们的夹角，故可以根据“边角边”画出与③全等的三角形.在三角形②中只保留了一个角，故不能画出与②全等的三角形.

例6如图6，太阳光线AC与A′C′是平行的，两根高度相同的木杆在太阳光照射下的影子一样长吗？为什么？

解析：一样长.理由：因为AC∥A′C′，所以∠C=∠C′.又因为AB=A′B′，∠ABC=∠A′B′C′=90°，所以Rt△ABC≌Rt△A′B′C′（AAS）.所以BC=B′C′.影子一样长.

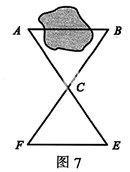
例7某铁路施工队在建设铁路的过程中需要打通一座小山修建隧道，设计时要测量隧道的长度.在山的前面恰好是一片空地.利用这样的有利地形，测量工人是否可以利用全等三角形的知识测量出隧道的长度？请你画出测量示意图，并说明理由.

解析：如图7，在山的两侧分别取A、B两点，在空地上取一点C，连接AC、BC，并延长，使AC=CE，BC=CF.连接EF，那么利用△ACB≌△ECF（SAS），有AB=EF，则E、F之间的距离就是A、B之间的距离，从而可以测量出隧道的长度了.