奥运数学趣题集锦

1. 体育老师在一次团体操队列选型设计中，先让全体队员排成一个方阵（即行与列的人数一样多的队列），人数正好够用。然后再进行各种队形变化，其中的一个造型分为5人一组，手执彩带变换图形。在讨论分组方案时，有人说现在的队员人数按“5人一组”将会多出3人，你说这可能吗？为什么？

2. 学校组织学生参观奥运场馆，原定上午8时发车。由于人员都到齐了，负责老师决定提前发车。发车时，学生小雨看手表发现时针和分针成90°的角（当时已经过了7时30分）。等到了目的地，小雨再一次看手表，时针在8和9之间，分针在时针后一格（表面一圈均匀分为60小格）。求实际出发时间和抵达时间，并计算路上共花了多少时间。

3. 在一个400米长的椭圆形跑道上，甲、乙两人同时同地起跑，已知甲比乙跑得快。甲第一次追上乙用了24分钟。超越后两人都提速，甲提速2千米/时，乙提速1千米/时。求第二次超越与第一次超越间隔多长时间？

4. 在绿茵场上，足球队员带球进攻，为什么总是尽力向球门AB冲？

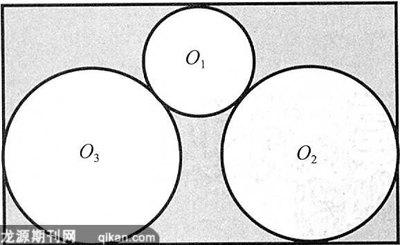
5. 某奥运场馆拟在一个矩形的草坪上布置三个圆形的花坛O₁、O₂、O₃（如右上图）。矩形草坪的长、宽分别为42m、18m。计划中花坛O₂和O₃的半径相等，它们的半径比O₁的半径大5m，且分别与矩形的两边以及O₁相切。求每个花坛的半径是多少？

6. 父子两人沿400米环形跑道同时同方向同地点出发跑步。两人速度保持不变。父亲未跑完一圈，儿子已跑完一圈。当儿子追上父亲后，转身向相反方向跑。当儿子再次与父亲迎面相遇时，恰在起点。问儿子一共跑了多少米？

7. 在奥运会的一场足球比赛中，甲队在距球门12米处获得一个任意球。已知足球运行的路线是一条抛物线，最高点距地面3.2米，且最高点距球门的水平距离为4米远。足球球门高2.43米（包括球门横梁），球门横梁直径为0.08米。

（1）如图所示，建立直角坐标系，求足球经过的抛物线的解析式。

（2）判断足球是否能射入球门（假设守门员未能扑到此球）。

8. 甲乙两人从家里同时出发去奥运场馆看奥运会，甲用一半时间以每小时a千米的速度行走，另一半时间以每小时b千米的速度行走；乙以每小时a千米的速度行走一半路程，另一半路程以每小时b千米的速度行走，若a≠b，则他们两人谁先到达目的地？

9. 一象棋比赛中每个选手都与其他选手赛一局，赢者得2分，输者得0分，和局各得1分。四同学在比赛结束后统计所有选手得分总数分别为1979、1980、1984、1985。已知其中只有一人统计正确。问选手共有几人？

1 0 . 某跳水运动员在进行10m跳台跳水训练时，身体（看成一点）在空中的运动路线是在如图所示的坐标系中经过原点O的一条抛物线（图中标出的数据为已知条件）。在跳某个规定动作时，正常情况下，该运动员在空中的最高处距水面32/3m，入水处距池边的距离为4m，同时，运动员在距水面高度为5m以前，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误。

（1）求这条抛物线的解析式；

（ 2 ） 在某次试跳中， 测得运动员在空中的运动路线是（1）中的抛物线，且运动员在空中调整好入水姿势时，距池边的水平距离为18/5m，问此次跳水会不会失误？说明理由。