弹库气体隔离系统数学模型研究

1 引 言

现代大型水面舰船为了满足作战能力的需要都装载有大量弹药,当弹药由于发生意外情况爆炸时，会产生大量的气体，导致舱内温度、压力迅速升高。为了减小这种高温、高压气体对弹药及弹库本身的危害，国外大型水面舰船通常在弹库顶部设置了泄压盖将高温高压气体排至大气,以降低弹库内部压力，同时启动快速喷淋系统进行降温处理[1]。

随着大量气体的排出以及喷淋系统的强降温作用，在排气的后期将导致弹库内部出现负压，此时外面的新鲜空气就会进入弹库。由于各种推进剂主要是由C、H、O、N等元素组成，因此爆炸产物中不可避免地含有H2、CO等易燃易爆气体组分[2]。燃烧爆炸后生成的易燃易爆气体与空气混合后，在空气中的体积浓度处于爆炸极限范围，有可能形成新的灾害，造成重大经济损失和人员伤亡。因此，为避免新鲜空气进入弹库，对弹库气体隔离系统展开研究是安全性设计上一个急需解决的问题。

2 爆炸混合气体流动特性

2.1 混合气体特性分析

为了对流场有一个真实的认识，必须掌握弹库爆炸后混合气体的流动特性。就流动方式而言，爆炸后混合气体与一般空气几乎没有区别，只是所含O2及H2、CO、CO2量有所不同，对气体物理特性并不造成重大影响，不足以改变流动的总方式。一般来说引起混合气体流动的因素是[3]：烟囱效应、温度变化引起的压差、外界风力和弹库内空调通风系统的影响。由于火灾时空调通风系统将及时关闭，因此无须考虑空调通风系统的影响。

2.2 烟囱效应

烟囱效应的特点是当舱室内外存在温度差时，在竖直方向存在一股上升气流，这种现象称为热压作用。它是由于温度差所形成的热压差造成的一股由底部到顶部的强大抽风作用所形成的气流。烟囱效应在舱室中的气压差特点如图1所示。

图1 气压差特点图

在舱室内外压力差为零处称为中和面，在中和面以下外界空气流入舱内，中和面以上舱内空气流向外界，中和面的位置由式(1)确定[4]：

(1)

式中:Ln为空气流入或流出量，kg/s；αn为流量系数，s2/m；An为对外开口面积，m2；ρ为舱室内空气密度，kg/m3；ρ∞为外界空气密度，kg/m3；hn为从水面起至计算层高度，m；h0为从水面起至中和面高度，m；sgn( )为符号函数。

2.3 热压的影响

在泄压盖前空气的流动可以近似地认为是不可压流体，考虑弹库温度发生变化时空气热胀冷缩对空气的影响，则当泄压盖打开时，在无气体隔离系统时，由于热压造成的泄压盖空气的自然流动，在外界没有风力影响下，其压差为：

Δp1=k1g(ρ-ρ∞)(h0-h)

(2)

式中,k1为空气的体胀系数，取k1=1.05。

2.4 外界风力

外界风向、风速对弹库内混合气体的流动有着显著的影响。风的压力和吸力会影响弹库内空气自然对流。风力作用于泄压盖表面的压力Δp如式(3)所示：

(3)

式中,cf为风压转换系数；ν为外界风速，m/s。

而外界风速一般是随着高度的增加而增加，根据参考文献[5]：

(4)

式中,ν10为距水面10 m处的风速，m/s；n为大气状态参数，n=0.2～0.25，沿海地区取n=0.25。

外界风速影响的最不利因素为风向垂直于泄压盖，此时的附加压差Δp2根据式(3)和式(4)确定为：

(5)

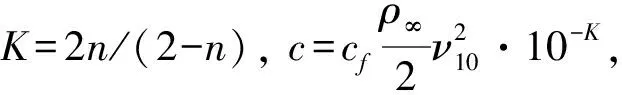
Δp2=c·hK

(6)

则总压差为：

Δp=Δp1+Δp2=k1g(ρ-ρ∞)(h0-h)+c·hK

(7)

根据流体力学原理，由压差引起的流动为：

(8)

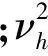
将式(7)代入式(8)中得：

(9)

现以喷头安装侧的泄压盖边为x轴，泄压盖垂直方向为y轴，泄压盖两边的交叉点为O点建立坐标系。由于排气弹库内爆炸混合气体水平流速较小，所以可以忽略它的影响，则在压差作用下通过泄压盖的流动近似为均匀等速流，即νh=νy，如图2所示。

图2 泄压盖设计流场图

根据流函数的定义，由压差引起的流函数为：

(10)

假设气体隔离系统的射流形式为缝式射流，且喷嘴喷出流体完全气化，则吹出的平面射流基本段的流函数为[6]：

(11)

式中，b0为喷嘴宽度，m；a为喷嘴紊流系数，一般取a=0.2；α为隔离系统向外倾斜的射流中心轴平面与泄压盖平面的夹角。

在此认为空气是不可压缩流体，所以可以将平面射流体看作势流，根据流场叠加原理，上述两股气流叠加后的流函数为：

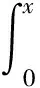
(12)

又因∂2ψ/∂x∂y=∂2ψ/∂y∂x，说明存在流函数ψ，设计流场为：x=0时y=0；x=H时y=0。

3 气体隔离系统数学模型

将边界条件代入流函数式(12)得：

当x=0、y=0时，流线为ψ0=0；

当x=H、y=0时，流线为：

(13)

根据流体力学可知，两条流线的流函数数值之差等于这两条流线间所通过的单宽流量[7]。此处即表示为在气体隔离系统运行时，通过泄压盖的空气量，即：

L=B(ψH-ψ0)=

(14)

式中H为泄压盖长度，B为泄压盖宽度，m。

式(14)中的前部分为无气体隔离系统在压差作用下通过泄压盖的空气量，即：

Lp=

(15)

令

(16)

气体隔离系统的流量为：

L0=B0b0ν0

(17)

式中,B0为喷嘴宽度，m。

将式(15)、(16)、(17)代入式(14)得：

(18)

因气体隔离系统要求阻挡外界空气进入弹库，所以要求L=0，故得：

(19)

根据式(16)、(18)可求得：

(20)

式(20)即为气体隔离系统满足安全设计要求的最终公式。

4 结 语

本文从理论上对气体隔离系统的隔离过程进行了分析，建立了气体隔离系统的数学模型，分析了气体隔离系统参数(初始速度、喷射倾角、喷射气流厚度)之间的关系，从理论上推导了气体隔离系统阻挡外界空气进入所需要满足的条件。如果再经过实验检验，得到进一步的验证，并以此为计算机仿真技术提供理论支撑，对弹库的安全性设计具有积极的作用。

[1] DARWIN R L,BOWMAN H L,HUNSTAD M, et al.Aircraft carrier flight and hangar deck fire protection history and current status[R]A671234，2005.

[2] 周起槐，任务正．火药物理化学性能[M]．北京：国防工业出版社，1983.

[3] 何嘉鹏,王东方,等. 防烟空气幕二维数学模型[J]．土木工程学报，2003,36(2):104-107.

[4] 日本防灾设施研究会．建筑防烟排烟设备[M]．安中义,译．北京：中国建筑工业出版社,1983.

[5] 孙一坚．工业通风[M]．北京：中国建筑工业出版，1985.

[6] 巴图林B B．工业通风原理[M]．刘永年,译．北京：中国工业出版社，1965.

[7] 王惠民.流体力学基础[M].北京：清华大学出版社，2005.