Matlab/Simulink仿真技术在舰船推进装置中的应用
景 民,陆金铭
(江苏科技大学 机械与动力工程学院,江苏 镇江212003)
推进装置的设计是舰船动力设计中最重要的环节,总体设计必须从船、机、桨的配合特性出发,合理地选配船、机、桨、传动设备的特性参数,实现船、机、传动设备、轴系、桨的最佳配合,保证船、机、桨在最佳状态下运行,即实现推进装置能量的最佳转换。因此,对舰船推进装置的模拟仿真也就是基于对这几大部分的建模,然后使用计算机技术进行仿真分析,根据仿真结果分析舰船动力推进装置的性能及控制规律[1]。
1 仿真实例
1.1 船机桨数学模型
1.1.1 船桨数学模型
船桨系统中包括推进装置的旋转运动和船的直线运动两个惯性体系(分别称为转动和平动系统)。这两个体系间有力(距)和能量的传递。力(距)和能量与这两个体系的共同工作状态有密切的关系[2]。
船舶在敞水中螺旋桨产生的推力Tp为:
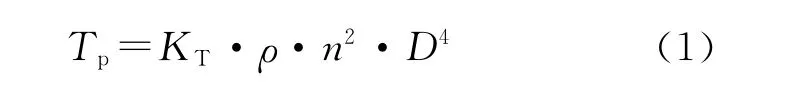
螺旋桨的负荷力矩(即螺旋桨上的水阻力距)Mp为:
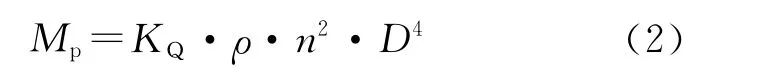
其中:KT——螺旋桨的推力系数;
KQ——转矩系数;
n——螺旋桨的转速;
ρ——水的密度;
D——螺旋桨的直径;
J——螺旋桨的进程比;
θ——螺旋桨的螺距角;
Vp——螺旋桨的进速。
通常情况下Kp、KQ与J和θ之间的关系无法用解析式表达,而需要利用螺旋桨的图谱获得。仿真时,可把KT-J,θ和KQ-J,θ曲线存入计算机,构成函数发生器。数字仿真情况下可以把曲线变成表格函数,断点数据存入内存,使用内插值法求值。为满足动态仿真的需要,要求使用的螺旋桨的特性曲线画在四个象限内。此特性曲线仅在较局限的工况范围才适合使用,例如当n→0时,J→∞。因此需要有其它的描述螺旋桨特性的方法,使之构成函数发生器,能够在大工况范围内使用。本文建立仿真模型时使用进角系数法,φ=arctg。式(1)和(2)可以写成:
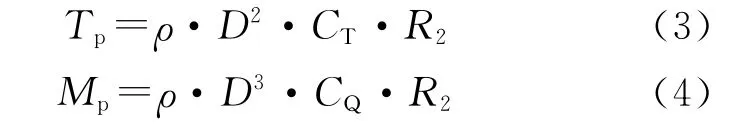
式中:CT=KTcos2φ CQ=KQcos2φ
对螺旋桨的四象特性(即CT-μ和CQ-μ特性)做Chebyshev多项式拟合,结果如下:
推力特性
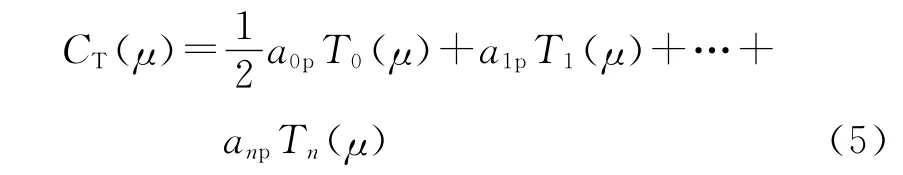
转矩特性
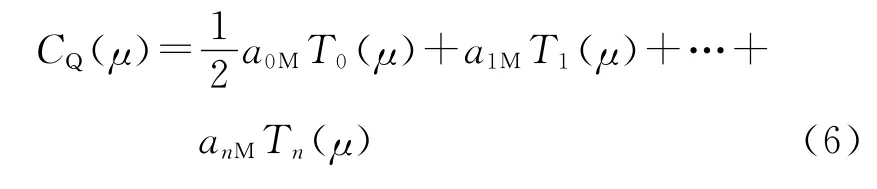
式中
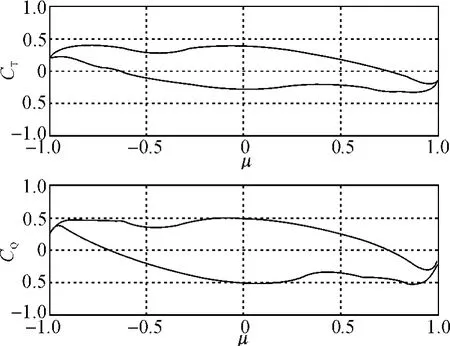
图1 CT-μ 和CQ-μ 特性曲线
在推进特性的实际仿真中,从精度和时间效率两方面考虑,决定采用8阶的Chebyshev多项式拟合[3]。通过 Matlab编程可以得到CT-μ和CQ-μ的特性曲线,所得到的曲线见图1。
由图1可以得到CT和CQ,在代入式(3)和(4),就可以得出推力Tp和转矩MP。
1.1.2 柴油机本体数学模型
柴油机的稳定工况是由给定负荷下曲轴的恒定转速来表征的,如果忽略机组的摩擦力矩,只有柴油机的输出转矩Md与转化至曲轴的阻力矩MC相等,即Md=MC。然而出现非稳定工况时,静平衡就会遭到破坏,使发动机曲轴的角速度发生变化,按动量矩原理可写成微分方程式为:
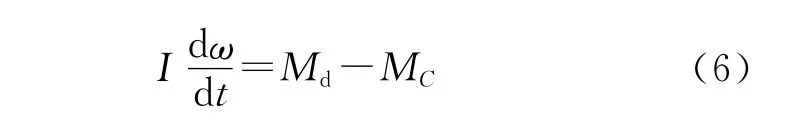
对于增压柴油机而言,有效转矩Md是循环供油量gc和有效效率ηe的函数,由于有效转矩ηe取决于两个主要参数:过量空气系数α和曲轴角速度ω,或是增压空气压力pK及ω;负载转矩MC是负载系数N和曲轴角速度ω的函数[4]。
通过泰勒级数变换和整理,可以得到柴油机的线性化模型:
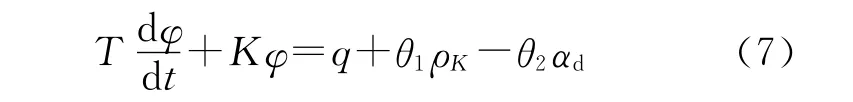
式中:T——发动机的时间常数;
K——发动机自平衡常数;
θ1——增压压力放大系数;
θ2——负荷调整放大系数。
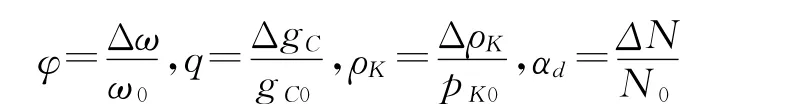
(ω0、gC0、pK0和 N0分别代表平衡工况下的曲轴角速度、每循环供油量、增压空气压力和负载系数)
1.2 船机桨仿真模型
1.2.1 船桨系统模型的建立
前面已经介绍了Kp和KQ,并说明它们是J和θ(螺距角)的函数。在这里通过对螺旋桨的设计图谱进行多项式拟合,从而构成Kp和KQ函数发生器,只要在“初始参数”模块中对应的输入螺距比、进程比、盘面比和桨叶数,就可以得到两个信号,信号1是KP的值,信号2是KQ的值。其中螺距比、进程比、盘面比和桨叶数可以通过图谱获得。
在螺旋桨给定的情况下,它的螺距比、盘面比和桨叶数可确定的值,但是进程比是螺旋桨的转速n、直径D和船的航速vs的函数 (J =)。在整个系统的仿真模型中,通过反馈系统就可以得到随航速和转速函数变化的进程比,使整个推进系统在大工况范围下进行仿真。图3所示为船桨系统仿真模型。
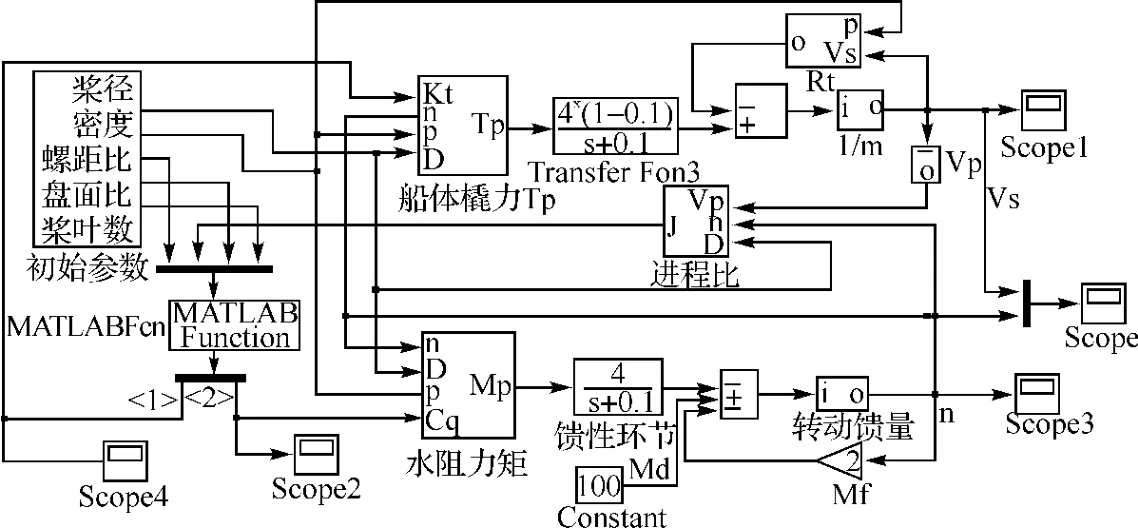
图2 船桨系统仿真模型
在图2所示的机桨系统仿真模型中,大多数的模块是由子系统构成的,这样系统的结构就有了层次。在建立模型时条理清晰,仿真运行时,也能及时发现错误,便于修改和调试。
1.2.2 柴油机本体仿真模型
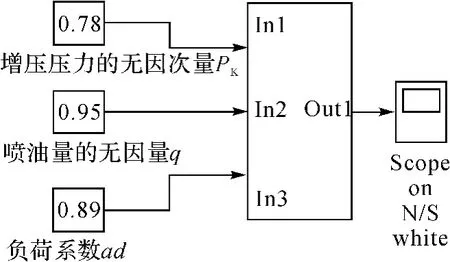
图3 柴油机本体仿真模型
为了便于阐述问题,只对柴油机本体进行建立仿真模型。依据前面所建立的数学模型,可以建立图3所示的仿真模型。把柴油机仿真模型的输出转换成转矩Md,并连接到船桨模型中,就构成了一套船舶推进系统的仿真。当然,本文所述的只是柴油机本体的仿真。
1.3 仿真结果和分析
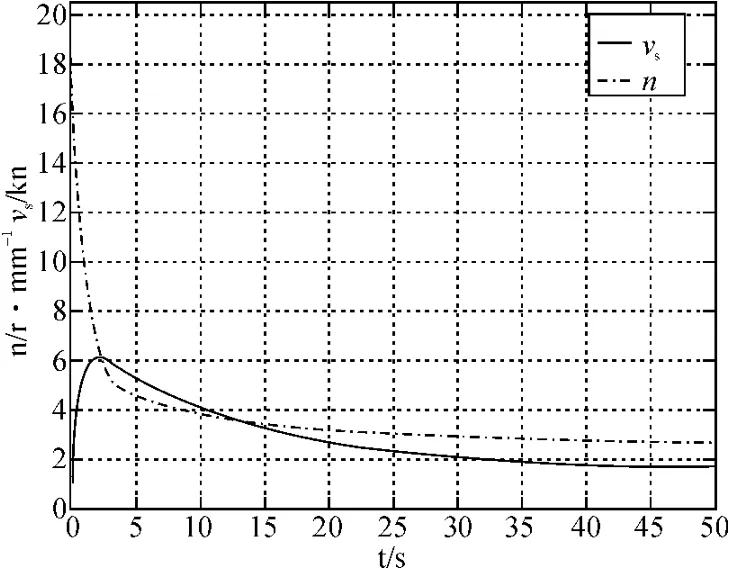
图4 螺旋桨转速n和船舶航速vs的仿真曲线
在前面建立的推进装置系统模型里,输入螺旋桨和柴油机的初始参数。确定系统的采样时间为50s。系统运行结束以后,就可以获得图4所示的螺旋桨转速n和船舶的航速vs仿真曲线。在模型的仿真过程中,由于J=,导致螺旋桨的转速不能从零开始,而是主机先给螺旋桨一定的转速,是船舶在系统的控制下开始航行,及航速从零开始增大。随时间的推移,大概在35s后,螺旋桨的转速和船舶的航速都趋于稳定。但是转速曲线在15s后就基本的趋于稳定,比航速曲线将近快了20s的时间。这与所输入的柴油机扭矩的变化状态有关,而且还与系统中各个环节的影响因素有关,例如船体总阻力RT,摩擦阻力矩Mf。
2 结论
通过对螺旋桨的设计图谱进行多项式拟合,使之构成函数发生器,从而使推进系统能够在大工况的情况下进行仿真,得出更合理、更准确的分析曲线。通过建立船桨运动模型,仿真模型不仅考虑了推进系统本身的特性,还考虑了船体阻力和摩擦力矩的影响。利用该装置可以实现舰舶在给定螺旋桨的各参数下对航速和螺旋桨转速进行仿真,各环节之间的仿真曲线相吻合,同时又与理论结果相吻合,证明了仿真模型的正确性和可行性,满足了仿真的要求。
[1]富 喜.模拟仿真技术在船舶推进装置中的应用[J].中外船舶科技,2004(3):16-20.
[2]翁史烈.船舶动力装置仿真技术[M].上海:上海交通大学出版社,1991.
[3]李殿璞,王宗义.螺旋桨特性四象限Chebyshev拟合式的建立与深水潜艇直航全工况运动仿真的实现[J].计算机仿真学报,2002(7):635-639.
[4]程国瑞.船舶动力装置原理[M].北京:国防工业出版社,2001.

