轿车集装箱运输设计方案的建模与仿真

李俊敏，唐伟敏，冯 飞

（武汉理工大学 交通学院，武汉430063）

中国轿车工业快速发展，越来越多的轿车运往境外。基于运输安全、运输成本和运输总量的综合考虑，通过水路采用集装箱运输是航运企业正在关注与探讨的新课题。

根据相关的航运公司前期的技术与经济调研表明，为使型号各异的集装箱运轿效益最佳，必须建立各型集装箱运轿图谱，为后续部分的技术设计提供重要依据。

1 建模原理与分析

集装箱运轿图谱设计，本质上是在限定尺寸内的空间物体装载优化问题。

1.1 数学模型

模型是由34个控制点所描述，根据所测得的控制点参数，可以得到轿车按如下方式放置的34个控制点的空间坐标。

通过对轿车模型在集装箱内进行适当的坐标平移和旋转后即可实现其在集装箱限定空间内的任何位置。

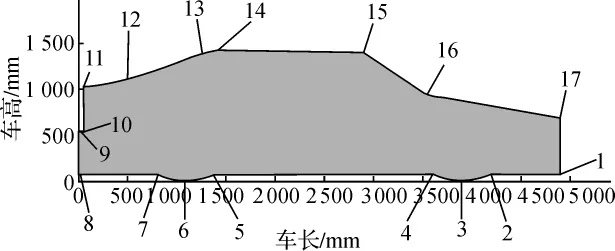
图1 家轿控制点模型（左右对称）

1.2 坐标变换原理

当两个空间直角坐标系（见图2）的坐标换算既有旋转又有平移时［1-2］，则存在3个平移参数和3个旋转参数，考虑到两个坐标系尺度不尽一致，从而存在一个尺度变化参数（m），共计有7个参数（即：3个位移坐标、3个旋转坐标、1个尺度参数）。相应的坐标变换公式为：

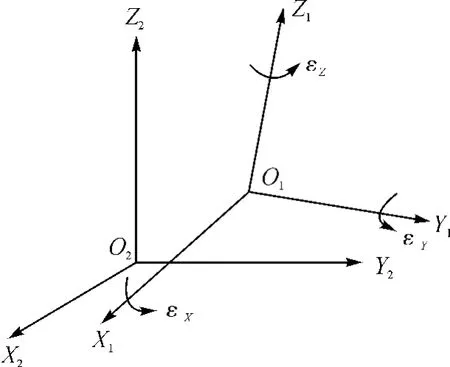
图2 两个空间直角坐标系

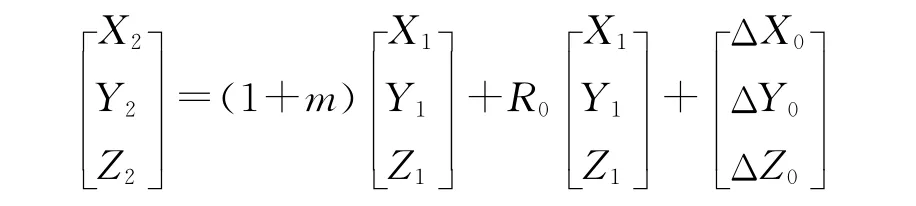
式中：εX，εY，εZ——三维空间直角坐标变换的3个欧拉角；

R0——空间旋转矩阵。

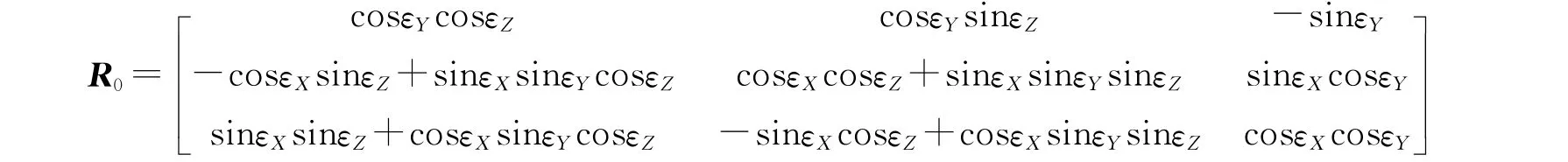
1.3 轿车间与箱轿间的干涉检测原理

1）轿车之间的干涉检测问题归结为空间的多边形与多边形是否相交的问题。当一个多边形的每个顶点都不在另一个多边形内部且反之也成立时，则两个多边形是不相交的。

采用奇偶法原理判断任意点（P）是否在多边形中。即以点P为端点，向左方作射线L。当L和多边形的交点数目C为奇数时，P在多边形内；为偶数时P在多边形外。

对几种特殊情况下的交点判别予以考虑，限于篇幅未详细论述。

2）家轿与集装箱之间的干涉检测就是将集装箱在三维空间的各方向缩小一定的空间，保证家轿都在集装箱内部即可。如果一个家轿的所有控制点都在集装箱内部，则此家轿肯定在集装箱内部，点在集装箱内部的判断与上述方法相同。

1.4 集装箱运轿的空间优化——人工智能判别

在数学变换的基础上，如果变换后的设定车辆数通过了干涉检测，则变换出的空间位置是可行的方案。在所有这样得到的可行方案中，如果某个可行方案几个关键距离的大小相对协调和充裕的话，就可以认为这个可行方案是最佳的。由于关键距离的协调性和充裕性由人工判断更为准确与合理，所以需要进一步结合人工智能的方法来判断［3］最佳布置方案。

2 集装箱运轿图谱的仿真

在上述数学建模的理论指导下，通过轿车控制参数的采集以及经过对多种方案的讨论和编程，在计算机上计算并仿真出几种轿车型在所选取典型的40HQ集装箱内的优化布置形式和相关控制参数，分别表述如下。

2.1 典型轿车的运输图谱

1）中级型及以上轿车（4辆）；

2）经济型轿车——富康（5辆）。

（注：中型轿车以标致307车型为代表；大型轿车以天籁车型为代表。）

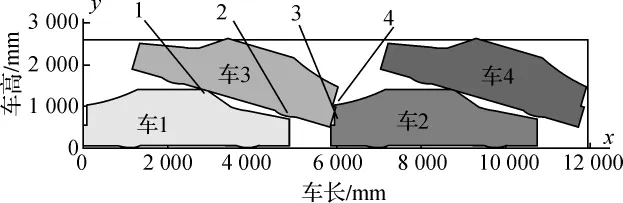
图3 天籁布置示意图

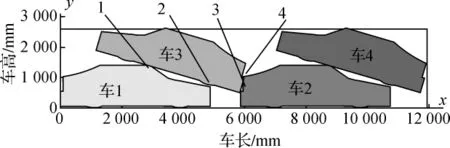
图4 标致307布置示意图

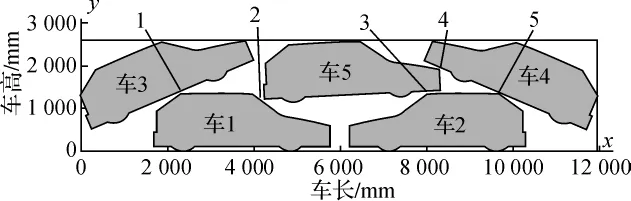
图5 富康布置示意图

2.2 各型轿车的各车间检测数据汇集

通过编程计算可以精确得到各车的三维坐标值与各家轿间的干涉检测数据，部分关键数据见表1～3。

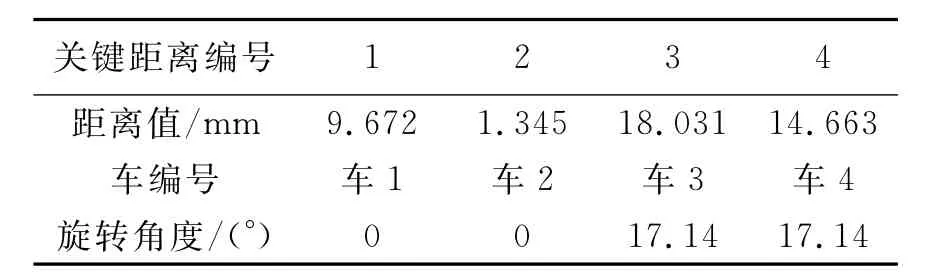
表1 天籁各车之间关键的关联距离值和旋转角度

表2 标致307各车之间关键的关联距离值和旋转角度

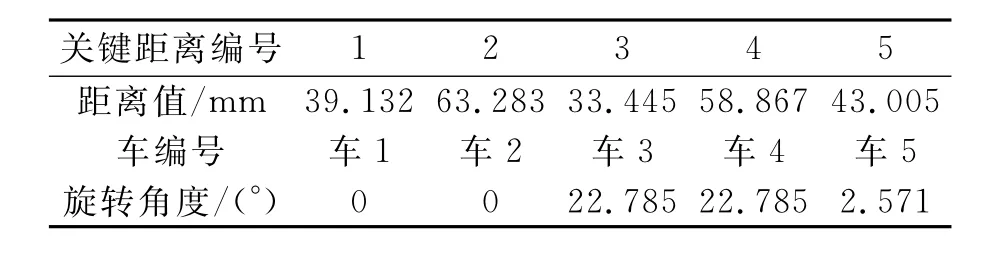
表3 富康各车之间关键的关联距离值和旋转角度

表格中的旋转角度指家轿在集装箱长度和高度方向的转角；天籁各车之间关键的关联距离值太小，可以通过控制点参数的处理予以解决。

3 结束语

1）通过建立家轿在集装箱内布置的数学模型与计算，可以快捷、精确地实现多种型号集装箱运输各型家轿的空间优化布置方案。

2）针对东风系列的家轿车型，实现了在所选典型40HQ集装箱内各种家轿车型的优化布置仿真方案。

3）通过数学建模与仿真为后续运轿支架的技术设计奠定的基础。

［1］梅家斌，欧贵兵.线性代数——应用与模型［M］.长沙：湖南大学出版社，2001.

［2］刘丁酉.矩阵分析［M］.武汉：武汉大学出版社，2003.

［3］［美］Thomas Dean.Janes Allen.人工智能——理论与实践［M］.顾国昌，刘海波，译.北京：电子工业出版社，2004.