深圳西部水域船舶流分析

汪益兵，庄 元

（1.国际海运职业技术学院 航海工程学院，浙江 舟山316021；2.武汉理工大学 航运学院，武汉430063）

深圳西部水域是进出各港区码头、抛锚待泊的唯一通道，也是大量往返珠江三角洲与香港、澳门之间的船舶必经之地。国家经济的快速增长和粤港跨境联系的不断增加，带来了对水运的大量需求。目前进出深圳西部水域的班轮航线密集，船舶日益增多，水上交通更加繁忙与复杂。仅船舶流量而言，1996年深圳西部水域的年船舶流量约为11万艘次，而2005年则高达40万余艘次。了解和掌握这一区域交通流的基本变化规律，对海事机构科学合理地实施船舶交通管理有着重要的意义。

1 船舶流分布

深圳港西部从龙鼓水道到警戒区、妈湾航道一带都是船舶密集区。该区域的船舶流量大，其中以300总吨以下的小型船舶约占绝大多数，由于大铲锚地验关的影响，南下船舶经常形成船舶群。警戒区附近的进口船舶，蛇口港区、赤湾港区、妈湾港区的出口船舶在此交汇，交通态势比较复杂。

1.1 数据来源

分析所采用的数据来源见表1。

表1 船舶流分析数据来源

1.2 船舶流组成

根据深圳海事局提供的船舶流量资料，对船舶交通流量按船舶种类和船舶尺度进行了统计分析［1-2］，见图1-4。

1.2.1 不同种类船舶日交通比例

图1 铜鼓岛断面观测数据

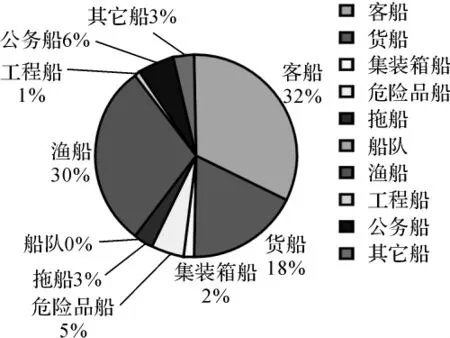
图2 铜鼓岛至内伶仃观测断面观测数据

1.2.2 不同尺度船舶日交通比例

图3 铜鼓岛断面观测数据

图4 铜鼓岛至内伶仃观测断面观测数据

1.3 船舶流时间分布

同时根据深圳海事局提供的船舶流量资料，对船舶交通流量按不同时间段进行统计分析，见图5、6。

1.3.1 月分布

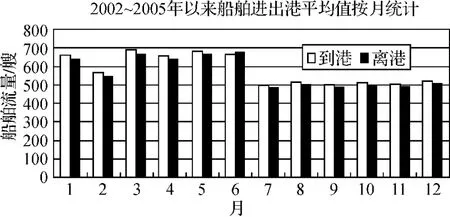
图5 船舶流月分布

1.3.2 日分布

图6 船舶流日分布

2 船舶流分析

1）西部辖区船舶交通流逐年增加。2004年进出深圳西部港口的船舶约19万艘次，另从珠江口航经深圳西部水域进出香港的船舶近17万艘次。该水域的船舶年交通流量近36万艘次，日均交通流量超过1 000艘次。2005年进出深圳的船舶为25.9万艘次，其中到达西部港的船舶就高达23万艘次。

2）日均统计表明，从7∶00时～17∶00时区域船舶流运行强度较大。

3）西部港区船舶交通流密集。通航船舶流总量的82.4%以上从西部港区水域通过，其中主要船舶为集装箱船、货船、客船，它们分别占30.4%，24.1%，19.5%，渔 船 的 比 例 高 达11.64%。从船舶长度上小型船舶占了绝大多数，长度为50m以下的船舶比例达到了89.1%，而长度100m以上的船舶不足5%。

VTS报告表明300t以上船舶活动较频繁的地区为妈湾港区（0～3泊位），进出赤湾港区，蛇口港区二突堤南集部码头及SCT码头附近。

4）西部VTS报告区域船舶流（非高速船）平均速度为7.72kn，与已有的国外港区通航安全速度相近。

3 船舶流预测

3.1 预测方法

传统的预测方法主要有灰色系统、指数平滑法以及神经网络等。考虑到现有交通流量数据少、数据收集难度大、流量变化规律不明显等特点，在预测未来一定年限到离港船舶交通流量时，采用了最新发展的支持向量机方法。

3.2 基本原理

给定l个训练样本（x1，y1），（x2，y2），…（x1，y1），xi∈X⊆Rn，yi∈Y⊆R，i＝1，2，…，l。

假设通过结构风险最小化，支持向量机可以获得回归函数：

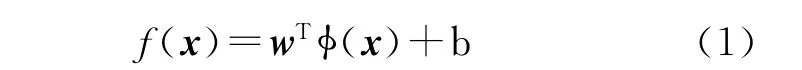
式中：w——权系数向量；

φ（x）——输入空间到高维特征空间的非线性映射函数；

b——偏置。

参数w和b可以通过最小化如下的规则风险函数得到：

式中：C——惩罚因子。

为了估计w和b，通过引入松弛因子ξi（＊）

（ξi（＊）≥0），式（2）可以写为：

最小化）

受限于yi＝wTφ（xi）-b≤ε+ξi

为了求解式（1）、（2）线性不等式约束条件下的二次规划问题，采用拉格朗日乘子法，通过求解如下的对偶函数：

最大化w（α（＊）i）＝

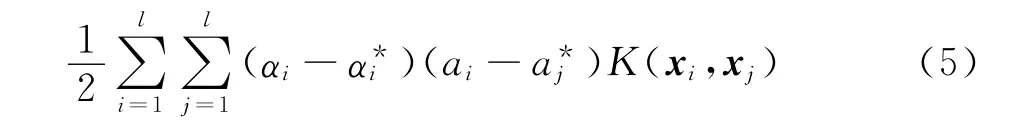
受限于

式中：α＊i——拉格朗日乘子；

φ（xj））＞K（xi，xj）；

K（xi，xj）——核函数，K（xi，xj）＝（φ（xi），φ（xj））。

这样，回归函数可以写为：

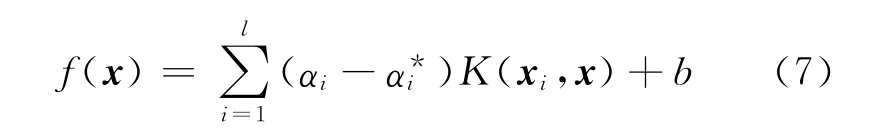
3.2 预测结果与分析

采用1996～2005年深圳港到离船舶量为样本数据，模型预测结果与实际值见图7。

图7 模型预测结果与实际值比较图

从总体看，预测结果与实际值拟和良好（趋势拟和良好，重峰值点捕捉准确）。预测结果值比实际值略微偏小，表明模型有一定的可信度。

运用该模型进一步预测2010年与2015年到离深圳港的船舶流量预测结果分别为：48.5万艘次和81.7万艘次。

4 结束语

通过对深圳西部水域的船舶流量现状分析以及预测可以看出，辖区的船舶日益增多。随着铜鼓航道的开挖和使用以及大铲湾集装箱码头的建设投产，未来船舶流量的发展势头可能甚至比预测来得更猛。对此海事机构应做好充分的应对措施，以缓解日益增加的船舶流带来的通航压力。

［1］吴兆麟.海上交通工程［M］.大连：大连海事大学出版社，1993.

［2］邱 民.船舶交通工程学［M］.北京：人民交通出版社，1991.