基于模糊C均值聚类的柴油机故障诊断

王志华，赵 冬，余永华

（1.武汉理工大学 能源与动力工程学院，武汉430063；2.青岛海事局，山东 青岛266011）

目前内燃机的故障诊断主要是利用信号分析处理技术提取表征内燃机状态的特征参数，通过特征参数判断内燃机的状态，并进一步判断是否存在故障及故障种类。研究表明［1-2］，一个有故障的被测系统，其测试数据中必然包含各种复杂的模糊化联系。常规逻辑推理方法无法从大量的测试数据中既快又准地诊断出故障部位。因此提出在被测系统正常运行的情况下，可先测得一批数据，由于系统功能本身所决定，这批样本点必有内部的联系；采用模糊聚类分析的方法，对样本点进行分析，得出正常系统的标准功能模式；再对系统实际运行时的测试值进行模糊聚类分析，一旦系统出现故障时，其聚类中心必定与原先正常时的标准模式发生偏移。根据模糊距离的分析和计算，可以得出哪些系统功能以多大的隶属度发生了故障。显然，这种与标准模式相比较的方法，可以说是一种模式识别的方法。

1 模糊C均值聚类算法

模糊C均值聚类算法中，C是指将有限样本集X＝｛x1，x2，…，xn｝划分成C 类，各样本以一定的程度隶属于C个不同空域。用μij表示第j个样本隶属于第Ⅰ个类的隶属度，μij满足如下条件：

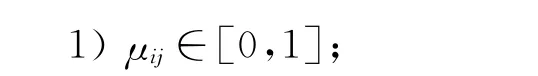
2）＝1，∀i，即每个样本对全部聚类中心隶属度之和为1；

3）∈ （0，1），∀i，即每个聚类中心包含的样本个数介于0和n之间。

模糊C均值算法的出发点是基于对目标函数的优化，通过对平方误差函数求最优值：

式中：U——初始隶属度矩阵；

m——权重指数，m∈［1，+∞］；

V——聚类；

V＝（V1，V2，…，Vi，…，VC）T；

dij——样本到中心矢量的距离，

dij＝‖Sj-Vi‖；

Sj——第j个样本；

Vi——第i个聚类中心矢量。

可以看出，模糊C均值聚类算法的实质就是寻找这样一组中心矢量，使各样本到其的加权距离平方和达到最小。

通过对目标函数的优化，便可以找到μij和dij的关系。利用拉格朗日乘子法使E（U，V）取极小值，最终可以得到：

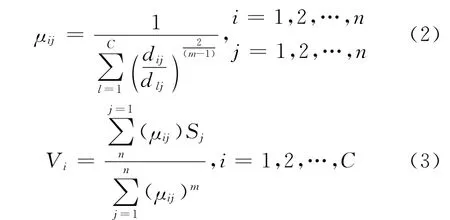
据此，若样本集X、聚类类别数C和权重系数m为已知，就能通过迭代算法确定最佳模糊分类矩阵和聚类中心。

2 模糊C均值聚类算法的一般步骤

根据上述模糊C均值聚类算法的原理，其计算步骤如下［3-5］：

2.1 确定C值，即对样本进行初步分类

初始矩阵的确定可采用模糊传递闭包法先对样本进行组合，得到初始隶属矩阵。该方法的作用对象是样本矩阵Sij（i表示样本序号，j表示样本的某一特性），算法如下：

1）样本矩阵初始化。可采用极值标准化公式把数据压缩到［0，1］。

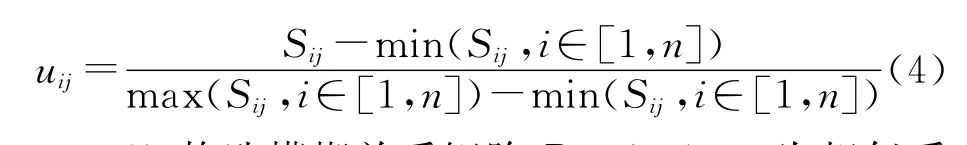
2）构造模糊关系矩阵R＝（rij），rij为相似系数，即描述样本i和j之间的相似程度。采用最大-最小法求解。

3）求出模糊等价关系矩阵R～。通过平方计算法可以快速求得R～，即依次求出R2，R4，…，R2k，直到R2k＝R2k-1为止，这时R～＝R2k。

4）采用λ-截矩阵法进行分类，λ∈［0，1］是R～中的隶属度，按不同的隶属度对模糊等价关系矩阵R～作λ-截矩阵后，所得的Rλ也具有等价关系，并给出了一个λ水平的分类，从而把样本分成不同的C类。

2.2 进行精确聚类分析

1）直接用样本均值，计算各类样本的初始聚类中心V（0）1，V（0）2，…，V（10）C。

2）求各样本与这几类样本中心的近似程度。采用最大-最小法。

式中：uik——样本初始化矩阵的元素；

vjk——样本中心的元素；

rij——第i个样本与第j个样本之间的近似程度。

3）计算初始隶属矩阵U（0）。

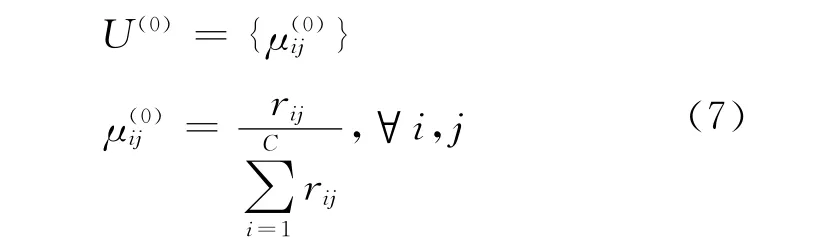
4）给定m，计算U（l）和V（l）i（l为迭代次数）。

5）给定任意小正数ε，检验是否满足

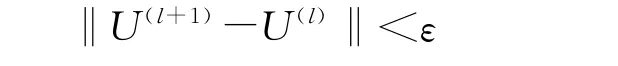
若满足条件则迭代结束；否则，回到2.2中的2）继续迭代，最终得到分类矩阵U和聚类中心V。

3 诊断原理

模糊聚类分析的过程，是一个把多个特征参数的冗余或互补信息依据某种准则进行信息融合，从而获得标准特征模式的过程。

模糊模式识别问题可描述为：已知C个已知模式A1，A2，…，AC和一个待检模式B，都是论域U上的模糊向量，试问待检模式B与哪个已知模式最接近。

当已知模式与待检模式都用模糊向量表示时，模糊模式识别问题就简化为两个向量的比较和择近问题，也就是比较待检模糊向量B与各已知模糊向量AC之间的贴近度。设每个模式A都是论域U＝｛u1，u2，…，uM｝中的一个模糊向量，若有j∈（1，2，…，C），使σ（B，Aj）＝） （9）则称B与Aj最贴近，也就是待检模式B应归入已知模式Aj中，从而完成故障识别。

式（9）中的σ称为两个模糊向量的贴近度。模糊贴近度可以是相似系数或者距离，

4 诊断实例

选取在不同状态下柴油机表面振动信号的时域、频域、时频分析的特征参数组成特征向量用于模糊模式识别。表1列出了柴油机再五种不同状态下的部分特征向量。应用模糊C-均值聚类算法，对以上10个样本向量利用最大最小法求出模糊贴近度并构造模糊关系矩阵R，求出模糊等价关系矩阵R～，进行λ-截矩阵分类，并根据机理将其大致分为5类。

在利用均值法计算初始聚类中心V（0）I（I＝1，2，…，C），并计算U（0），取m＝2，ε＝1×10-5，通过式计算U（I）和V（I）i，并反复迭代进行精确聚类分析，最终得到分类矩阵U和聚类中心V。

利用模糊C均值聚类很好地将向量1和向量2，向量3和向量4，向量5和向量6，向量7和向量8，向量9和向量10分别聚类。这一点可以从分类矩阵的数值中得出结论。如果有新的样本向量需要识别，只需计算它与聚类中心的几种模式的模糊贴近度即可。

表1 柴油机在五种不同状态下的部分特征向量

5 结论

1）柴油机表面振动信号的时域、频域、时频分析的特征参数组成特征向量可表征柴油机的状态；

2）运用模糊C均值聚类方法可以准确地对表征柴油机状态的特征向量进行分类识别。

［1］王志华.基于模式识别的柴油机故障诊断技术研究［D］，武汉：武汉理工大学，2004.

［2］张邦礼，尹朝东，曹龙汉.柴油机故障诊断中的遗传与模糊C-均值混合聚类分析算法［J］，计算机工程与应用，2002（3）：254-256.

［3］Erigui II，Krishnaparam R.Clustering by Competitive Agglomeration［J］.Pattern Recognition，1997，30（7）：1109-1119.

［4］Pal N R，Bezdek J C.On Cluster Validity for the Fuzzy c-Means Model［J］.IEEE Trans.Fuzzy Systems，1995，3（3）：370-379.

［5］高新波，李 洁.模糊C-均值聚类算法中参数m的优选［J］.模式识别与人工智能，2000（3）：8-9.