纵向规则波中参数横摇的数值模拟

付丽坤，蒋志鹏

（上海交通大学 船舶海洋与建筑工程学院，上海200030）

参数横摇是阻尼较小的船在顶浪和接近顶浪的情况下，遭遇一定频率的波浪时，伴随着显著的纵摇、升沉运动，船舶将在短时间内产生很大横摇角的现象［1］。发生参数横摇的条件包括：横摇周期约为波浪周期的两倍，波长近似船长，波高超过定值，横摇阻尼较低。

参数横摇的研究工作在20世纪30年代已经开始，当时人们主要基于简化的数学模型对方程进行解析解研究，目的仅限于定性分析［2］。1998年10月集装箱船APL CHINA号发生参数横摇事故后，研究重点转向了设计阶段对参数横摇的实际预报，以避免运行中船舶倾覆的危险。

1 参数横摇研究的几种经典模型

在顶浪或随浪中，当波峰、波谷经过全船时，船体周围的压力不断变化，这种压力差引起垂荡，结果不再是常数，而是变化的。取正弦波的简单情况，在顶浪情况下方程为：

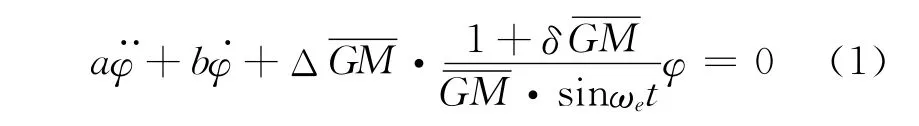
式中：φ——船舶横摇角位移；

a——横摇的虚质量惯性矩系数；

b——阻尼力矩系数。

上述马休（Mathieu）方程［3］是研究参数横摇的基础，虽然不同的学者采用了不同的数学模型，但是基本的理论都来源于Mathieu方程。马休方程的特点是：在无阻尼情况下，当频率为某些值时，解趋近于无穷大。这些频率所对应的周期值为：是船的固有周期。

基于经典的马休方程理论，目前已有多种参数横摇的数学模型，均可有效模拟参数横摇幅值。

Alberto Francescutto、Gabriele Bulian 和Claudio Lugni［4-6］提出了一种简洁的数学模型——1.5自由度的横摇方程：

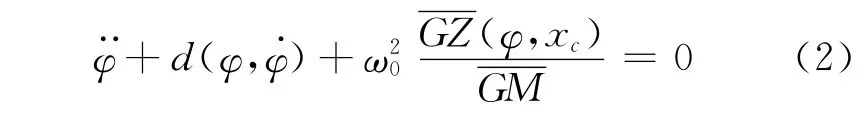
式中：d（φ）——阻尼方程；

ω0——静水中的横摇固有周期；

（φ，xc）——波浪中的复原力臂。

对于确定的简谐波，可以采用船模试验和静水力计算的方法确定横摇方程中的未知项。

Marcelo A.S.NEVES、Nelson A.PéREZ［7］等人提出了升沉-横摇-纵摇三种运动完全耦合的参数横摇模型：

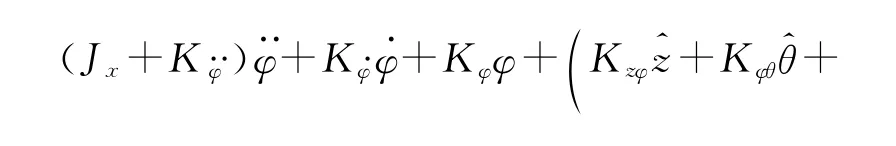
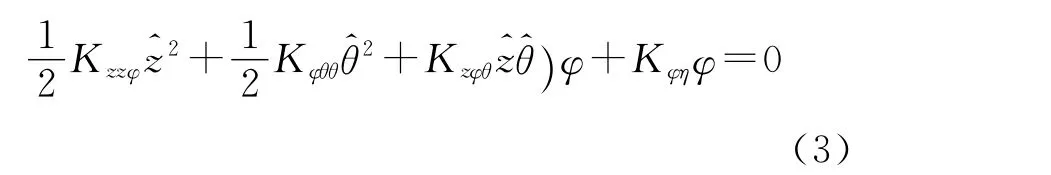
式中：Jx——为横摇惯性矩系数；

z、θ——是升沉和纵摇的线性响应。

η代表波浪，有关参数激励的系数K都与水线面几何性质的微分有关，阻尼系数Kφ·可以由半经验程序得到或者由横摇衰减试验得出，水动力系数利用三维平板的方法来确定。

S.Ribeiro e Silva、T.Santos和 C.Guedes Soaves［8］考虑了甲板入水和船舶复原力矩非线性项的影响，在时域内运用了非线性的五自由度（横荡、升沉、横摇、纵摇、首摇）船舶运动的数值模型：

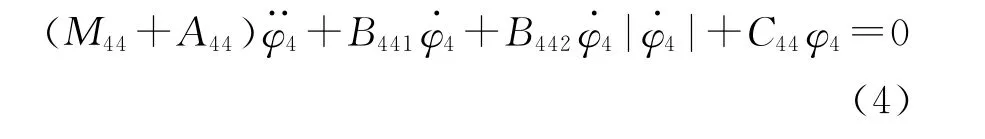
式中：M44+A44——横摇惯性矩系数；

B441——线性阻尼系数；

B442——二次方阻尼系数，可以通过船模自由衰减试验获得；

C44——复原力矩系数。

横摇方程中的未知项可以采用船模试验和静水力计算的方法确定［9～10］。

另外，Jerzy Matusiak［11］运 用 了 二 阶 方 法（two-stage approach）处理参数横摇的非线性模型问题。Naoya Umeda和 Hirotada Hashimoto［12］等人认识到傅汝德-克雷洛夫方法在模拟参数横摇时会过高估计波浪对横摇复原力矩的影响，也会高估参数横摇导致船舶倾覆的危险。

2 基于ITTC模型的参数横摇数值模拟

ITTC对顶浪情况下规则波中船舶的参数横摇方程提出了建议：

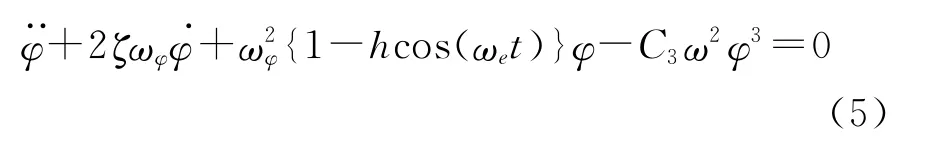
式中：ζ——横摇阻尼比；

C3——复原力矩系数；

ωz——遭遇频率；

h——GM的相对变化值。

方程中的横摇阻尼系数可采用船模试验或半经验公式确定。Subrata Chakrabarti［13］提出总阻尼由等效线性阻尼项来估计：

式中：Beq——等效线性阻尼系数。

阻尼系数成分如下：Bf是船体摩擦阻尼，Be是船体漩涡阻尼，Bw是自由表面兴波阻尼，BL是升力阻尼，BBK是舭龙骨阻尼。

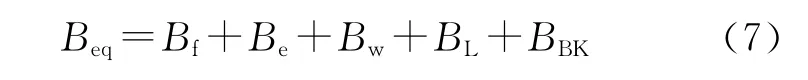
在无船速和有船速两种情况下公式（7）中各成分都有相应的估算表达式。

波浪中复原力臂的变化可采用压力积分法［9］、快速模拟法［14］等多种方法确定。快速模拟法将船体剖面船宽，相对于龙骨线的剖面惯性矩和剖面面积因瞬时水线的变化用平均吃水T（x）处的泰勒级数来表示：

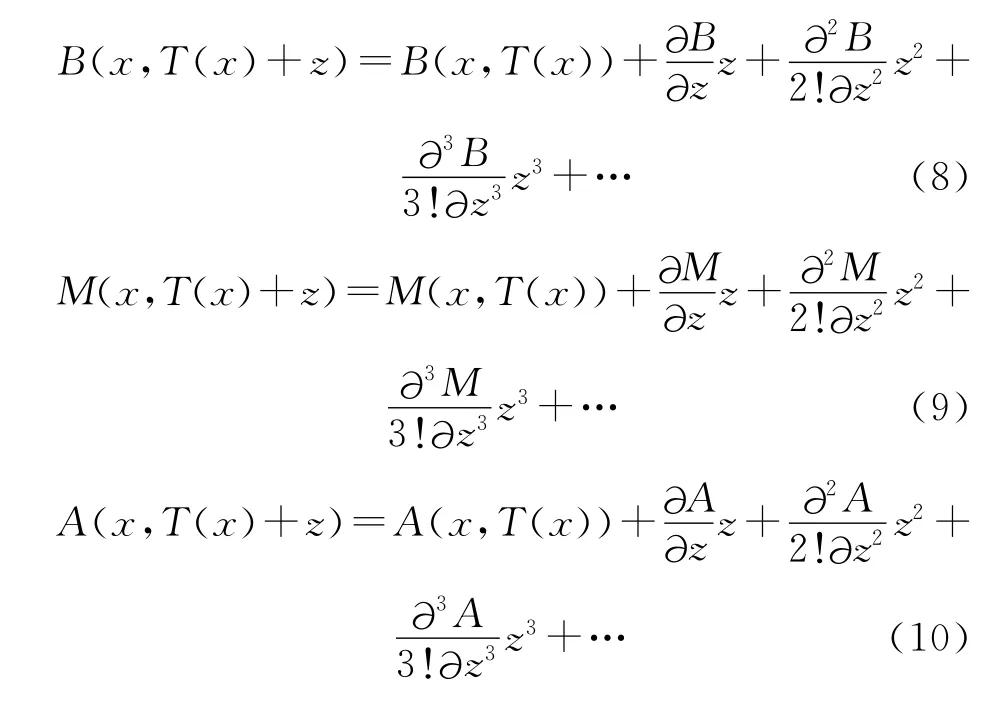
式中：z——表示剖面水线变化的变量。

用r（x，t）（船相对于波浪表面的相对运动）来代替变量z，它可以由升沉和纵摇的传递函数［15］求得。最后，在纵向规则波或不规则波中船舶的GM变化可表示如下：

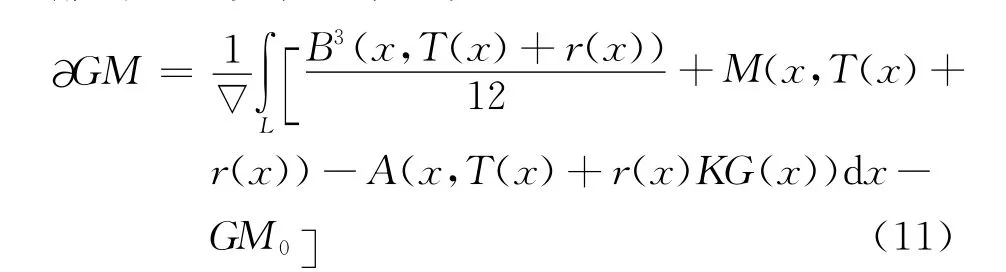
其中：KG（x）——剖面重心，

KG（x）＝KG+x·（η5-atrim）

η5——波浪引起的纵摇角；

atrim——静水中的纵倾角。

3 实例分析结果

将基于ITTC数学模型的参数横摇预报方法应用于一艘滚装船模型，参数横摇的实验在意大利INSEAN船模实验室完成［5］。船模主要参数参考表1。

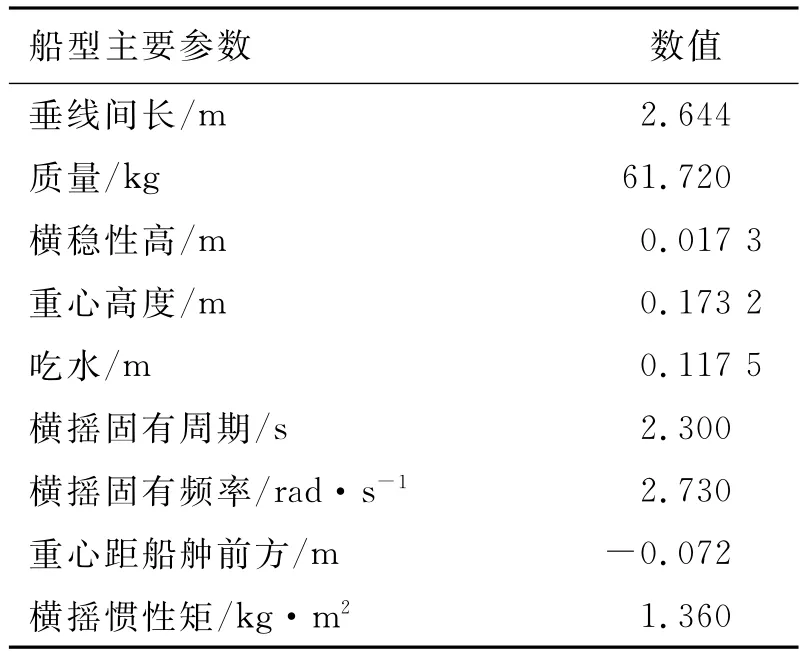
表1 滚装船模型主要参数

数值模拟和水池试验均针对三种规则波：波陡Sw＝，波长和船长比为0.750，0.932，1.000。在每一种规则波条件下，以若干航速点进行模拟和试验，同时采用ITTC解析公式进行验证，对比结果分别列于图1中。在数值模拟时，采用四阶／五阶龙格-库塔算法，初始横摇角取为2°，给定的初始横摇角并不影响后期的谐摇运动幅值，只是缩短了发生参数横摇运动的时间［11］。

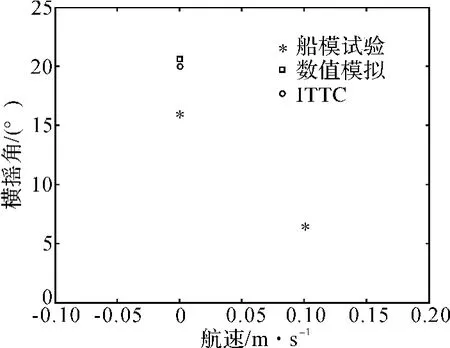
图1 波陡，波长船长比0.75的横摇角

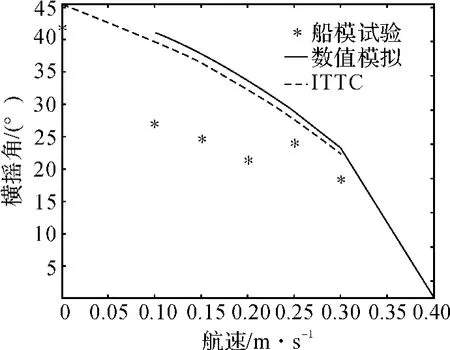
图2 波陡，波长船长比0.932的横摇角

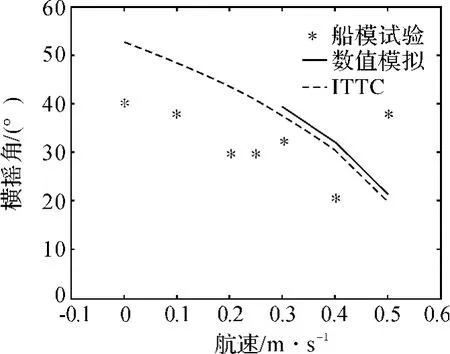
图3 波陡，波长船长比1的横摇角

4 结论

从数值模拟结果与实验数据的对比可以看出：本文所采用的数学模型和算法对于规则波中参数横摇的预报是准确有效的。

由于此方法是基于傅汝德-克雷洛夫假设的，高估了GM变化以及最终的横摇幅值，验证了最近Umeda等人的结论。

与其他方法比较，本文方法应用简单，计算快速。在设计初期，只需要知道船舶的主要参数和型线即可模拟参数横摇，避免谐摇现象的发生。但是当较大时或者波高较高时，预报结果比试验数据偏高，预报准确性仍有待提高。

［1］France W N，Levadou M，Treakle T W，etc.An Investigation of Head-Sea Parametric Rolling and its Influence on Container Lashing Systems［J］.Society of Naval Architects and Marine Engineers，2001.

［2］Umeda N，Hashimoto，H，etc.Nonlinear Dynamics on Parametric Roll Resonance With Realistic Numerical Modeling［J］.Int.Shipbuild.Progr.，51，no.2／3（2004），pp205-220.

［3］巴塔查雅.海洋运载工具动力学［M］.北京：海洋出版社，1982.

［4］Bulian G.，Nonlinear parametric rolling in regular wavesageneral procedure for the analytical approximation of the GZ curve and its use in time domain simulations［J］.Ocean Engineering，2005，pp309-330.

［5］Francescutto A.，Bulian G.Lugni C Nonlinear and stochastic aspects of parametric rolling modeling［J］.Proceedings of 6th International Workshop on Ship Stability，Webb Institute，New York，October 2002：74-81.

［6］Bulian G.，Francescutto A.，Lugni C.，On the Nonlinear Modeling of Parametric Rolling in Regular and Irregular Waves［J］.Int.Shipbuild.Progr.，51，no.2／3（2004），pp173-203.

［7］Marcelo A S.NEVES，Nelson A.PéREZ，Osvaldo Lorca etc.Hull Design Considerations for Improved stability of Fishing Vessels In Waves［C］.8th International Conference on the Stability of Ships and O-cean Vehicles，2003：291-304.

［8］Ribeiro e Silva S.，Santos T.，Guedes Soaves.C.，Time Domain Simulations of A Coupled Parametrically Excited Roll Response in Regular and Irregular Head Seas［C］.8th International Conference on the Stability of Ships and Ocean Vehicles，2003，pp349-360.

［9］Schalck S.，Baatrup J.，Hydrostatic Stability Calculations By Pressure Integration［J］.Ocean Engineer-ing，1990，17（）：155-169.

［10］Radwan A.M.，A Different Method to Evaluate the Intact Stability of Floating Structures［J］.Marine Technology，1938，20（1）：21-25.

［11］Matusiak J.On the Effects of Wave Amplitude，Damping and Initial Conditions On the Parametric Roll Resonance［C］.8th International Conference on the Stability of Ships and Ocean Vehicles，2003：341-347.

［12］Umeda N.，Hashimoto H.，Nonlinear analysis of parametric rolling in longitudinal and quartering seas with realistic modeling of roll-restoring moment［J］.Journal of Marine Science and Technology，2004：117-126.

［13］Subrata Chakrabarti，Empirical calculation of roll damping for ships and barges［J］.Ocean Engineering，2001：915-932.

［14］Hua Jianbo，Fast Simulation of Nonlinear GM-Variation of a Ship in Irregular Waves［J］.Journal of Ship Mechanics，2000，4（3）：25-35.

［15］Jensen J J，Mansour A E，Olsen A.S.，Estimation of ship motions using closed-form expressions［J］.O-cean Engineering，2004：61-85.