怎样解开放型画图题

顾劲松　石灿辉

为了考查同学们用数学知识解决实际问题的能力，近几年中考数学题中频频出现一种新题型———开放型画图题．这类问题的答案往往不止一个，需多角度进行探索、猜想和论证，才能把所有的符合条件的图形作出来，因而能很好地培养我们的创新思维及动手能力．现以中考题为例，说明这类问题的解法．

例１探究规律：

如图１所示，已知：直线ｍ∥ｎ，Ａ、Ｂ为直线ｎ上两点，Ｃ、Ｐ为直线ｍ上两点．

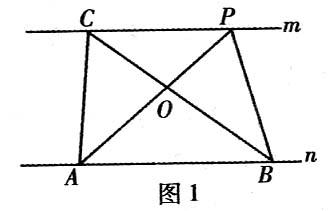
（１）请写出图中面积相等的各对三角形：_________；

（２）如果Ａ、Ｂ、Ｃ为三个定点，点Ｐ在ｍ上移动，那么，无论Ｐ点移动到任何位置，总有_________与△ＡＢＣ的面积相等．

理由是：_________．

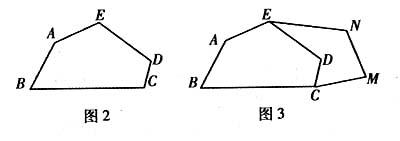
解决问题：

如图２所示，五边形ＡＢＣＤＥ是张大爷十年前承包的一块土地的示意图．经过多年开垦荒地，现已变成如图３所示的形状，承包土地与开垦荒地的分界小路（即图３中折线ＣＤＥ）还保留着．张大爷想过Ｅ点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多，右边的土地面积与开垦的荒地面积一样多．请你用有关的几何知识，按张大爷的要求设计出修路方案．（不计分界小路与直路的占地面积）

（１）写出设计方案，并画出相应的图形；

（２）说明方案设计理由．

解：探究规律：（１）△ＡＢＣ和△ＡＢＰ，△ＡＯＣ和△ＢＯＰ，△ＣＰＡ和△ＣＰＢ．

（２）△ＡＢＰ．

平行线间的距离相等，无论点Ｐ在ｍ上移动到任何位置，总有△ＡＢＰ与△ＡＢＣ同底等高，因此，它们的面积总相等．

解决问题：（１）连接ＥＣ，过点Ｄ作ＤＦ∥ＥＣ，交ＣＭ于点Ｆ，连接ＥＦ，ＥＦ为所求直路的位置．画法如图４所示．

（２）设ＥＦ交ＣＤ于点Ｈ，由上面结论可知：Ｓ_△ＥＣＦ＝Ｓ_△ＥＣＤ，Ｓ_△ＨＣＦ＝Ｓ_△ＥＤＨ．

∴Ｓ_{五边形ＡＢＣＤＥ}＝Ｓ_{五边形ＡＢＣＦＥ}，Ｓ_{五边形ＥＤＣＭＮ}＝Ｓ_{四边形ＥＦＭＮ}．

评析：本题的探究规律可直接运用课本知识求解，比较容易．它是解决后续问题的基础和条件．接着的解决问题比较困难，解决问题的关键是把实际问题化成数学问题．其实在探究规律中已有了明确提示，就是把这个问题看作是同底等高（面积不变）的三角形变换．

例２有一长方形餐厅，长１０米，宽７米，现只摆放两套同样大小的圆桌和椅子，一套圆桌和椅子占据的地面部分可看成半径为１．５米的圆形（如图５所示）．在保证通道最狭窄处的宽度不小于０．５米的前提下，此餐厅内能否摆下三套或四套同样大小的圆桌和椅子呢？请在摆放三套或四套的两种方案中选取一种，画出设计示意图．

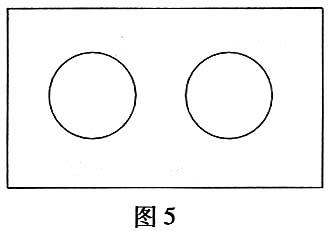
提示：①画出的圆应符合比例要求；

②为了保证示意图的清晰，请你在有把握后才将设计方案画在方格纸上．

说明：画出符合要求的三个圆得５分，四个圆得８分．

解：摆放三套与四套的设计方案参考示意图如图６、图７所示．

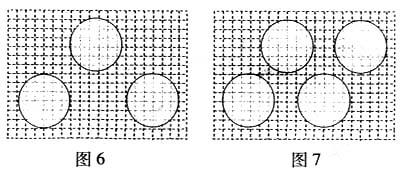
评析：这种类似游戏性质的画图问题，不仅能激发我们的学习兴趣，而且还有相当的实用价值，进行这方面的练习，有助于培养观察能力、动手能力以及创造能力．此题虽然简单，但如忽视题中的附加条件（通道最狭窄处的宽度不小于０．５米），也容易造成构图错误．

例３如图８，现需测量一井盖（圆形）的直径，只有一把角尺（尺的两边互相垂直，一边有刻度，且两边长度都长于井盖半径）．请结合图形用文字说明测量方案，写出测量步骤（要求写出两种测量方案）．

分析：这道开放性几何作图题的解法很多，仅列举以下３种解法．

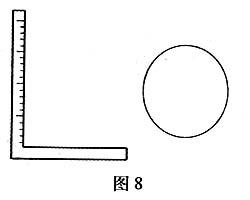
解法１：如图９，把井盖卡在角尺间，尺与井盖交于点Ｂ，可测得ＡＢ的长度，井盖的直径为２ＡＢ．

设井盖所在圆的圆心为Ｏ，连接ＯＣ、ＯＢ，由切线的性质得ＡＣ＝ＡＢ，又ＯＣ⊥ＡＣ，ＡＢ⊥ＡＣ，ＯＢ＝ＯＣ，则四边形ＡＢＯＣ为正方形．

解法２：如图１０，把角尺顶点Ａ放在井盖边缘，记角尺一边与井盖边缘交于点Ｂ，另一边与井盖边缘交于点Ｃ（若角尺另一边无法达到井盖边上，把角尺当直尺用，延长另一边与井盖边缘交于点Ｃ），度量ＢＣ长即为直径．

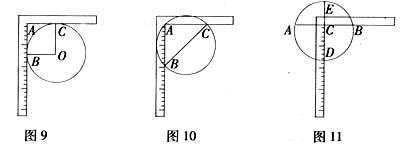
解法３：如图１1，把角尺当直尺用，量出ＡＢ的长度，取ＡＢ中点Ｃ，然后把角尺顶点与Ｃ点重合，一边与ＣＢ重合，让另一边与井盖边交于Ｄ点，延长ＤＣ交井盖边于Ｅ，度量ＤＥ长度即为直径．

评析：这道题是一道把几何计算、论证与画图结合的好题，考查了同学们综合运用几何知识解决实际问题的能力．