TBM常截面盘形滚刀破岩过程受力研究

摘要：

针对目前工程上常用的常截面盘形滚刀受力分析问题，应用有限元方法建立了滚刀破岩的三维旋转切割模型，模拟滚刀破岩过程。通过计算得出常截面盘形滚刀破岩时的切削力，并与实验数据和文献数据进行比较，结果表明模拟的滚刀切削力与实际情况较为吻合，验证了仿真模拟的可靠性。同时，滚刀破岩掘进试验结果表明，所测滚刀垂直力随时间变化曲线与仿真结果一致，呈波动特征，且滚刀切削力试验值与仿真数据误差较小。进一步将模拟数据与科罗拉多矿业大学（CSM）模型对比，发现整体结果较CSM模型值偏大，但与实验值更接近。通过对仿真模型岩石强度、掘进加载速率、刀刃宽度3个因素进行参数敏感性分析，得出在相同贯入度下，垂直力随上述因素的增大而提高，但掘进加载速率对垂直力的影响较小。相关成果可为TBM隧道的掘进设计与施工提供参考。

关" 键" 词：

滚刀破岩； 切削力； 有限元； 掘进试验； CSM模型

中图法分类号： U455.3

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2025.01.023

收稿日期：2024-01-19；接受日期：2024-04-17

基金项目：

江苏省基础研究计划（自然科学基金）项目（BK20210721）

作者简介：

李忠艳，女，讲师，硕士，主要从事工程管理方面的研究。E-mail：963624907@qq.com

通信作者：

张雯超，男，讲师，博士，主要从事地下空间与智能交通技术方面的研究。E-mail：anwei1256@126.com

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2025） 01-0173-07

引用本文：

李忠艳，刘杨，张雯超，等.TBM常截面盘形滚刀破岩过程受力研究

［J］.人民长江，2025，56（1）：173-179，204.

0" 引 言

随着中国基础建设的不断发展，隧道建设特别是水利工程面临的工况更复杂、规模更大，施工难度更高，对TBM刀具提出了更高的要求［1］。滚刀作为TBM掘进过程中主要的破岩工具直接作用于被切削体，根据刀刃形式可以分为盘形滚刀与球齿滚刀，按每个刀箱上刀刃数量可以分为单刃滚刀、双刃滚刀及多刃滚刀。对于双刃或多刃滚刀，在破岩时易因受力不均而造成磨损，一般不适用于硬岩。因此，在刀盘空间布置容许的情况下，单刃盘形滚刀是最常用的破岩工具之一。在破岩过程中，滚刀与掌子面岩石直接接触的部位是刀圈，其直接影响破岩效果及施工效率。盘形滚刀按刀圈截面形状可以分为3类：尖刃截面、楔形截面和近似常截面。尖刃截面易侵入岩石，但刀刃容易钝化；楔形截面在切削硬岩条件下，较大荷载同样会造成刀刃磨损过度而钝化。钝化后的刀刃使刀圈与岩石接触面积增加，容易增大刀具荷载。近似常截面盘形滚刀在磨损后接触面积变化较小，在工程中应用较多。

岩石作为一种天然材料，物质成分多样，内部裂纹情况复杂，不具有各向同性，其破坏模式主要分为张拉破坏与剪切破坏［2］。滚刀侵入岩体过程中一般认为滚刀受3个主要外荷载的影响，即滚刀垂直力FN、滚刀滚动力FR、滚刀侧向力FS。在切削过程中对于安装倾角为0°的滚刀，其侧向力一般忽略不计。目前对滚刀的受力预测公式按岩石的破坏模式分为基于挤压破坏机理的受力模型和基于挤压-剪切破坏机理的受力模型两类。国内外学者对此进行了大量的理论与实验研究，得出了许多经典的滚刀破岩平均力预测模型。伊万斯建立了尖刃截面盘形滚刀切割岩石垂直力预测公式，认为滚刀垂直力平均值为岩石单轴抗压强度与滚刀和岩石接触面投影面积的乘积，其中投影面积可以看成两条抛物线围成的面积一半进行计算［3］。伊万斯公式将复杂的滚刀破岩受力模型简化，认为只有刀刃正下方的岩石发生挤压破坏，虽然实验表明该公式计算得到的垂直力比实际值小，但其思想为后面学者推导奠定了基础。Roxborough等［4］基于伊万斯公式思想，将岩石接触面投影面积修正为矩形，建立了尖刃截面盘形滚刀垂直力与滚动力计算公式，该模型同样仅考虑了岩石挤压破坏的情况。秋三藤三郎［5］在推导滚刀垂直力时依然采用伊万斯模型，但在侧向力的推导时考虑了岩石剪切破坏，认为尖刃截面盘形滚刀侧向力为相邻滚刀间岩石受剪剥落受到的反作用力。科罗拉多矿业大学模型（CSM）［6］是在滚刀线性切割试验基础上建立的经验受力模型，该模型形式简单，输入参数简单。

Li等［7］融合Roxborough模型和CSM模型提出了滚刀受力预测模型（RCC），对比发现该模型比CSM模型更准确。She等［8］基于岩石的摩尔-库仑破坏准则，建立了恒定截面（CCS）滚刀的切削荷载力学模型，得到滚刀的法向和切向力与岩石力学特性、刀具几何参数和切削参数的定量关系。不难发现，国内外对于滚刀破岩的机理与受力模型预测已有较成熟的研究成果，但是这些模型对于常截面盘形滚刀的受力预测还存在一定误差［9-12］。

在现场与室内试验方面，李克金等［13］对济南市地铁R1线复合地层盾构区间进行了试验研究，使用不同强度试件进行滚刀贯入力学试验，研究发现临界贯入度与贯入速率呈对数关系。韩伟锋［14］对工程岩样开展不同刀间距的破岩试验，分析了不同地质条件下的最优刀间距。随着数值仿真技术的发展与计算机性能的提高，越来越多的学者利用有限元、离散元数值软件针对滚刀破岩机理与受力情况展开了大量的研究。Cho等［15］对滚刀切削岩石进行了三维动态仿真，发现在刀间距一定的情况下，贯入度与刀间距之比存在最优值使比能耗最小。程永亮［16］使用有限元理论，采用扩展的Drucker-Prager模型作为岩石的本构模型，对双滚刀切削岩石的过程进行了三维动态模拟，研究了TBM盘形滚刀的破岩效率及最优贯入度。耿麒等［17］针对“刀下超破、刀间欠破”问题开展了仿真与试验，研究表明当刀间距在60～110 mm范围内变化时，切削比能随刀间距增大呈先减小后增大的规律。

综上所述，随着施工环境的变化和盾构技术的不断发展，新截面滚刀的使用将导致传统滚刀受力模型不适用，给刀具的设计与刀盘掘进参数的设定带来困难。尽管滚刀破岩机理与经典受力模型已有大量的研究，但成果主要集中在“V”字形截面，将其应用于常截面盘形滚刀的受力计算将造成较大误差。本文以目前水利工程TBM中常用的常截面滚刀为研究对象，采用数值模拟与掘进试验的方法分析常截面滚刀受力及其影响，弥补目前研究的不足。另一方面，现阶段基于数值仿真与数据挖掘的研究方法虽得以运用，但研究方法单一，且缺乏普适性的规律，特别是在三维数值仿真方面，主要采用单刀切削。为此，本文基于有限元软件LS-DYNA建立了刀盘+刀具的一体三维旋转切削模型，更贴合实际切削情况，并通过室内掘进试验进行验证，得到常截面盘形滚刀破岩受力规律。

1" 滚刀切削仿真建模

LS-DYNA是一款功能全面的显式动力分析有限元数值分析软件，被广泛应用于爆破、侵彻、冲击等问题的数值模拟中，具有多种单元类型，并且自适应网格划分。因此，本文选取该软件建立常截面盘形滚刀切削岩石的三维模型。

1.1" 模型参数设置

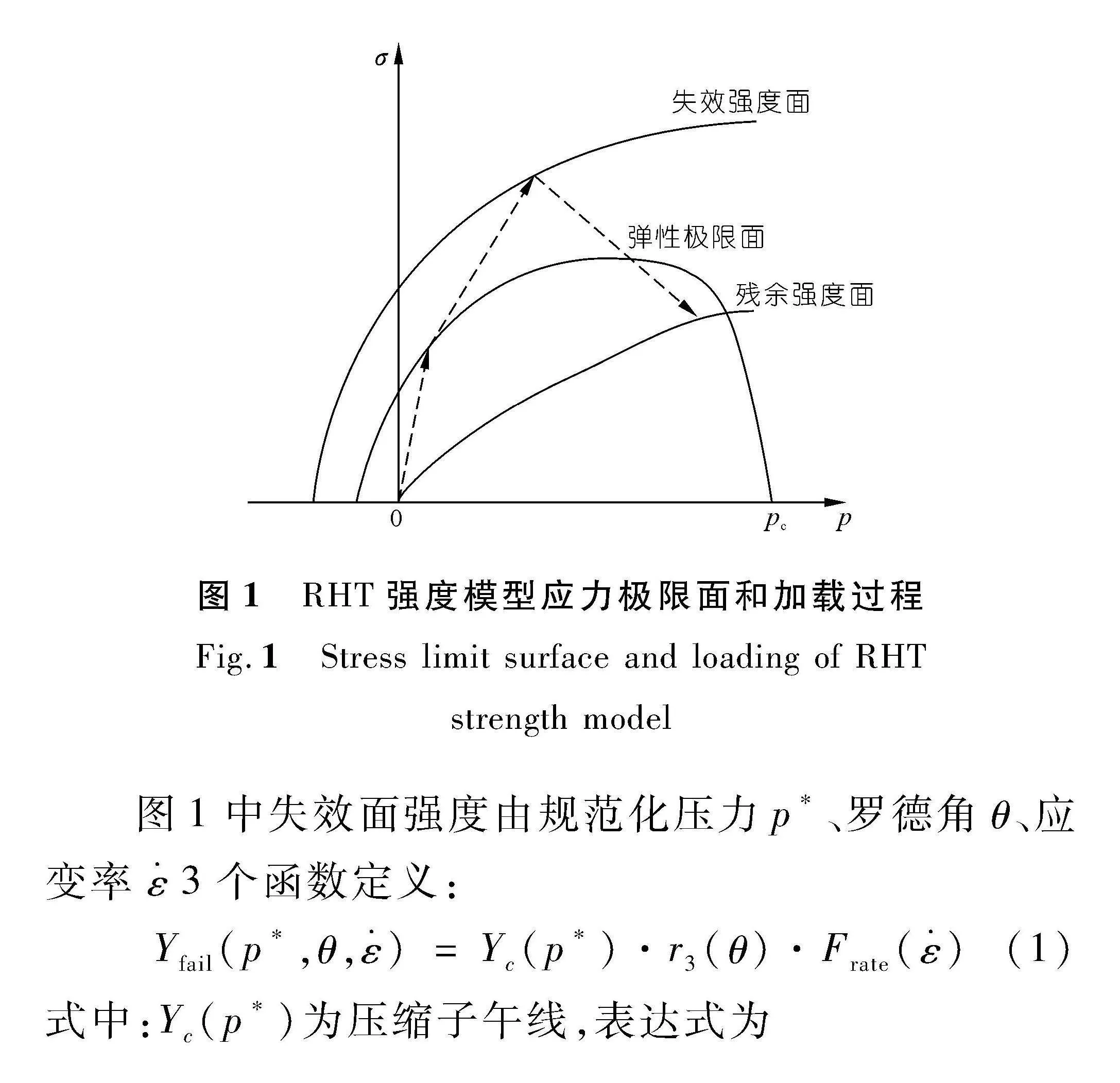
参考文献［18］，采用RHT模型描述岩石、混凝土类材料的初始屈服强度、失效强度及残余强度的变化。该模型有3个极限面，即弹性极限面、失效强度面和残余强度面，如图1所示。

图1中失效面强度由规范化压力p、罗德角θ、应变率ε· 3个函数定义：

Yfail（p，θ，ε·）=Yc（p）·r3（θ）·Frate（ε·）（1）

式中：Yc（p）为压缩子午线，表达式为

Yc（p）=fc［A·（p-pspall·Frate（ε·））N］（2）

式中：层裂强度pspall=ft/fc，ft为岩石单轴抗拉强度，fc为岩石单轴抗压强度；A，N为与混凝土有关的常数；Frate（ε·）为动力增强因子。

另，

r3（θ）=r/rc=2（1-ψ2）cosθ+（2ψ-1）4（1-ψ2）cos2θ+5ψ2-4ψ4（1-ψ2）cos2θ+（1-2ψ）2

（3）

式中：r3（θ）为混凝土失效强度与偏应力张量第二不变量J2、第三不变量J3及静水压力有关的实验结果；θ是关于偏应变张量第二、三不变量的函数

θ=13arccos33J32J1/22，0≤θ≤π3（4）

ψ=rt/rc

拉压子午线情况下满足：θ（0）=ψ，θπ3=1。

其中，rt是拉子午线处的偏应力，rc为压子午线处的偏应力。

图1中弹性极限面强度函数为

Yela=Yfail（p/Fela）·Fela·Fcap（p）（5）

Fcap=0，p≥p0/fc1-p-1/3p0/f-1/3" ，13＜p＜p0fc1，p≤1/3（6）

式中：p0为弹性强度极限值，Fela为材料弹性强度与极限强度之比，Fcap为应变率强化因子。

图1中残余强度面函数为

Yres=B·（p）M·［sgn（p）+1］/2（7）

式中：B和M为常数，符号函数sgn（p）=-1plt;00p=01pgt;0。

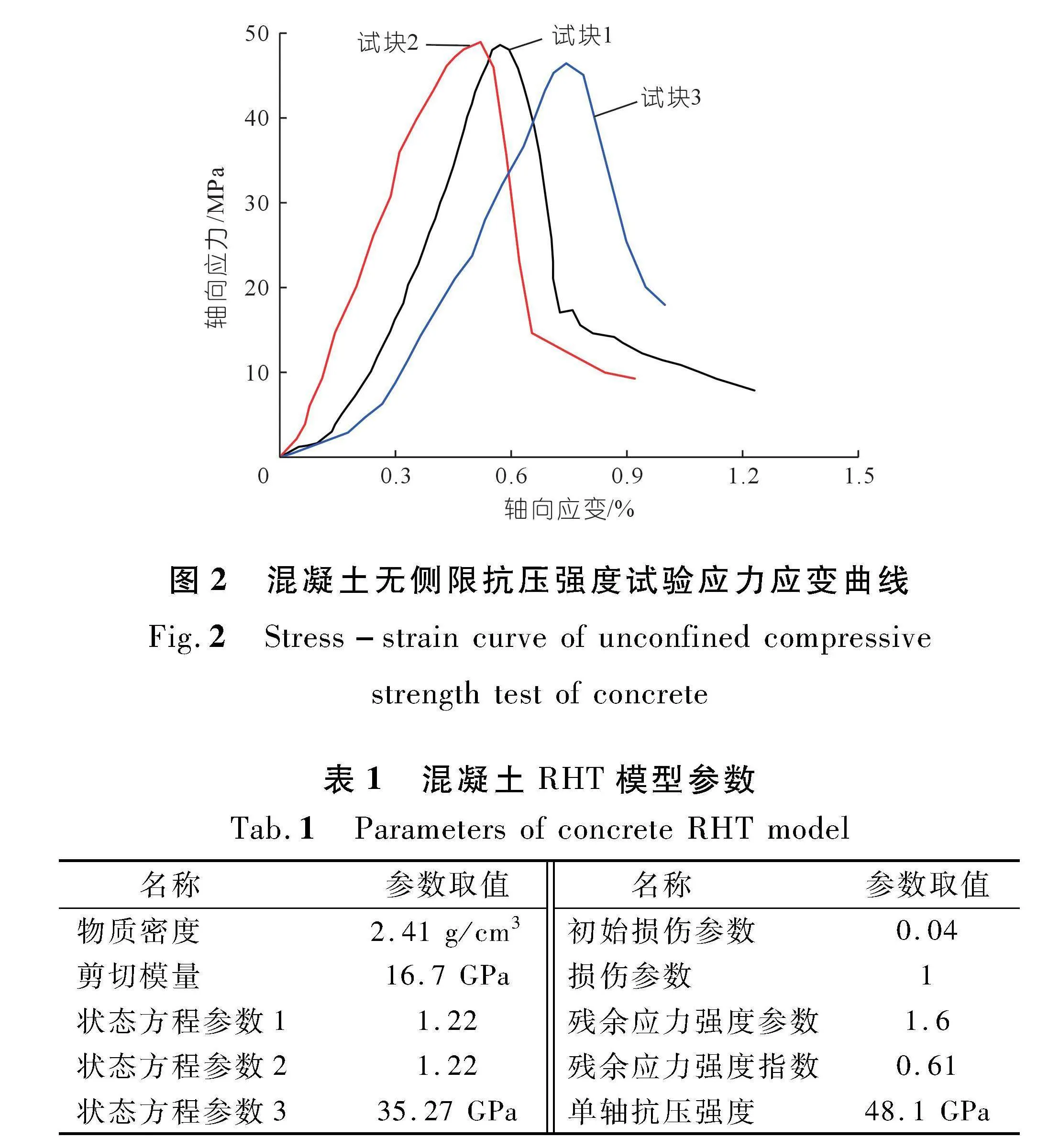
本文开展了试验混凝土材料的力学性质试验，此处试样与后文掘进试验具有一致性。混凝土无侧限抗压强度试验的轴向应力-应变曲线如图2所示。取平均值计算得出试验模拟材料的无侧限抗压强度为48.1 MPa。结合力学性质试验参数与有关文献［18］，模型主要材料参数如表1所列。

为了节省计算时间并简化模型，在不考虑刀具磨损变形的情况下，滚刀采用刚体材料，并仅对刀圈部位进行建模，其模型参数如下：物质密度为8 g/cm3，剪切模量为210 GPa，泊松比为0.25。

1.2" 切削模型的建立

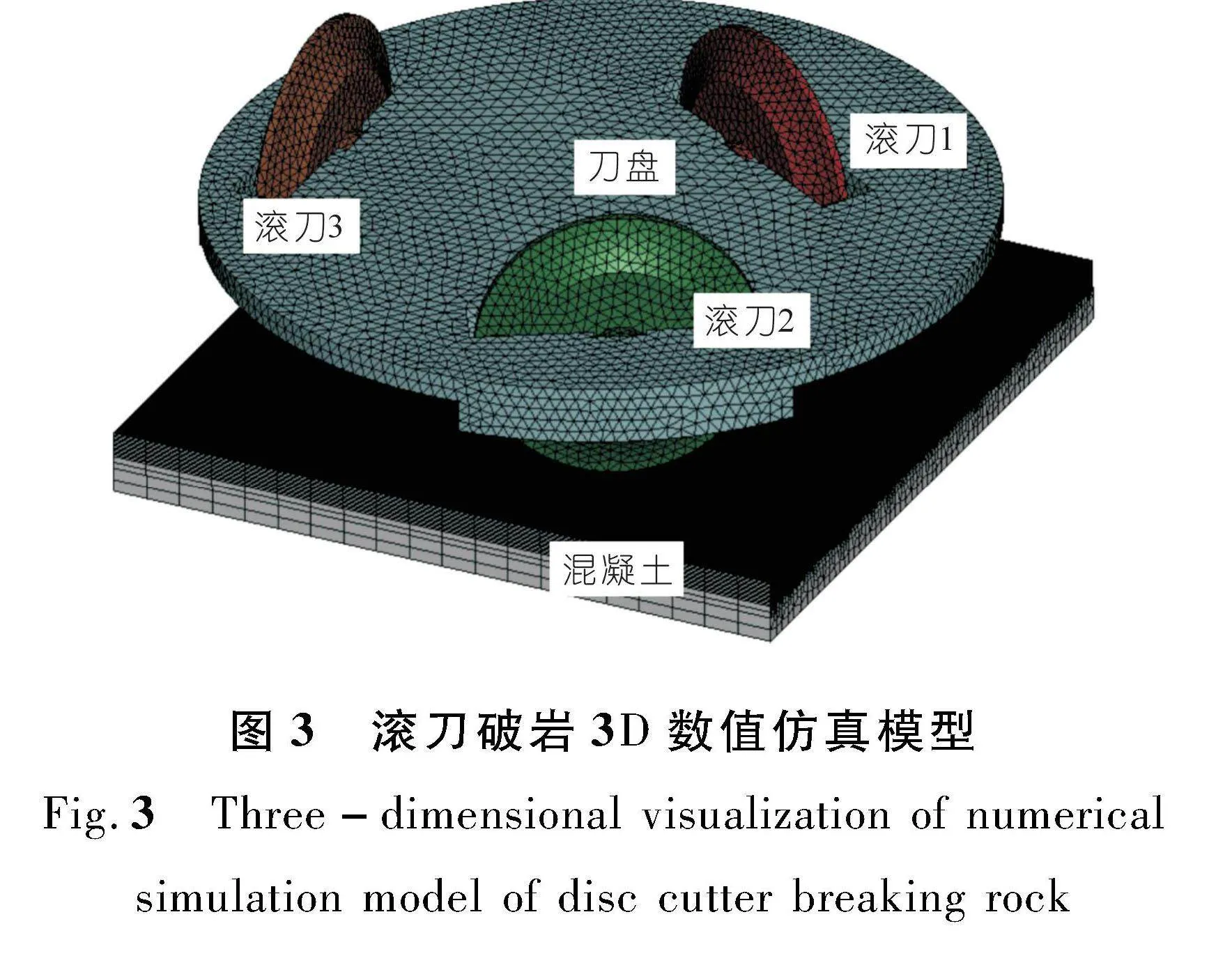
滚刀刀盘切削岩样模型如图3所示。其中刀盘采用四面体网格划分，混凝土采用六面体网格，对上层混凝土进行网格加密。混凝土模型尺寸为1 100 mm×1 100 mm×100 mm。为了最大限度模拟实际工程情况，约束混凝土底部节点各个方向的位移及转动，四周节点定义为无反射边界条件。在切削过程中，混凝土表现为明显的非线性破坏。因此，刀具混凝土之间采用面-面侵蚀接触。

建立直径为1 200 mm的刀盘模型，分别以378，462，562 mm为极径，建立3个滚刀模型，滚刀采用直径为432 mm的标准17英寸常截面盘形滚刀，刀刃宽度为15 mm。为简化计算将滚刀与刀盘固定限制其自转，刀盘做2 r/min的圆周运动，并以20 mm/min的掘进速度向混凝土方向推进。

2" 仿真结果分析

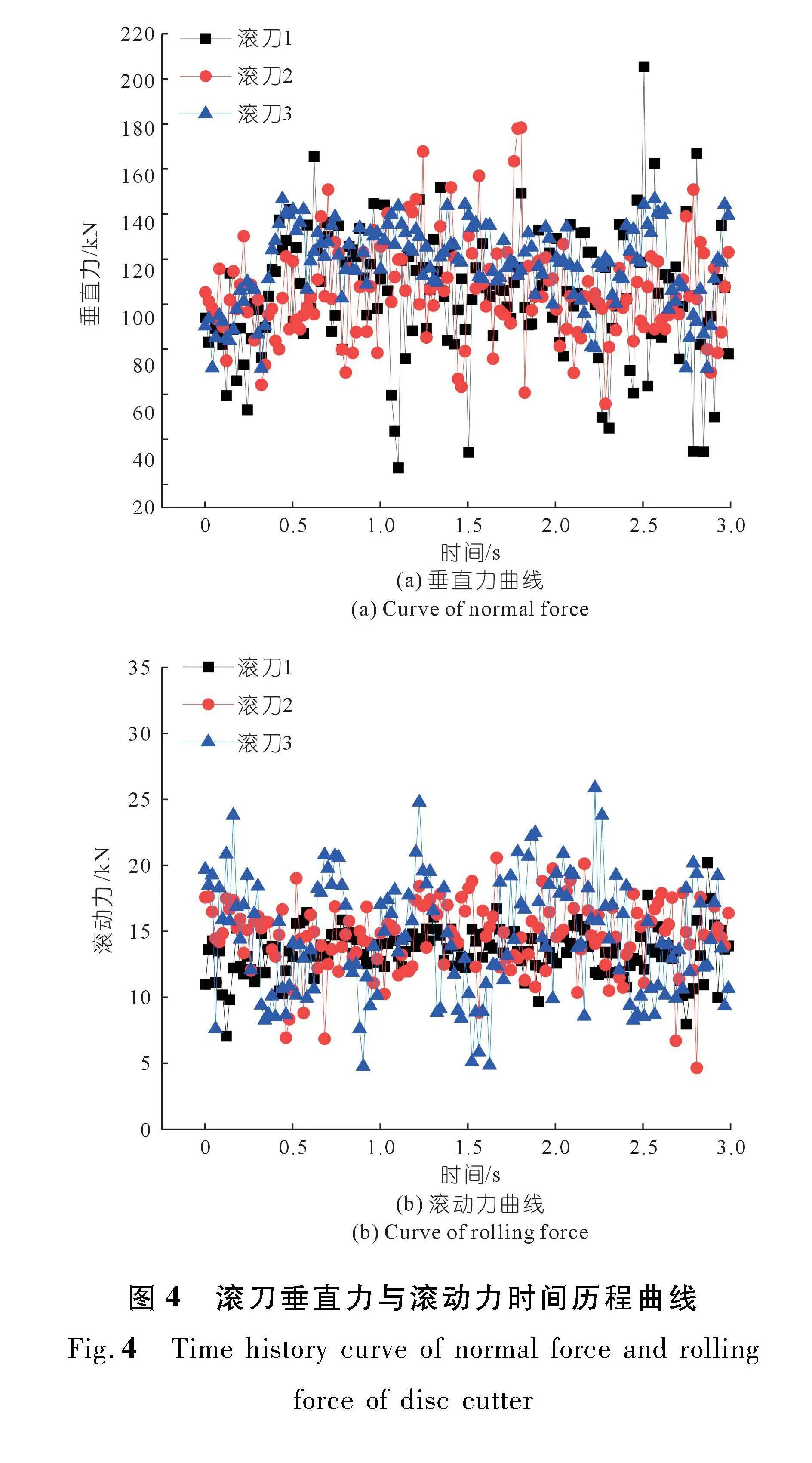
由于滚刀刚接触碾压混凝土时的情形与实际情况存在差距，因此选取滚刀进入稳定切削后3 s内的切削力数据进行分析，导出滚刀的垂直力与滚动力曲线，如图4所示。由稳定段滚刀荷载曲线可知，垂直力基本在30～210 kN波动，滚动力基本在5～25 kN波动，荷载的波动反映了岩石类材料在破坏过程中是跃进式的，这与滚刀破岩机理中密实核的存在有关。经计算，3把滚刀平均垂直力分别为104.3，107.1，116.6 kN，平均滚动力分别为13.51，14.41，15.23 kN。滚刀平均垂直力与滚动力略有增加，主要是由滚刀刀间距与相对切削速度增大所致。

3" 掘进试验

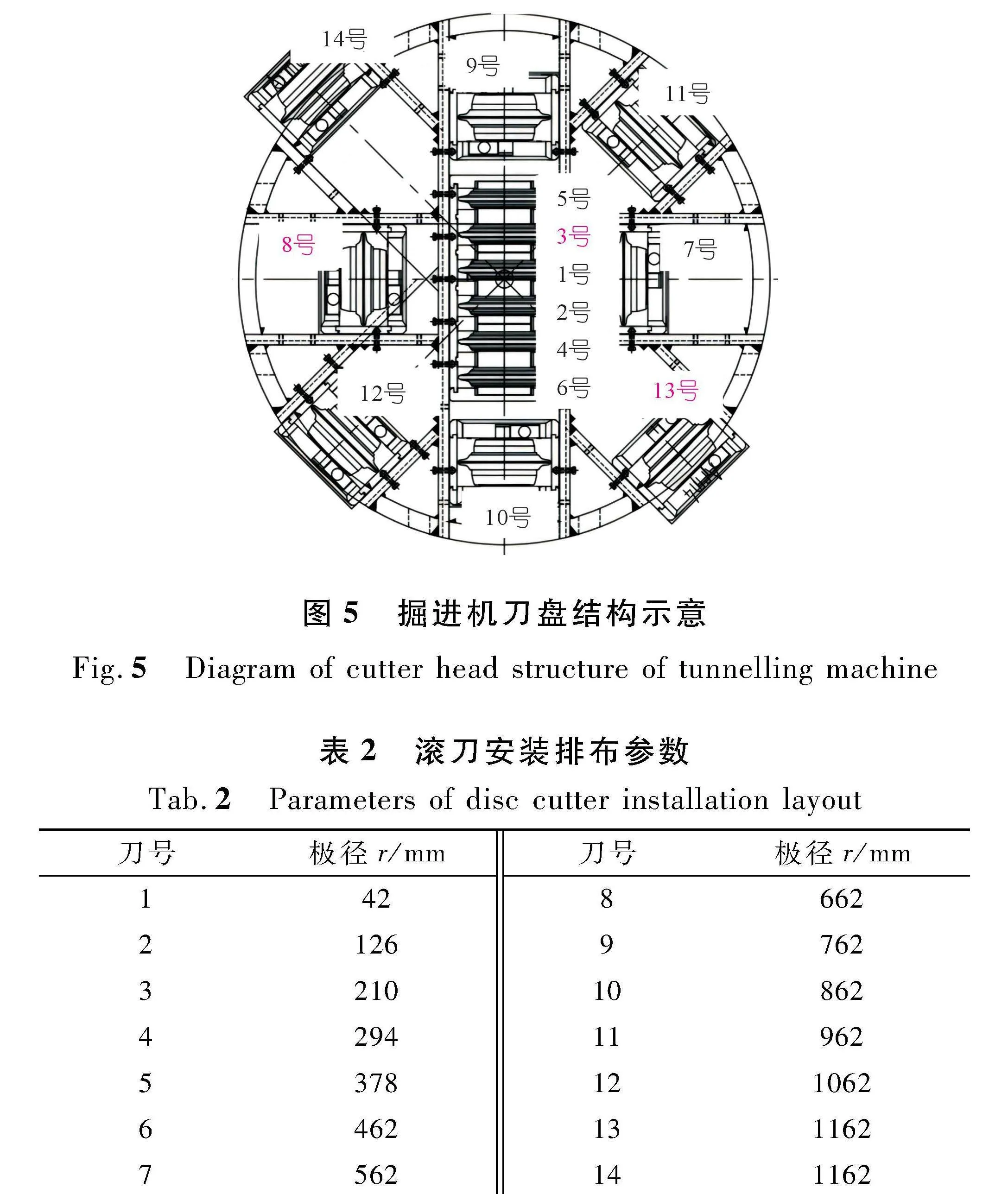
采用TBM刀盘掘进性能试验平台开展常截面盘形滚刀破岩试验，掘进机刀盘结构如图5所示。试验刀盘直径为2.280 m，驱动转速为0～6 r/min，最大总推力400 t，装备扭矩为250 kN·m。刀盘面板可安装3把中心双刃刀具和8把单刃刀具，刀间距调整范围为80～100 mm。试验共配置14把直径为432 mm的17寸常截面盘形滚刀，其中1～6号刀具为3把刀间距84 mm的中心双刃滚刀，7～14号为8把刀间距为100 mm的单刃滚刀。滚刀安装排布参数见表2。

3.1" 试验方案

试验采用C45号混凝土作为样本代替天然岩样。将购置的商用混凝土灌注至试验平台岩箱内振捣均匀，标准养护14 d，并留取样本浇筑标准混凝土试块。试验前测试混凝土试块无侧限抗压强度。试验平台布置多个传感器，操作平台控制面板可对刀盘转速、进尺、推力和扭矩进行实时记录。

设定掘进平台刀盘转速为2 r/min，掘进速度为20 mm/min。推进刀盘将掌子面混凝土碾磨均匀。在整个试验过程中，可获取分析的数据有：① 刀盘的实时掘进数据；② 刀盘的推力、扭矩；③ 14把滚刀的垂直力。

3.2" 试验结果分析

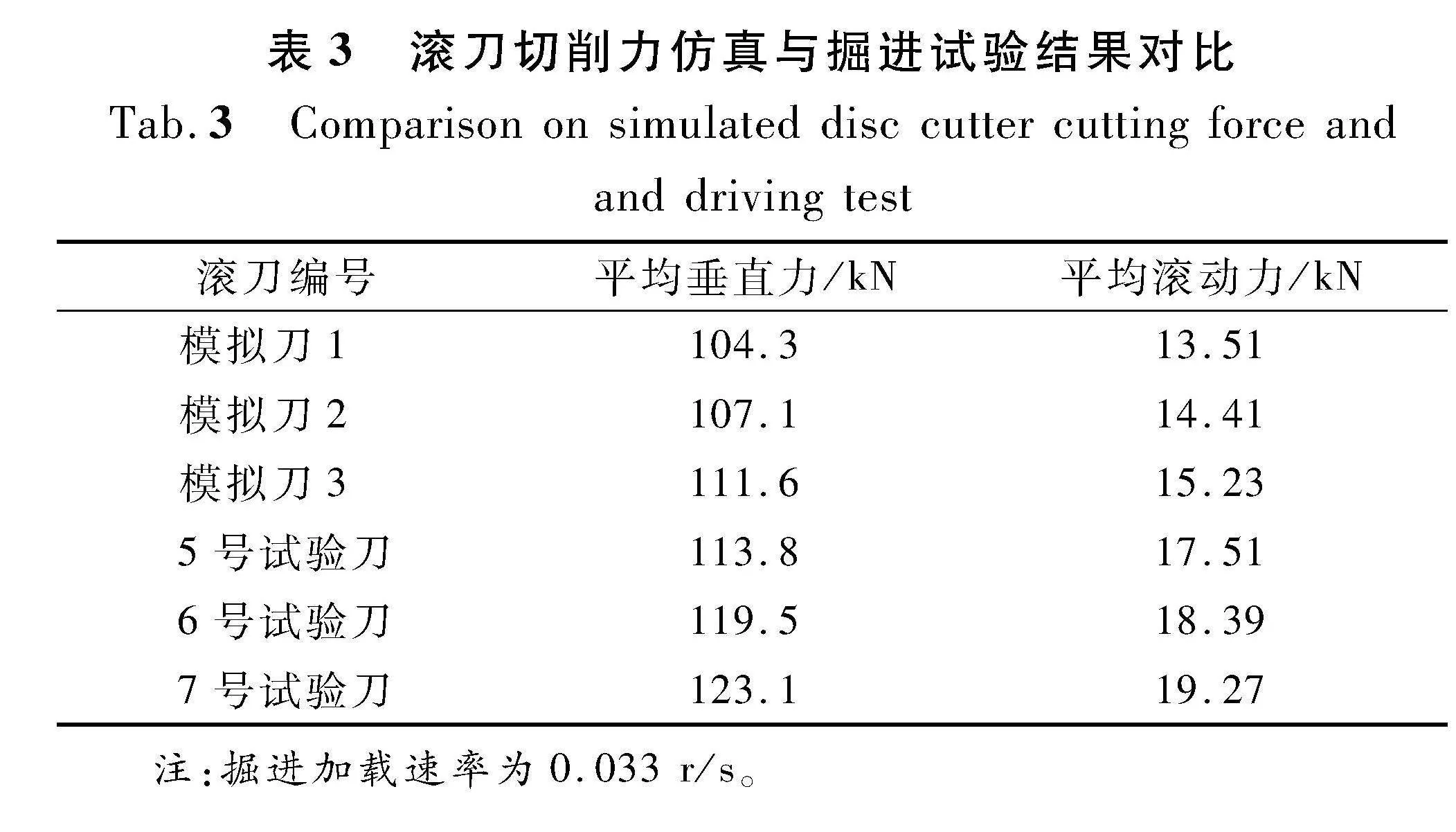
由于掘进过程中有14个刀刃进行破岩，选取与仿真环境相近的5，6，7号3把滚刀作为研究对象，分析破岩切削力，并与仿真结果对比验证。取切削稳定后60 s数据进行研究，3把滚刀的垂直力随时间变化曲线如图6所示。由图6可知，滚刀的垂直力曲线与本文仿真结果接近，总体上在40～180 kN波动。由于数值滚刀切削力采集频率比试验高，因此切削力曲线数值比试验波动更大。由于试验设备条件限制，对于滚刀滚动力的获取可通过切削系数C一致性这一原则确定，如式（8）所示：

C=Tni=1Fn·rn（8）

式中：T为刀盘平均扭矩；Fn为第n把滚刀的平均法向力；rn为滚刀安装极径。

计算试验过程中3把试验刀的平均垂直力与平均滚动力，结果如表3所列。由表3可知，随着滚刀安装极径的增大，垂直力与滚动力同样增大，这是因为切削力随刀间距与切削速度的增大而增加。由于模拟过程中对滚刀的运动进行了简化，模拟值与试验值存在差异。模拟刀的平均滚动力比试验刀略小，但在合理范围之内。综合掘进试验的结果，验证了本文仿真结果的可靠性。

4" 结果分析

4.1" 模型验证

CSM模型是在线性切割模型基础上与众多学者理论相结合得出的一种实用预测模型［6］，滚刀垂直力FN、滚刀滚动力FR的计算如式（9）～（10）所示。

FN=CφRT1+ψSσ2cσtφRT13cosφ2（9）

FR=CφRT1+ψSσ2cσtφRT13sinφ2（10）

式中：C为无量纲系数，取2.12；R为滚刀半径；φ为滚刀与岩石接触角，φ=arccosR-hR，h为滚刀侵入深度；T为刀刃宽度；ψ为刀尖压力分布系数，ψ=-0.2～0.2；S为刀间距；σc为岩石的抗压强度；σt为岩石的抗剪强度。

赵海雷等［19］根据三角函数的泰勒展开式将CSM模型公式进一步简化为（11）～（12）：

FN=0.8T5/6S1/3σch1/3（11）

FR=0.8T5/6S1/3σch5/6（12）

通过改变仿真模型的贯入度，获取不同贯入度下滚刀的垂直力切削曲线。取3把试验滚刀的平均值，分别计算不同贯入度下滚刀垂直力值。将仿真数据与CSM模型进行对比，如图7所示。由图7可以看出，虽然仿真数据与CSM模型计算得到的数据规律一致，随贯入度的增加而增大，但通过CSM模型计算得出的结果比仿真结果小，且差距较大。因此，传统的滚刀破岩模型与现阶段使用的常截面盘形滚刀破岩实测值存在一定的差值，这也是本文研究的目的所在。

为了进一步确定本文数值仿真的可靠性，选取国内外文献中与本文工况相似的试验与仿真数据进行对比，如表4所列。由于滚刀的切削力受岩石强度、刀具类型、掘进参数、贯入度等多个因素的影响，因此本文选取的文献数据会存在一定偏差，但参数大致与本文相似。表中，

引入掘进加载速率ε来表征滚刀切削时的掘进参数，其值由刀盘转速决定，如式（13）所示：

ε=N/60（13）

式中：N为转速，r/s。

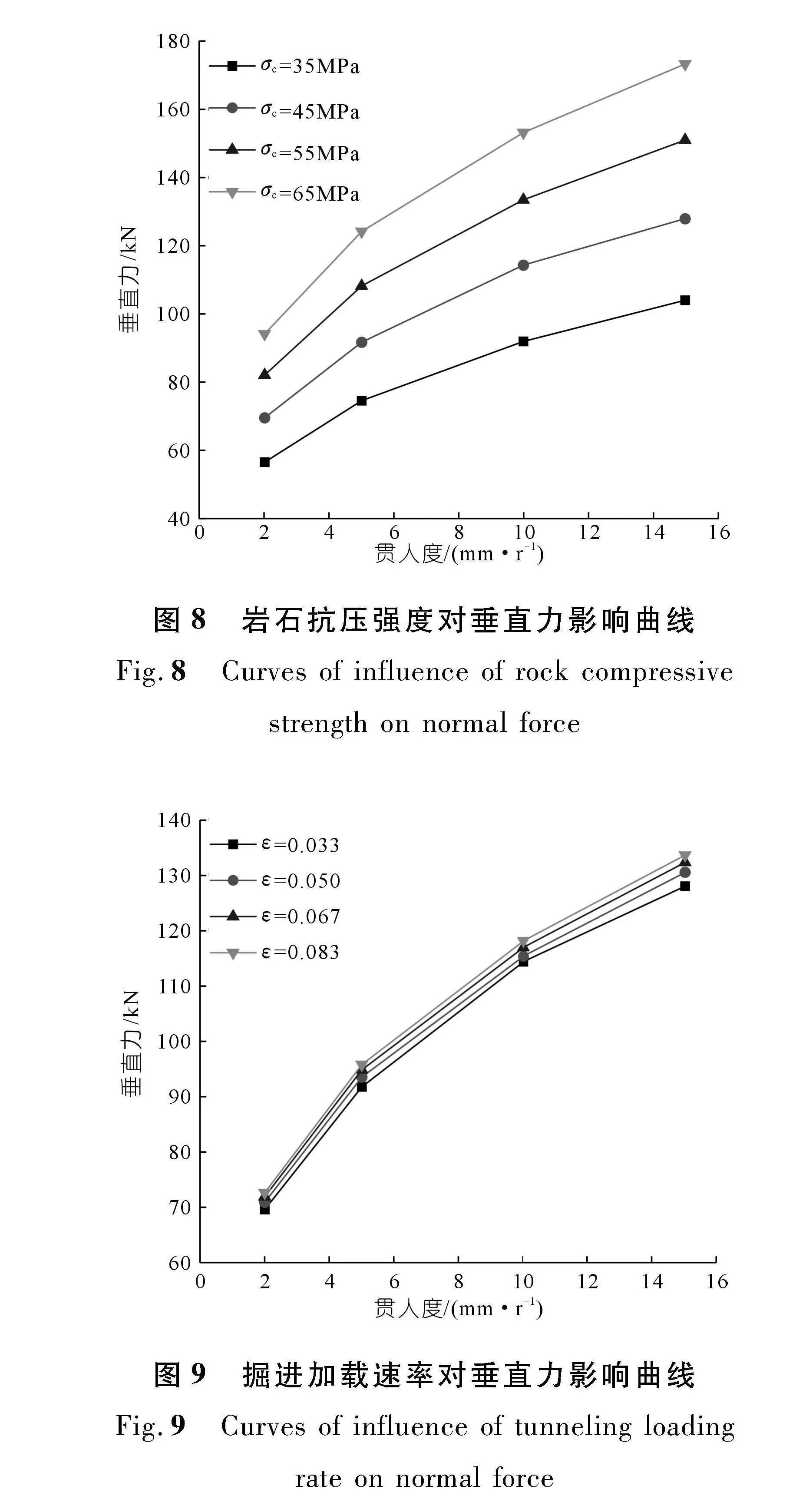
表4中前4个试验与仿真所用刀具皆为直径432 mm的17英寸盘形滚刀，抗压强度与本文近似。由图8可知，当贯入度分别为2 mm/r和5 mm/r时，本文仿真数据的计算结果分别为69.54 kN和91.69 kN，该计算结果与表4文献中试验结果相似，验证了本文仿真数据的可靠性。薛亚东等［22］对19英寸滚刀破岩进行了离散元模拟，在贯入度相似的情况下，抗压强度为105.6 MPa岩石对应的平均垂直力为239 kN，在量级上对本文有参考意义。

4.2" 影响因素分析

滚刀垂直力可以直接反映TBM刀盘推力的大小，且是实际工程中较多关注的参数。因此，通过改变仿真模型掘进参数和材料参数，选取滚刀破岩时岩石强度、掘进加载速率、刀刃宽度因素进行参数敏感性分析，计算不同工况下不同贯入度的滚刀垂直力。

4.2.1" 岩石抗压强度对垂直力的影响

取直径为432 mm，刀刃宽度为15 mm的17英寸常截面盘形滚刀，掘进加载速率0.033 r/s，滚刀的贯入度分别设置为2，5，10，15 mm/r；仅改变岩石材料中抗压强度参数，分别计算并绘制抗压强度35，45，55，65 MPa 4种情况下的滚刀垂直力变化曲线如图8所示。由图8可知，随着岩样抗压强度的增加，滚刀的垂直力也随之增加。实际工程中，TBM掘进往往采用“慢推慢磨”的方式，滚刀的贯入度控制在较低的范围内，因此17英寸的常截面盘形滚刀可以切削大部分中软硬岩。

4.2.2" 掘进加载速率对垂直力的影响

取直径为432 mm，刀刃宽度为15 mm的17英寸常截面盘形滚刀，抗压强度σc=45 MPa，滚刀的贯入度分别设置为2，5，10，15 mm/r，分别计算并绘制掘进加载速率0.033，0.05，0.067，0.083 r/s 4种情况下的滚刀垂直力变化曲线，分别对应刀盘转速为2～5 r/min，如图9所示。由图9可知，掘进加载速率对滚刀垂直力的影响较平和，且贯入度越小，影响越小。总体来说，垂直力随着掘进加载速率的提高而增大，但是不会存在急剧增长的情况。因此在实际工程中，如果遇到推力较大的情况，最主要的是要降低推进速度而减小贯入度，刀盘转速应保证在合理范围内不宜过低。

4.2.3" 刀刃宽度对垂直力的影响

为研究不同尺寸滚刀对垂直力的影响，取影响因素最大的几何参数刀刃宽度进行研究。改变模型中滚刀刀刃宽度，分别取值为15，20，25 mm，其与17～19英寸常截面盘形滚刀刀刃宽度值近似。抗压强度σc=45 MPa，掘进加载速率ε=0.033 r/s，滚刀的贯入度分别设置为2，5，10，15 mm/r；计算并绘制4种情况下的滚刀垂直力变化曲线，如图10所示。由图10可知，垂直力随着刀刃宽度的增大而增大，可见合理的刀具尺寸选择至关重要。在实际工程中应该预估滚刀承受的垂直力荷载，不应超过单刀的极限荷载承受值。

5" 结 论

（1） 通过LS-DYNA有限元软件建立滚刀破岩三维旋转切割模型，计算了常截面盘形滚刀破岩时的切削力，所得滚刀的切削力值与本文掘进试验和文献数据吻合较好，验证了仿真模拟的可靠性。

（2） 开展了滚刀破岩掘进试验，验证数值模拟结果。试验表明所测滚刀垂直力随时间变化曲线与数值模拟结果一致，呈波动特征，且滚刀切削力试验值与仿真数据误差较小。将本文仿真数据与CSM模型进行对比，发现整体结果较CSM模型值偏大，但更接近实验值。

（3） 通过改变数值模型中的岩石强度、掘进加载速率、刀刃宽度三大因素进行参数敏感性分析。研究得出在相同贯入度下，垂直力随上述影响因素的增大而提高，但掘进加载速率对垂直力的影响较小。后续可进行多因素正交敏感性参数研究，从更深层次剖析常截面滚刀的破岩受力规律。

参考文献：

［1］" 倪锦初，朱学贤，凌旋，等.香炉山深埋长隧洞TBM选型研究［J］.人民长江，2022，53（1）：154-159.

［2］" 王超，乔世范，刘红中.TBM破岩过程的滚刀受力计算模型研究［J］.工程力学，2021，38（10）：54-63.

［3］" TEALE R.The concept of specific energy in rock drilling［C］∥International Journal of Rock Mechanics and Mining Sciences amp; Geomechanics Abstracts.Pergamon，1965，2（1）：57-73.

［4］" ROXBOROUGH F F，PHILLIPS H R.Rock excavation by disc cutter［C］∥International Journal of Rock Mechanics and Mining Sciences amp; Geomechanics Abstracts.Pergamon，1975，12（12）：361-366.

［5］" 秋三藤三郞.デイスクカツタ一岩石破壞理论［J］.小松技術ミヤ一ナル，1970，16（3）：56-61.

［6］" ROSTAMI J.Development of a force estimation model for rock fragmentation with disc cutters through theoretical modeling and physical measurement of crushed zone［D］.Golden：Colorado School of Mines，1997：210-215.

［7］" LI X J，ZHANG Y Y，SUN X M.Numerical analysis for rock cutting force prediction in the tunnel boring process［J］.International Journal of Rock Mechanics and Mining Sciences，2021，144：104696.

［8］" SHE L，ZHANG S R，WANG C，et al.A cutting mechanics model of constant cross-section type disc cutter and its application based on dense core theory［J］.International Journal of Rock Mechanics and Mining Sciences，2022，150：105025.

［9］" 张桂菊，谭青，劳同炳.TBM盘形滚刀切削力学模型分析［J］.中南大学学报（自然科学版），2020，51（10）：2792-2799.

［10］张旭辉，夏毅敏，谭青，等.节理岩体下TBM单刃和双刃滚刀破岩特性研究［J］.哈尔滨工程大学学报，2016，37（10）：1424-1431.

［11］ZHANG Z X，WANG S F，HUANG X，et al.Application of block theory for evaluating face stability under disc cutters loading of TBM，case study of a water-conveyance tunnel project［J］.Tunnelling and Underground Space Technology，2019，90：249-263.

［12］耿麒，卢智勇，张泽宇，等.全断面隧道掘进机滚刀预切槽破岩数值模拟［J］.西安交通大学学报，2021，55（9）：9-19.

［13］李克金，张德文，李文，等.复合地层不同岩石强度下滚刀贯入试验研究［J］.现代隧道技术，2020，57（1）：148-155.

［14］韩伟锋.基于滚刀复合破岩物理实验的盾构刀间距设计［J］.科学技术与工程，2022，22（32）：14451-14457.

［15］CHO J，JEON S，YU S，et al.Optimum spacing of TBM disc cutters：a numerical simulation using the three dimensional dynamic fracturing method［J］.Tunnelling and Underground Space Technology，2010，25（3）：230-244.

［16］程永亮.TBM盘形滚刀破岩最优贯入度的数值模拟［J］.中南大学学报（自然科学版），2017，48（4）：936-943.

［17］耿麒，张俊杰，汪珂，等.基于FEM-SPH耦合的TBM滚刀切削仿真与试验研究［J］.山东大学学报（工学版），2022，52（1）：93-102.

［18］陈斌，罗夕容，曾首义.穿甲子弹侵彻陶瓷/钢靶板的数值模拟研究［J］.弹道学报，2009，21（1）：14-18.

［19］赵海雷，孙振川，张兵，等.基于CSM改进模型的TBM刀盘关键参数相关性研究［J］.隧道建设（中英文），2020，40（增1）：169-178.

［20］PAN Y，LIU Q，PENG X，et al.Full-scale rotary cutting test to study the influence of disc cutter installment radius on rock cutting forces［J］.Rock Mechanics and Rock Engineering，2018，51：2223-2236.

［21］XIA Y，GUO B，TAN Q，et al.Comparisons between experimental and semi-theoretical cutting forces of CCS disc cutters［J］.Rock Mechanics and Rock Engineering，2018，51：1583-1597.

［22］薛亚东，周杰，赵丰，等.基于MatDEM的TBM滚刀破岩机理研究［J］.岩土力学，2020，41（增1）：337-346.

（编辑：郑 毅）

Research on force of disc cutter during TBM rock breaking process

LI Zhongyan1，LIU Yang2，ZHANG Wenchao3，WU Zhiqiang1，LI Ruihong1

（1.School of Civil Engineering，Nantong Vocational University，Nantong 226007，China；

2.Suzhou High-Tech Zone High-speed Railway Construction Development Co.，Ltd.，Suzhou 215011，China；

3.School of Rail Transportation，Soochow University，Suzhou 215131，China）

Abstract：

Considering inadequacy of the traditional force models for commonly used constant-section disc cutters in engineering，a study was conducted to establish the rock-breaking force law for constant-section disc cutters to guide the design and construction of practical engineering projects.In this study，a three-dimensional rotational cutting model of disc cutters for rock breaking was developed using the finite element method to effectively simulate the rock-breaking process.By calculation，the cutting force of the constant-section disc cutter during rock breaking was obtained and compared with experimental and literature data.The results indicated a good agreement between the cutting force of the disc cutter and the actual situation，validating the reliability of the simulation.Rock-breaking excavation tests show that the measured normal force of the cutters varied with time，with fluctuating characteristics，which was consistent with the simulation results，at the same time the measured cutting force values deviated somewhat with simulated values.A comparison between the simulated values with the CSM model revealed that the overall results were slightly higher than those of the CSM model and closer to the experimental values.A parametric sensitivity analysis of the simulation model on rock strength，excavation loading rate，and blade width concluded that，under the same penetration depth，the normal force increased with the increase of the aforementioned factors，while the impact of the excavation loading rate on the normal force was relatively small.

Key words：

rock-breaking by disc cutter； cutting force； finite element； excavation test； CSM model