基于物理信息神经网络的长距离顶管施工顶力预测

摘要：

长距离顶管施工过程中，准确预测顶力是有效控制施工安全质量及进度的关键问题。基于知识数据融合的机器学习建模方法，将顶力计算物理模型与多层感知机相融合，构建了物理-数据双驱动的物理信息神经网络模型（PINN），用物理机制约束神经网络的训练机制，并引入改进的麻雀搜索算法（ISSA）对模型超参数取值进行优化，建立了ISSA-PINN顶管施工顶力预测模型；以河南省郑开同城东部供水工程顶管施工为例，选取524组工程实测数据验证了模型的有效性。计算结果表明：ISSA-PINN模型具有较高的预测精度，相较于单纯数据驱动模型，在测试集和新数据集中的预测性能分别提升了0.07和0.17，说明物理模型的融入对降低机器模型的过拟合风险和提高泛化能力有积极影响；相比于SSA和粒子群算法，ISSA算法寻优速度更快、适应度更好。研究结果可为顶管工程施工顶力控制提供参考。

关" 键" 词：

顶管施工； 顶力预测； 物理信息神经网络（PINN）； 改进麻雀搜索算法（ISSA）

中图法分类号： TV672+.2；TP181

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2025.01.020

收稿日期：2024-04-24；接受日期：2024-06-30

基金项目：

河南省学科创新引智基地项目“智慧水利”（GXJD004）；河南省水利厅科技攻关项目“长距离大直径复杂地层顶管施工关键技术研究及应用”（GG202358）

作者简介：

李" 博，男，高级工程师，主要从事水利工程管理工作。E-mail：41737923@qq.com

通信作者：

杨耀红，男，教授，博士，研究方向为工程管理、资源环境管理。E-mail：yangyaohong@ncwu.edu.cn

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2025） 01-0147-09

引用本文：

李博，刘宇翔，陈建国，等.基于物理信息神经网络的长距离顶管施工顶力预测

［J］.人民长江，2025，56（1）：147-155.

0" 引 言

随着城镇化建设的进一步发展，供水、供电等基础设施在地下空间建设使用的比例大幅增加，穿越公路、铁路、河流和地面建筑物是地下管道施工中常见的难题。顶管法作为非开挖的管道铺设方法，具有施工效率高、地面扰动较小、软土地层适应性强等特点，在地下空间建设中得到越来越多的应用［1］。

顶管工程中顶力是影响顶进设备选择、工作井布置及中继间设计的必要参数，也是施工过程中的关键控制参数。顶力过大时，顶进过程对环境的扰动显著，且管材破损风险提升；顶力过小则开挖面失稳，增加塌方与过度沉降风险［2］。因此，相关学者根据注浆过程的不同阶段［3］、顶管顶进过程中土体拱形效应和泥浆状态［4］、管土浆的不同接触状态［5］，以及针对大断面矩形顶管摩阻力计算［6］、钢管顶管与砂土摩阻力计算［7］等特殊顶管施工情景，构建了相应的物理模型展开顶力计算。在岩石顶管施工中，触变泥浆通过其支撑作用实现减阻效果，钟祖良［8］、邓志云［9］、Peng［10］等学者根据泥浆在管材与岩石间是否形成完整泥浆套，将管-岩接触划分成不同的接触状态，提出岩石顶管的顶力计算模型。以上计算方法对于短距离顶管施工的顶力计算准确度尚可，但应用于长距离顶管工程则会出现较大的累计误差［11］。

近年来，人工智能（AI）方法在岩土工程领域的应用日益广泛，尤其是在处理工程施工参数的数据随机性、不确定性和非线性方面，优势更显著［12］。目前已有相关研究将基于机器学习的人工智能方法应用于顶管施工的不同方面，例如：基于正则化极限学习机（RELM）预测网接收基坑周围地面沉降［13］、使用BP神经网络预测矩形顶管地表沉降［14］、基于PSO-SVR模型的施工参数预测［15］、基于GRU深度学习框架的顶管运动轨迹多步提前预测［16］、使用图卷积神经网络堆叠门控循环单元预测水下弯曲顶管顶力［17］等。这些研究在监测数据集上表现出了良好的预测性能。但在现有研究中，多数机器学习方法主要依赖数据驱动策略，导致模型在应用过程中难以应对数据规模小、数据质量不高、可解释性不强等问题。知识驱动模型通常能构建相对明确的因果关系，普适性优于数据驱动模型，但在数据非线性、不确定性等背景下，知识驱动模型建模过程中会遇到显著的困难［18］。图1揭示了当前数据驱动建模、知识驱动建模和模型机理揭示效果的基本相关关系。为达到理想的机理揭示效果，知识驱动模型要求具备全面的领域知识作为支撑，机器学习模型依赖于大规模高质量的数据保障。目前，绝大多数研究均处于拥有部分知识和部分数据的交织状态，如何将这两种信息资源有效融合以优化建模效果，已成为一个备受瞩目的新兴研究方向。

将物理信息、先验知识、专家知识融入机器学习模型之中，能有效提升模型结果的可解释性，并使结果更贴近理论预期［19-20］。目前，知识嵌入型机器学习模型已在图像识别［21］、湖泊温度预测［22］、合金配比优化［23］、 TBM推力扭矩预测［24］等领域展现出广泛的应用价值。尤其是Raissi等［25］提出了物理信息神经网络（PINN），可以把研究对象内在的物理规律和实测数据融合集成，实现知识和数据的双驱动，并成功应用于非稳态温度场和未知热源预测［26］、Burgers-Fisher方程求解［27］、复合地层隧道掘进地表沉降预测［28］、结构振动分析［29］等领域，但在实际工程建设中的应用还明显不足。

顶管施工中顶力是克服摩阻力实现顶进的原动力，并且受到地层、减阻工程措施等多种因素的影响，有其内在的物理机制。

本文拟将顶管施工顶力物理模型融入到多层感知机（MLP）模型中，构建物理-数据双驱动的PINN预测模型，并引入改进的麻雀搜索算法（ISSA）对模型超参数取值进行优化，形成预测顶管施工顶力的ISSA-PINN模型；然后将模型用于河南省郑开同城东部供水工程进行验证，并进行计算对比分析，验证ISSA-PINN模型的有效性，以为合理准确预测顶管施工顶力提供一种新的途径。

1" ISSA-PINN融合模型构建

1.1" 顶力计算物理模型

顶管施工中通常将管土摩阻力和顶管机正面压力之和作为顶进施工总顶力，顶力计算需考虑管-土-泥浆套三者的耦合作用。王双等［30］在深入探讨施工过程中管土接触状态对减阻效果影响的基础上，利用管体顶进运动过程中泥浆的剪应力代替传统管土摩阻力，构建了软岩地质条件下圆形顶管顶力物理计算模型。由于该物理模型是较新的顶力计算模型，考虑影响因素比较全面，尤其是其计算条件与本文案例工程施工状况相符，因此本文直接采用该顶力计算物理模型。在管体自重、泥浆浮力、注浆量及超挖量等因素作用下，常见的接触类型有管体下沉、管体悬浮、管体上浮此3类，如图2所示。

基于以上对泥浆套状态的分析可知，顶进施工过程中摩阻力由管体与泥浆之间剪应力与管壁土体摩擦力两部分组成，其中管体与泥浆之间剪应力计算可由常压条件下幂律模型构建，顶力计算公式为

FJ=F+FN（1）

F=Kvhna+b2tanφ2/［2.562rr0/（r-r0）］·［（1-μ2）/E+（1-μ20）/E0］+c′L管体上浮或下沉2πr0KvhnL管体悬浮（2）

FN=γmHπ4D2（3）

W=2πγcr0t0（4）

F′=πρ0gr20（5）

式中：FJ为顶力，kN；F为摩阻力，kN；FN为顶管机正面压力，kN；W为管体自重，kN/m；F′为泥浆提供浮力，kN/m；K为流体稠度系数，Pa·s1/2；v为平均顶进速度，mm/min；h为施工空隙，m；n为流型参数；r0为混凝土管半径，m；r为顶管机半径，m；μ为土体泊松比；E为土体弹性模量，MPa；μ0为混凝土管泊松比；E0为混凝土管弹性模量，MPa；φ为土壤内摩擦角；c′为管土黏聚力，取0.2～0.7 kPa；a为管体与泥浆接触宽度，m；b为管体与土体接触宽度，m；L为顶进施工距离，m；γm为覆土平均重度，kN/m3；H为覆土厚度，m；D为管材直径，m；γc为混凝土重度，kN/m3；t0为混凝土管厚度，m；ρ0为泥浆密度，g/cm3；g为重力加速度，m/s2。

1.2" 神经网络模型

多层感知机（MLP）是一种应用广泛的人工神经网络模型，它在解决复杂非线性建模问题中表现出强大的鲁棒性，网络结构由一个输入层、一个输出层和多个隐藏层构成，借助多个隐藏层的神经元来实现模型输入与输出的复杂映射［31］。MLP模型通过反向传播的学习过程自动调整权重和偏置，从而逐渐改善模型的预测能力。其中隐藏层的输出可表示为

Z（l）=σ（l）（w（l）x+b（l））（6）

式中：l为隐含层序号；x为输入向量，在本文中指现场采集的施工数据；Z为第l层输出；w为第l层的权重矩阵；b为第l层的偏置向量；σ为第l层的激活函数，本文采用ReLU函数。MLP网络反向传播、损失函数计算、权重矩阵以及偏置项的更新可表示为

LossMSE=1nni=1（y^i-yi）2（7）

w2=w1-η·Lossω（8）

b2=b1-η·Lossb（9）

式中：i为样本编号；n为样本数量；yi、y^i分别为第i个样本的真实值、预测值；η为学习率。对于每个权重w和偏置向量b，使用梯度下降法更新。

1.3" ISSA-PINN融合模型

数据驱动的神经网络方法依赖于现有数据集完成训练学习，其模型可解释性不强，且存在训练学习结果过拟合的风险。顶管施工顶力计算物理模型，从线性模型角度描述顶力随顶进距离增加的渐进增长过程，但也存在累计误差较大、普适性不强等局限性。将物理模型与机器学习方法融合，用物理机制约束神经网络的训练机制，可以发挥机器学习建模方法的优势，同时将物理模型作为正则项加入神经网络的损失函数中，降低网络过拟合的风险。物理模型（公式（1））可表示为

FJ=f（l）（10）

将物理模型计算值与预测值的均方误差以加权的方式结合网络自身的损失函数，形成神经网络的总损失函数，如公式（11）～（12），实现物理模型的融入，进而构建PINN模型，模型网络结构如图3所示。

Lossk=1nni=1［f（li）-yi］2（11）

Loss=w1LossMSE+（1-w1）Lossk（12）

为确定PINN模型超参数以及融合模型权重w1取值，本文采用改进的麻雀搜索算法（improved sparrow search algorithm）进行优化。麻雀搜索算法是通过模仿麻雀的觅食和反捕食行为，来模拟局部和全局的搜索寻优［32］。在麻雀搜索算法中，麻雀种群被划分为发现者、加入者和侦察者3种角色，各角色遵循其特定的更新规则完成寻优过程［33］。本次研究将PINN模型预测结果的均方误差设置为搜索过程中的适应度函数，即：

fitness=w11nni=1（y^i-yi）2+（1-w1）×1nni=1［f（li）-yi］2（13）

麻雀搜索算法相较于其他群体智能算法具有收敛速度快、稳定性强、全局搜索能力强的优点，但随着迭代次数的增加，容易陷入局部最优。因此本文将初始种群改进和迭代策略改进相结合来改进麻雀搜索算法：

（1） Tent混沌映射。

随机生成的麻雀种群均匀性不强、多样性较差，对初始种群进行混沌映射操作可以有效改善初始种群的性能，其中Tent混沌映射具有出色的优化性能［34］。Tent混沌映射数学表示为

Mk+1=2Mk""" 0≤Mk≤0.52（1-Mk）" 0.5＜Mk≤1（14）

式中：Mk为第k次迭代时的映射函数值。

（2） Levy飞行策略。

Levy飞行策略是一种随机行为策略，其本质是一种非高斯随机步态，步长服从概率分布，其飞行特点为长时间进行小步长随机游走，偶尔出现大步长游走［35］。为了降低种群陷入局部最优的风险同时保持求解精度和能力，本文将Levy飞行策略引入侦察者反捕食行为的位置更新策略中。其数学表达式为

Xi，j（t+1）=Levy（d）·Xbest（t）+β·Xi，j（t）-" Levy（d）·Xbest（t）figt;fgXbest（t）+K·Xi，j（t）-Xworst（t）fi-fw+e" fi=fg（15）

Levy（d）=0.01·r1·σr21/β（16）

σ=Γ（1+θ）·sin（θπ/2）Γ［（1+θ）/2］·θ·2（θ-1）/21/θ（17）

式中：Xbest（t）为当前全局最优位置；Xworst（t）为当前全局最差位置；β为步长控制参数，服从均值为0、方差为1的正态分布随机数；K表示麻雀运动方向，是-1～1之间的随机数；fi，fg，fw分别为当前麻雀的适应度值、全局最优值和全局最差值；e为一个常数，以防止分母为零；Γ为伽马函数；θ为常数，常取1.5；r1，r2为0～1之间的随机数。

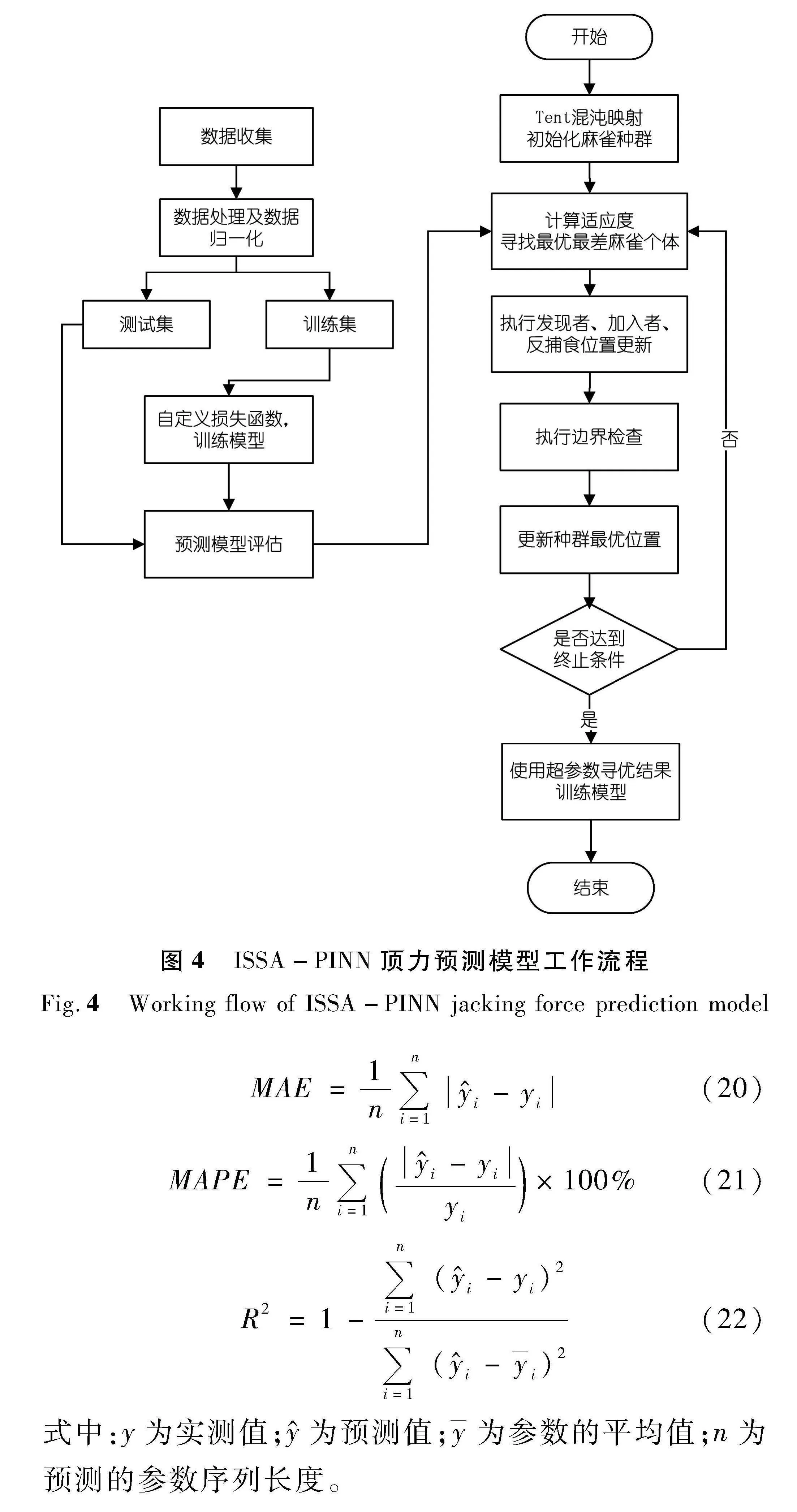
ISSA-PINN顶力预测模型工作流程如图4所示。

1.4" 模型评估指标

选用均方误差（MSE）、均方根误差（RMSE）、平均绝对误差（MAE）、平均相对误差（MAPE）、决定系数（R2）5个指标评估模型预测精度。具体的计算公式为

MSE=1nni=1（y^i-yi）2（18）

RMSE=1nni=1（y^i-yi）2（19）

MAE=1nni=1y^i-yi（20）

MAPE=1nni=1y^i-yiyi×100%（21）

R2=1-ni=1（y^i-yi）2ni=1（y^i-y—i）2（22）

式中：y为实测值；y^为预测值；y—为参数的平均值；n为预测的参数序列长度。

2" 实例分析

2.1" 工程概况

河南省郑开同城东部供水工程输水管道总长度108.01 km，共采用顶管型式穿越施工141处，总长约38 km，其中最长顶管约1.1 km。结合工程土层的物理特性及地下水等因素，选用泥水平衡顶管施工。顶管穿越施工十三大街段工程区地处黄淮冲积平原北部，地面高程约为74.6～77.9 m，岩性主要为粉砂、细砂、砂壤土和粉质壤土，地质结构主要为黏砂多层结构。地下水埋深4.1～10.5 m，水位66.85～70.70 m。

本文模型训练验证使用的数据集，由2号和12号工作井段（图5）现场收集。2号工作井至2号接收井段管材直径3 300 mm，平均覆土深度5.6 m，工作井管中心线高程67.6 m，接收井管中心线高程67.6 m，顶进长度629 m，坡降为平坡，地层类型为轻粉质壤土；12号工作井至12号接收井段管材直径3 300 mm，平均覆土深度9.08 m，工作井管中心线高程67.239 m，接受井管中心线高程67.621 m，顶进长度151 m，坡降-0.252%，地层类型为中粉质壤土。

2.2" 数据获取及预处理

顶管工程施工参数取值如下：H=5.60 m，r0=1.65 m，r=1.68 m，v=75 mm/min，b=0.28 m，a=10.09 m，h=0.03 m。混凝土管段参数如下：E0=3.35×104 MPa，μ0=0.2，γc=26.0 kN/m3，t0=0.25 m。泥浆材料参数如下：ρ0=1.05 g/cm3，n=0.5，K=1.31 Pa·s1/2。土层参数取各层土平均值：E=7.4 MPa，μ=0.35，c=11.2 kPa，φ=10.9°，γm=17.4 kN/m3，c′=0.2 kPa；g=9.8 m/s2。经计算，该工程W=67.39 kN/m，F′=89.81 kN/m，说明在注浆量充足的情况下，管段施工过程中在泥浆套中呈现上浮形态的概率较大，则顶力物理模型计算公式为

FJ=21.095L+833.403（23）

在顶进施工过程中，顶管机操作平台会记录刀盘电流、刀盘转速、排泥压力、前舱压力、顶进速度和顶进距离6项施工参数。将已完成施工的2号工作井和12号工作井监测数据输入模型，进行顶力预测的训练和验证。由于在施工过程中数据的采集会受到人为操作、传感器、传输设备等因素的影响，因此施工参数数据集中不可避免存在异常值或缺失值，故在数据的预处理中，采用箱线图检测法对数据集进行检测，删除异常值和缺失值。

2.3" 模型预测结果

经过数据预处理，2号工作井段共得到335组施工数据，12号工作井段共得到189组施工数据。使用2号工作井段的施工数据作为模型的训练数据，并随机选取其中268组数据作为训练集、67组数据为验证集；选取12号工作井段189组施工数据作为额外验证集进一步评估模型的泛化能力。本文实验是在Python 3.8环境下进行的。

2.3.1" MLP模型与其他机器学习模型对比分析

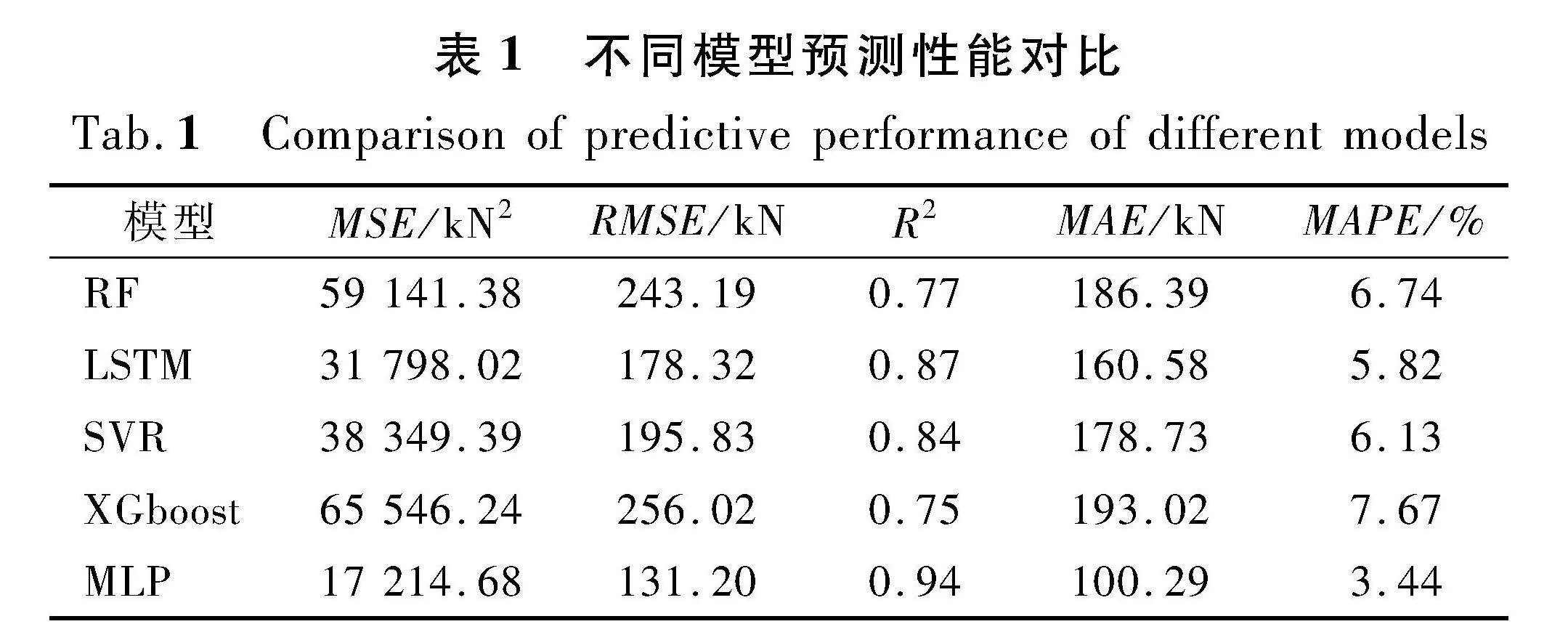
将MLP模型与当前研究中较常应用的随机森林（RF）模型［36］、长短期记忆网络（LSTM）模型［37］、支持向量回归（SVR）模型［15］、极致梯度提升树（XGboost）模型进行对比分析。统一使用2号工作井数据集进行训练和预测，并使用ISSA对模型的超参数进行优化设置。训练集结果如表1所列，结果表明，MLP模型在5项评估指标的表现上均优于其他几种机器学习模型，同时模型预测结果在令人满意的范围内，说明MLP模型在非线性建模方面的特点十分契合顶力预测问题。因此，本文选用MLP模型作为融合模型的基础模型。

2.3.2" 改进麻雀搜索算法对PINN优化效果分析

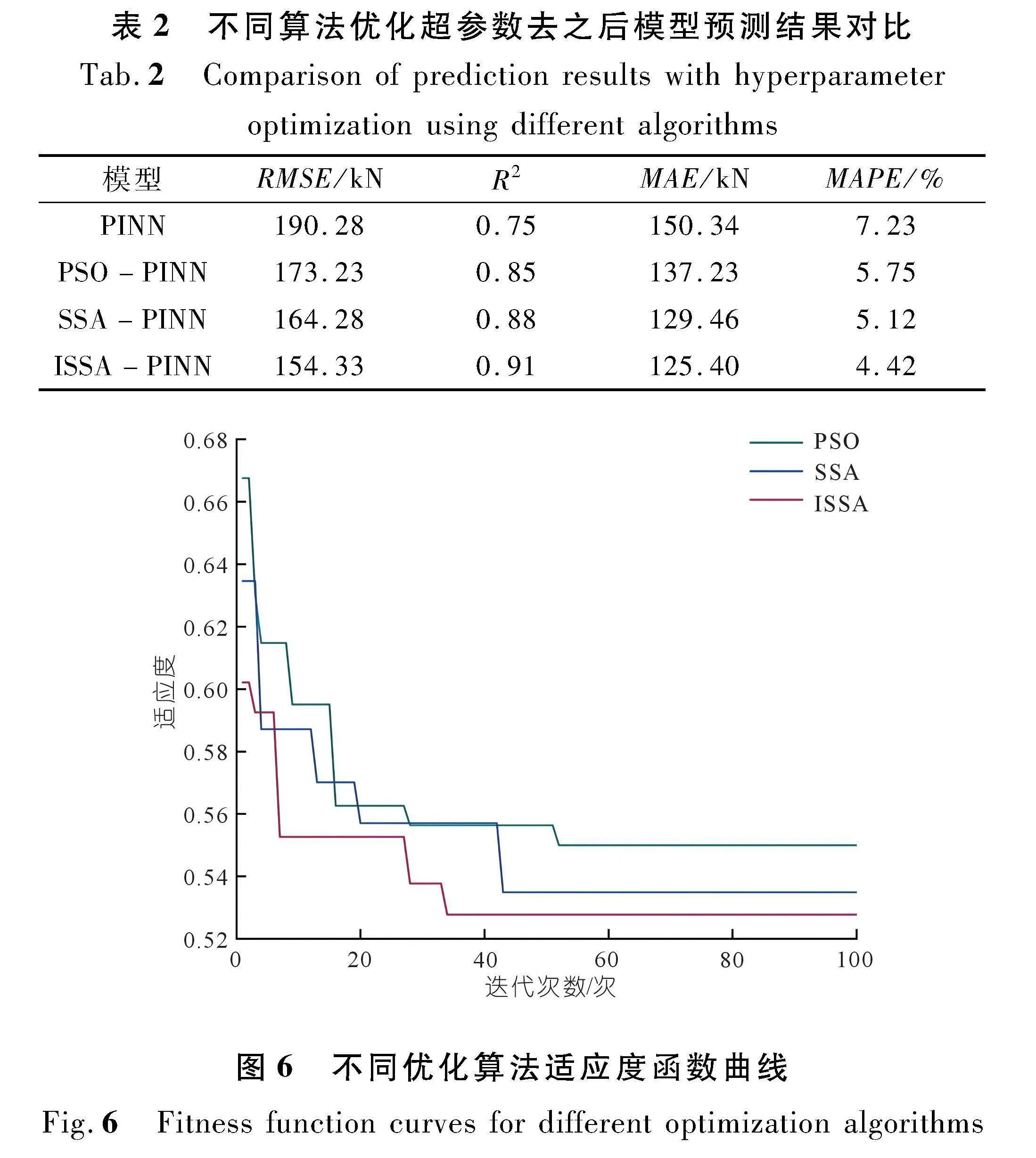
将ISSA-PINN模型、SSA-PINN模型、粒子群算法（PSO）优化的PINN模型和未进行超参数寻优的PINN模型分别进行寻优和训练，计算各个模型预测结果的均方根误差（RMSE）、平均绝对误差（MAE）、 平均相对误差（MAPE）、决定系数（R2）来评估预测性能，结果如表2所列。结果表明，ISSA-PINN模型预测的各项指标均优于未进行超参数寻优的PINN模型和SSA-PINN、PSO-PINN模型。进一步比较分析ISSA算法与未进行改进的SSA算法、PSO算法的寻优性能，分别使用3种算法对PINN模型进行超参数寻优，并记录适应度函数随迭代次数的变化，变化曲线如图6所示。由图6可知，相较于SSA算法和PSO算法，ISSA算法在寻优初始阶段有适应度更优的初始解，且在寻优过程中曲线下降速度更快，寻优结果适应度最小，说明使用Tent混沌映射和Levy飞行策略对SSA算法产生了积极的改进效果，ISSA算法比SSA、PSO算法有更快的收敛速度和更强的全局搜索能力。

因此，采用ISSA算法寻优确定的最优参数组合作为模型的最终参数：epoch为86，batch-size为16，w1为0.89，隐藏层神经元数为34。

2.3.3" ISSA-PINN融合模型效果分析

为了验证物理模型的融入对机器学习模型的积极影响，训练具有相同结构和超参数的ISSA-MLP模型和ISSA-PINN模型，对同一目标进行预测输出。将模型应用于相同现场数据样本中，通过计算两种模型输出结果与现场记录值的误差来确定物理模型对MLP模型的影响，结果如图7～12和表3所示。

如图7所示，训练集上ISSA-MLP模型和ISSA-PINN模型的预测值都呈现出较高的预测精度。但在单一样本视角下，从图8可以看出ISSA-PINN模型预测值存在高于ISSA-MLP预测模型和现场记录值的情况，在某些样本中ISSA-MLP模型预测值与现场记录值几乎重合，这是因为ISSA-PINN模型中物理模型的融入。计算顶力的物理模型已经尽可能反映顶进施工的物理机理，但其中尚有不能完全用物理模型描述的物理机制，为确保计算结果能指导整个施工过程正常安全进行，常采用偏保守的假设处理，导致物理模型的计算值较高，进而在融入机器学习模型的过程中影响机器学习模型的输出。尤其对于长距离顶管情况，距离越长，物理模型计算偏差越大。

由表3可知，单纯由数据驱动的ISSA-MLP模型在训练集的学习上表现出了更好的误差表现，ISSA-PINN模型预测结果的5个评估指标都略低于ISSA-MLP模型的预测结果，但总体处于一个令人满意的预测精度水平。

测试集的预测结果可以直观呈现出模型的泛化能力。从图9可以看出，ISSA-MLP模型和ISSA-PINN模型都在很大程度上与记录值具有相似的趋势；从表3模型评估指标可直观发现ISSA-PINN模型在测试集的预测精度高于ISSA-MLP模型。测试集中，使用ISSA-MLP模型预测顶力时，MSE和MAPE出现大幅度增加，说明ISSA-MLP模型在训练集上可能存在过拟合，导致模型在测试集的泛化能力不强。

图10中测试集预测值与记录值的绝对百分比误差指标显示，在测试集样本中存在编码24，33，37等误差较大的几组样本。虽然在顶进施工过程中存在顶力随顶进距离增加而增加的趋势，但其变化机理是耦合土层不确定性、注浆效果稳定性、顶管操作手参数调整等多方面的复杂非线性过程。这几个方面的因素出现变化，顶力的记录值可能随之产生相应的增量。此时单纯数据驱动的ISSA-MLP模型在面对此类数据时，会因为训练数据信息有限而产生较大的误差，但由于物理模型的融入，ISSA-PINN模型在预测这些大误差样本时，结果出现了精度的提升，这也说明了物理模型融入对提升泛化能力的积极作用。

选用不参与模型训练的12号工作井段记录数据作为新数据集进行预测，可以进一步反映出模型的泛化能力。从图11可以看出，单纯数据驱动的ISSA-MLP模型在多个样本点出现了较大误差的预测结果，且在这些样本点，ISSA-MLP模型预测值显著低于记录值，说明虽然处于相似的施工背景下，单纯的数据驱动模型并不能很好地将学习的信息进行普适性的“迁移”。融合物理模型的ISSA-PINN模型在新的数据集上基本反映出顶力的变化趋势，且ISSA-PINN模型的顶力预测值大多维持在一个保守的水平，面对顶力激增和骤降的数据样本，ISSA-PINN模型能够输出合理的顶力预测值。从指导施工过程的角度来看，这样的结果无疑是非常有利的。

由图12可知，ISSA-PINN模型在新的数据集上其预测结果精度明显高于ISSA-MLP模型。尽管相较于2号工作井段数据集，预测结果出现误差增大的情况，但与ISSA-MLP模型相比，ISSA-PINN模型的泛化能力表现更强。

3" 结论与展望

针对顶管施工中顶力的预测控制问题，本文把物理模型和机器学习模型相融合，用物理机制约束神经网络的训练机制，并引入改进的麻雀搜索算法对模型超参数取值进行优化，构建了针对顶管施工顶力预测的ISSA-PINN模型，结合实际工程对顶力的融合预测模型进行训练、验证和评估，并把单纯数据驱动模型和融合模型预测结果做对比分析，得到如下结论：

（1） 构建物理-数据双驱动的 PINN 融合顶管施工顶力预测模型，并采用基于Tent混沌映射和Levy飞行策略改进的麻雀搜索算法（ISSA）对融合模型的超参数进行优化，形成ISSA-PINN融合顶力预测模型，可以实现顶管施工顶力的高精度预测。

（2） 将物理模型融入MLP模型中构建ISSA-PINN融合模型，与单纯数据驱动的ISSA-MLP模型相比，ISSA-PINN模型在同工程段验证集和新工程段验证数据集中都有更高的预测精度和更强的泛化能力，ISSA-PINN模型的预测结果决定系数分别提高了0.07和0.17，说明物理模型的融入对机器学习模型在减少过拟合风险和提高泛化能力方面的影响是积极的。

当然，由于顶管施工过程的复杂性，物理-数据双驱动的PINN模型尚需进一步完善。一方面，物理模型对物理机理的表达、物理模型与数据模型的有机融合方法尚待进一步深入研究；另一方面，使用单一工程数据训练的机器学习模型能否有效地应用于存在差异的类似工程，如何利用相似工程“大数据”深化模型训练，提高模型的普适性，用于指导新的工程建设，也是有意义的研究课题。

参考文献：

［1］" 张波，刘晶晶.顶管法下穿既有轨道交通隧道安全性研究［J］.中国安全生产科学技术，2023，19（增1）：162-167.

［2］" LI P N，DAI Z Y，HUANG D C，et al.Impact analysis for safety prevention and control of special-shaped shield construction closely crossing multiple operational metro tunnels in shallow overburden［J］.Geotechnical and Geological Engineering，2021，40（4）：1-18.

［3］" 侯俊锋，肖楚怀，李江，等.考虑管-土-浆相互作用的管段施工过程力学模型［J］.地下空间与工程学报，2023，19（3）：767-776.

［4］" ROBERT D B.Jacking loads and ground deformations associated with microtunneling［D］.Illinois：University of Illinois at Urbana-Champaign，1998.

［5］" KONG C，GUAN G Q，GU S，et al.Frictional resistance calculation and jacking force prediction of rectangular pipe jacking［J］.Scientific Reports，2023，13（1）：14992.

［6］" 甘淑清，彭立敏，雷明锋，等.考虑管-土/泥浆接触状态的浅埋大断面矩形顶管隧道摩阻力计算方法研究［J］.中南大学学报（自然科学版），2023，54（3）：1178-1186.

［7］" MEI Z，XIAO A F，MEI J H，et al.Experimental study on interface frictional characteristics between sand and steel pipe jacking［J］.Applied Sciences，2023，13（3）：2016-2042.

［8］" 钟祖良，刁小军，刘新荣.长距离深埋岩石地层顶管摩阻力计算方法研究［J］.岩土工程学报，2022，44（11）：2063-2070.

［9］" 邓志云，刘新荣，钟祖良，等.长距离岩石顶管工程管节摩阻力研究［J］.地下空间与工程学报，2023，19（3）：750-759.

［10］PENG C，LIU X R，DENG Z Y，et al.Study on the pipe friction resistance in long-distance rock pipe jacking engineering［J］.Underground Space，2023（9）：173-185.

［11］PEERUN M I，ONG D E L，DESHA C.Strategic review on enhanced DEM simulation and advanced 3D particle printing techniques to improve pipe-jacking force prediction［J］.Tunnelling and Underground Space，2022，123（5）：104415.

［12］ZHANG W G，LI H R，LI Y Q，et al.Application of deep learning algorithms in geotechnical engineering：a short critical review［J］.Artificial Intelligence Review，2021，54（8）：1-41.

［13］HAN Y L，WANG Y，LIU C Y，et al.Application of regularized ELM optimized by sine algorithm in prediction of ground settlement around foundation pit［J］.Environmental Earth Sciences，2022，81（16）：413-428.

［14］HU D，HU Y J，YI S，et al.Surface settlement prediction of rectangular pipe-jacking tunnel based on the machine-learning algorithm［J］.Journal of Pipeline Systems Engineering and Practice，2024，15（1）：04023061.

［15］ZHOU H，HUANG S，ZHANG P，et al.Prediction of jacking force using PSO-BPNN and PSO-SVR algorithm in curved pipe roof［J］.Tunnelling and Underground Space，2023，138（1）：105159.

［16］YANG Y F，LIAO S M，LIU M B.Dynamic prediction of moving trajectory in pipe jacking：GRU-based deep learning framework［J］.Frontiers of Structural and Civil Engineering，2023，17（7）：994-1010.

［17］DAI Z Y，LI P N，LIU J，et al.Data-driven prediction for curved pipe jacking performance during underwater excavation of ancient shipwreck using an attention-based graph convolutional network approach［J］.Expert Systems with Applications，2024，236（2）：121393.

［18］乔骥，赵紫璇，王晓辉，等.面向电力系统智能分析的机器学习可解释性方法研究（二）：电网稳定分析的物理内嵌式机器学习［J］.中国电机工程学报，2023，43（23）：9046-9059.

［19］FARZAM F，SALAHUDDIN M H，BRAHIM H，et al.Knowledge-embedded machine learning and its applications in smart manufacturing［J］.Journal of Intelligent Manufacturing，2022，34（7）：2889-2906.

［20］LAURAV R，SEBASTIAN M，KATHARINA B，et al.Informed machine learning-a taxonomy and survey of integrating prior knowledge into learning systems［J］.IEEE Transactions on Knowledge and Data Engineering，2021，35（1）：614-633.

［21］ALEXK，ILYA S，GEOFFREY E H.ImageNet classification with deep convolutional neural networks［J］.Communications of the ACM，2017，60（6）：84-90.

［22］JIA X W，WILLARD J，KARPATNE A，et al.Physics guided RNNs for modeling dynamical systems：a case study in simulating lake temperature profiles［C］∥Proceedings of the 2019 SIAM International Conference on Data Mining，Bangkok，2019：558-566.

［23］苗海宾，向朝建，刘胜楠，等.专家知识增强的机器学习建模在高强高导铜合金开发中的应用［J］.工程科学学报，2023，45（11）：1908-1917.

［24］LIU B，WANG J W，WANG R R，et al.Intelligent decision-making method of TBM operating parameters based on multiple constraints and objective optimization［J］.Journal of Rock Mechanics and Geotechnical Engineering，2023，15（11）：2842-2856.

［25］RAISSI M，PERDIKARIS P，KARNIADAKIS E G.Physics-informedneural networks：a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations［J］.Journal of Computational Physics，2019，378（1）：686-707.

［26］余波，甘子玉，张森林，等.基于物理信息神经网络预测2D/3D非稳态温度场及热源［J/OL］.工程力学：1-13（2023-10-17）［2024-04-10］.http：∥kns.cnki.net/kcms/detail/11.2595.O3.20231013.1641.006.html.

［27］徐健，朱海龙，朱江乐，等.基于物理信息神经网络的Burgers-Fisher方程求解方法［J］.浙江大学学报（工学版），2023，57（11）：2160-2169.

［28］潘秋景，吴洪涛，张子龙，等.基于多域物理信息神经网络的复合地层隧道掘进地表沉降预测［J］.岩土力学，2024，45（2）：539-551.

［29］CHEN Z L，LAI S K，YANG Z C.AT-PINN：advanced time-marching physics-informed neural network for structural vibration analysis［J］.Thin-Walled Structures，2024，196（3）：111423.

［30］王双，夏才初，葛金科.考虑泥浆套不同形态的顶管管壁摩阻力计算公式［J］.岩土力学，2014，35（1）：159-166，174.

［31］ZHANG Y，CHEN G P，MALIK O P，An artificial neural network based adaptive power system stabilizer［J］.IEEE Transactions on Energy Conversion，1993，8（1）：71-77.

［32］XUE J K，BO S.A novel swarm intelligence optimization approach：sparrow search algorithm［J］.Systems Science Control Engineering，2020，8（1）：22-34.

［33］尹德鑫，张达敏，蔡朋宸，等.改进的麻雀搜索优化算法及其应用［J］.计算机工程与科学，2022，44（10）：1844-1851.

［34］张娜，赵泽丹，包晓安，等.基于改进的Tent混沌万有引力搜索算法［J］.控制与决策，2020，35（4）：893-900.

［35］IACCA G，SANTOSJUNIOR D V C，MELO D V V.An improved Jaya optimization algorithm with Levy flight［J］.Expert Systems with Applications，2021，165（3）：113902.

［36］张晟斌，舒恒，刘夏临，等.基于机器学习的水平定向钻钻孔围岩智能分类探讨［J］.人民长江，2023，54（12）：156-165.

［37］王晓玲，李克，张宗亮，等.耦合ALO-LSTM和特征注意力机制的土石坝渗压预测模型［J］.水利学报，2022，53（4）：403-412.

（编辑：胡旭东）

Jacking force prediction of long-distance pipe jacking construction based on physical information neural network

LI Bo1，LIU Yuxiang2，CHEN Jianguo1，YANG Yaohong2，3，ZHANG Zhe2

（1.Henan Water Conservancy Engineering First Group Co.，Ltd.，Zhengzhou 450000，China；

2.School of Water Conservancy，North China University of Water Resources and Electric Power，Zhengzhou 450046，China；

3.Henan Provincial Key Laboratory of Hydrosphere and Watershed Water Security，Zhengzhou 450046，China）

Abstract：

Accurately predicting the jacking force is a crucial for effectively controlling the safety，quality，and schedule of the long-distance pipe jacking project.In this paper，based on the machine learning modeling method of knowledge data fusion，the jacking force calculation physical model was combined with the multi-later perceptron to construct a physics-informed neural network model （PINN） driven by physics and data，the physical mechanism was used to constrain the training mechanism of the neural network，and the improved sparrow search algorithm was introduced to optimize the hyperparameter value of the model.Therefore，the ISSA-PINN jacking force prediction model was established.Taking the water supply project for Zhengzhou-Kaifeng City demonstration area as an example，524 sets of actual measurement data were selected to validate the model's effectiveness.The results showed that，compared to data-driven models，the ISSA-PINN model achieves high prediction accuracy with 0.07 and 0.17 improvement on test datasets and new datasets respectively.This demonstrated that incorporating physical models have positive effects to reducing over fitting and enhancing generalization of MLP model.The ISSA algorithm demonstrated faster optimization speed and better fitness compared to the standard Sparrow Search Algorithm （SSA） and Particle Swarm Optimization （PSO）.The research results can provide reference for jacking force control in pipe jacking engineering construction.

Key words：

pipe jacking construction； jacking force prediction； physics-informed neural network model （PINN）； physical-data dual drive；

improved sparrow search algorithm