水库泄流洪水波在宜昌—大通河段传播规律研究

摘要：

在当前水利工程和防洪管理中，水库泄流洪水波传播问题备受关注。以长江宜昌—大通干流河段为例，构建了一维水动力学模型，模拟了不同工况条件下洪水波的传播特性，并对比分析了沿程洪水演进规律。研究结果表明：① 断波洪水的形成可在不同程度上缩短下游河段的峰现时间，随着断波流量的增加，以运动波传播的河段距离明显缩短，洪水波形变指数增加；② 随着洪峰流量持续时间的延长，同样会缩短以运动波特性传播的洪水波演进的距离，并增加洪水波形变指数，但同一站点或是里程上的峰现时间会有推后，洪峰历时延长；③ 多波束断波条件下，计算波速普遍较高，随着沿程距离的增加波形变指数递减，但多波束传播条件下形变指数沿程衰减过程明显放缓；④ 当有支流入汇时，沿程站点洪峰流量变化均表现出明显的非一致性，高流量历时明显延长。研究成果对于揭示水库泄流洪水波传播规律具有重要意义，可为区域防洪管理提供参考。

关" 键" 词：

水库泄流； 洪水波； 传播特性； 形变指数； 水动力学模型； 长江

中图法分类号： P332.2

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2025.01.004

收稿日期：2024-07-24；接受日期：2024-09-11

基金项目：

国家重点研发计划项目（2022YFC3002703）；中国长江三峡集团有限公司科研项目（0704221）；国家自然科学基金项目（52309004，U2340205）

作者简介：

仇红亚，男，工程师，博士，主要从事水文水资源研究。E-mail：qiu_hongya@ctg.com.cn

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2025） 01-0022-09

引用本文：

仇红亚，刘亚新，李妍清，等.

水库泄流洪水波在宜昌—大通河段传播规律研究

［J］.人民长江，2025，56（1）：22-30.

0" 引 言

水库泄流洪水波传播是当前水利工程和防洪管理中备受关注的问题［1-3］。研究人员针对该领域展开了一系列研究工作，其中数值模拟成为研究的主要方法之一［4-5］。近年来，数学模型在水库泄流洪水波传播领域的应用研究取得了多项进展。例如，基于复杂的水动力模型和地形数据，研究者能够更精确地预测洪水波的扩散和淹没范围，从而提前进行预警和采取应对措施［6］。同时，部分模型还考虑了水库泄流对水质的影响，如泥沙输移和水质变化，这对水资源保护和环境管理尤为重要。

随着计算能力和数据处理技术的提升，数学模型不断发展，从简化模型向复杂的耦合系统模型过渡，增强了对不同调度条件下水库泄洪过程的理解和预测能力［7-8］。通过建立数学模型，研究人员可以在不同尺度和复杂情景下进行模拟和预测，为防洪管理决策提供科学依据［9-10］。此外，数学模型方法还能够充分发挥计算机技术的优势，实现洪水波传播过程的快速、大规模计算，并且在一定程度上弥补了野外实验难以覆盖各种情况的局限性［11］。因此，数学模型方法在水库泄流洪水波传播规律研究中具有重要意义，为解决实际工程和管理问题提供了强有力的支持。

随着长江流域梯级水资源的开发，特别是三峡水库蓄水运用以来，长江水文情势发生了显著的变化［12-13］。水库进行应急抢险或是紧急防洪调度这一过程经常会引起泄流洪水在短时间内发生较大变化，甚至形成急变洪水波，而急变洪水波大多伴随着断波的形成［14-15］。程海云等［16］分析了三峡水库运行后荆江河段洪水传播时间特性，并进一步揭示了断波洪水与沙市站水位流量关系的响应规律。鉴于目前已有研究成果仅限于长江中下游荆江河段，泄流洪水波在螺山站以下河段传播特性有待进一步研究，因此有必要深入研究洪水波传播时间和传播距离以及削减过程等动力特征。本文以长江宜昌至大通干流河段为例，通过构建一维水动力学模型，模拟不同工况下水库泄流洪水波的传播特性，并分析其演进规律，以为区域防洪管理提供参考。

1" 一维水动力学模型构建

1.1" 研究区域

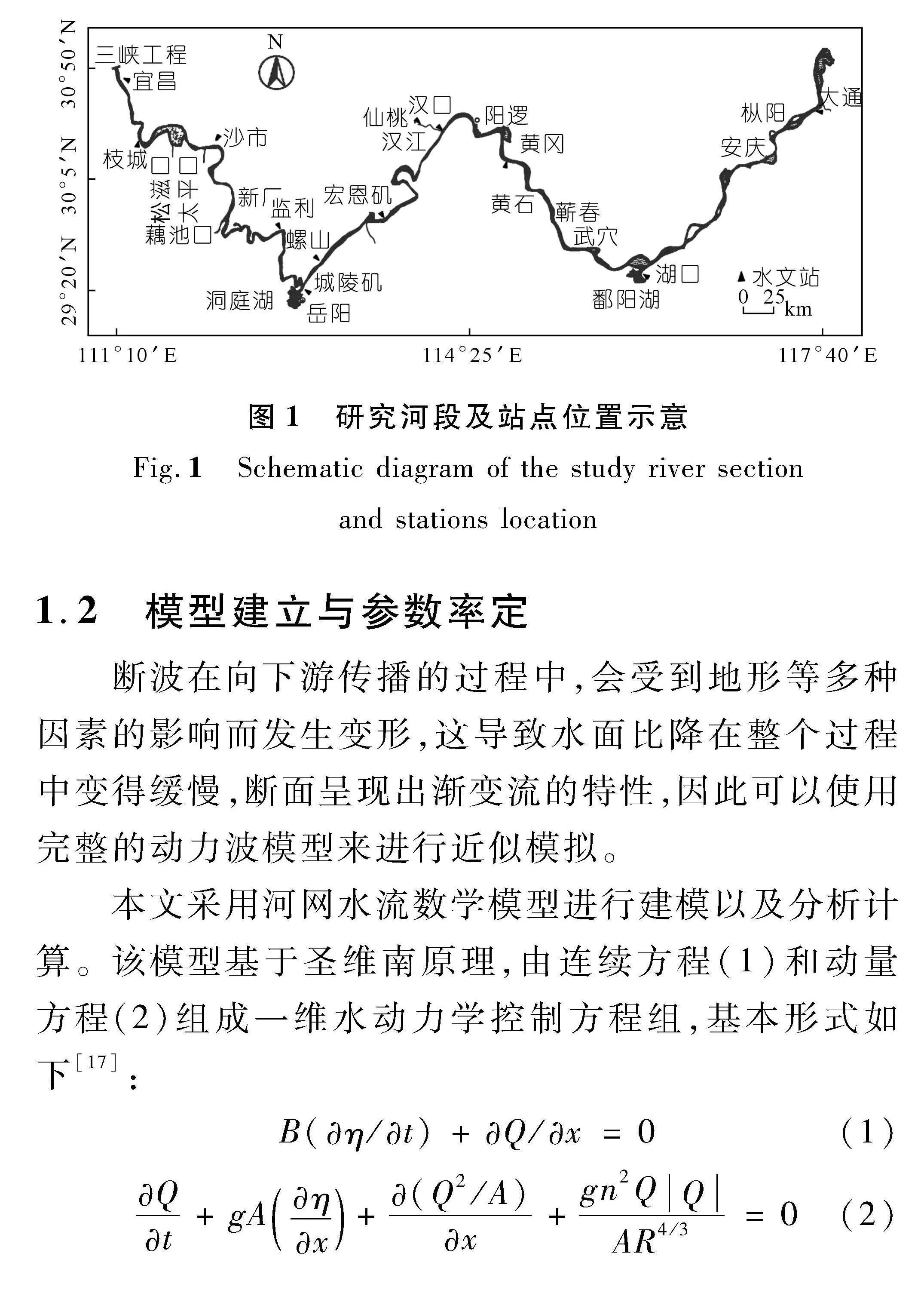
本次研究以长江宜昌至大通干流河段为研究对象。该河段长约1 183 km，其中宜昌至湖口为中游河段，沿程有清江、洞庭湖、汉江、鄱阳湖及其他支流入汇；湖口至大通河段为长江下游的一部分，长约228 km，该河段基本不受潮汐影响。宜昌至大通干流河段所处地理位置及重要站点分布如图1所示。

1.2" 模型建立与参数率定

断波在向下游传播的过程中，会受到地形等多种因素的影响而发生变形，这导致水面比降在整个过程中变得缓慢，断面呈现出渐变流的特性，因此可以使用完整的动力波模型来进行近似模拟。

本文采用河网水流数学模型进行建模以及分析计算。该模型基于圣维南原理，由连续方程（1）和动量方程（2）组成一维水动力学控制方程组，基本形式如下［17］：

B（η/t）+Q/x=0

（1）

Qt+gAηx+（Q2/A）x+gn2QQAR4/3=0

（2）

式中：B为断面水面宽度，m；

η为断面中心水位，m；

t为时间，s；

Q为断面流量，m3/s；

x为距离，m；

g为重力加速度，m/s2；

A为过水断面面积，m2；

n为河道综合糙率；

R为断面水力半径，m。

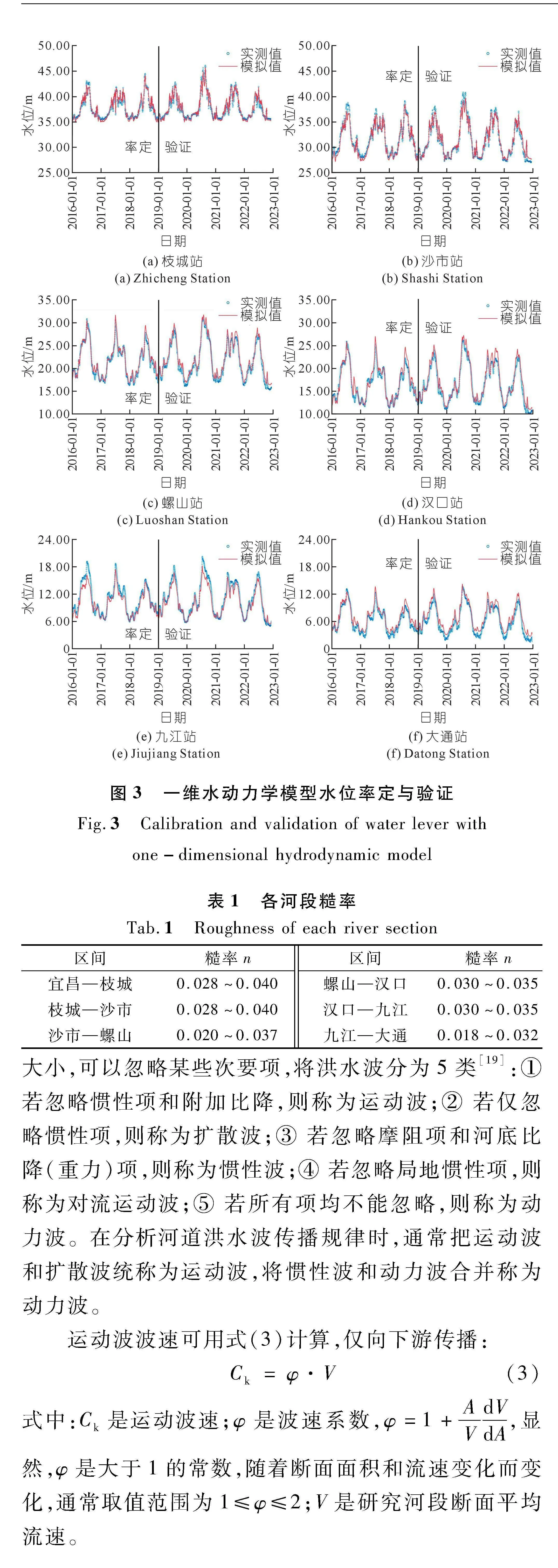
采用2020年实测断面资料对研究区域建模，在宜昌—大通干流河段设置927个断面，断面间距为0.24～7.89 km。采用宜昌站流量过程作为模型计算上边界，下边界采用大通站水位-流量关系曲线，区间入汇的包括清江、洞庭湖、汉江和鄱阳湖等水系，模型中采用支流入汇流量过程。结合地形数据，选取2016～2018年实测数据进行参数率定，2019～2022年实测数据进行验证。图2～3为各站流量与水位率定与验证结果，率定验证完成后各个河段糙率见表1。由图2～3及表1可知，各站点流量、水位过程的验证结果良好，模型参数合理，可用于宜昌—大通河段洪水特性分析计算［18］。

2" 宜昌—大通河段洪水波传播特性分析

2.1" 波速计算

根据圣维南动力方程中各项的对比关系和数量级

大小，可以忽略某些次要项，将洪水波分为5类［19］：① 若忽略惯性项和附加比降，则称为运动波；② 若仅忽略惯性项，则称为扩散波；③ 若忽略摩阻项和河底比降（重力）项，则称为惯性波；④ 若忽略局地惯性项，则称为对流运动波；⑤ 若所有项均不能忽略，则称为动力波。在分析河道洪水波传播规律时，通常把运动波和扩散波统称为运动波，将惯性波和动力波合并称为动力波。

运动波波速可用式（3）计算，仅向下游传播：

Ck=φ·V（3）

式中：Ck是运动波速；

φ是波速系数，φ=1+AVdVdA，显然，φ是大于1的常数，随着断面面积和流速变化而变化，通常取值范围为1≤φ≤2；V是研究河段断面平均流速。

动力波的波速计算如式（4）：

Cd=V+gh

（4）

式中：Cd是动力波波速；

g是重力加速度；

h是研究断面平均水深。动力波可沿上下游两个特征方向传播，同流量条件下动力波波速一般大于运动波波速。大多数河道水流运动属于运动波范畴，但在流量发生急剧变化时波型也会发生相应的转换。

2.2" 洪水波形变指数

洪水波传播过程中，波形不断发生变化，对于洪水过境的每一个断面都会出现一个涨水过程和退水过程，涨水过程的流量变率坡度如下：

dQdt=Qp-Qitp-ti

（5）

据此，引入洪水波形变指数［20］：

FI=（Qp-Qi）/Qi（tp-ti）/Δt

（6）

式中：Qp是洪峰流量;

Qi是洪水起涨流量;

tp是洪峰出现时的时间;

ti是洪水起涨时的时间;

Δt是时间差，此处为1 h。FI越接近0，洪水过程越平稳，数值越大洪水波动越剧烈。

2.3" 研究方案和计算工况

（1） 不同断波流量计算方案。

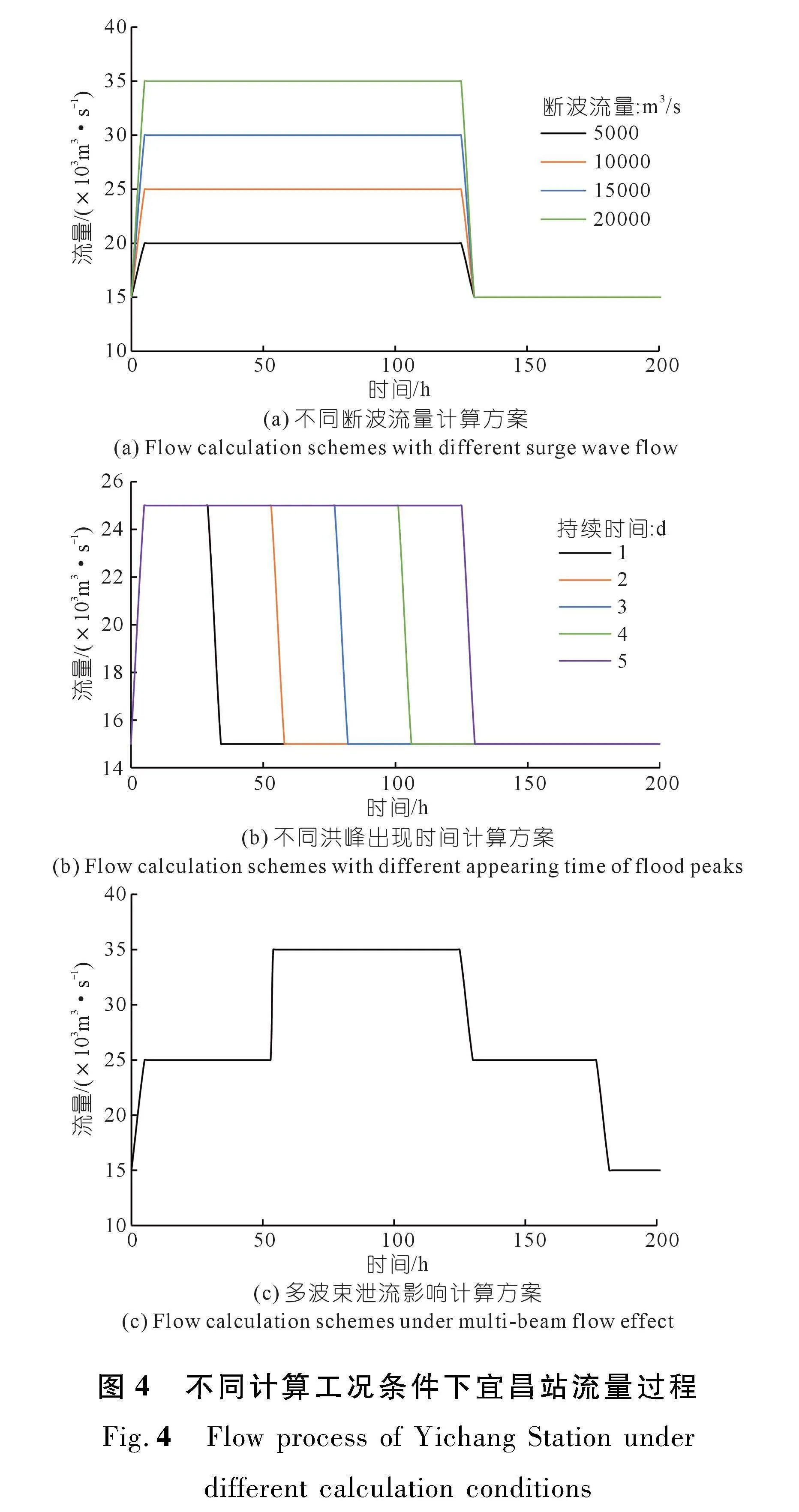
根据三峡水库和葛洲坝枢纽出库流量的系列统计数据，计算模型上边界宜昌站恒定流流量取15 000 m3/s，假定在5 h内流量分别骤增至 2 0000，25 000，30 000，35 000 m3/s，即出现断波流量分别为5 000，10 000，15 000，20 000 m3/s，增加后的流量持续5 d后，在5 h内再骤减至15 000 m3/s，图4（a）为4组断波流量出现过程，其中支流清江、洞庭湖、汉江和鄱阳湖来水分别按照无入流和近10 a汛期平均流量两个方案计算。

（2） 不同洪峰持续时间计算方案。

假设宜昌站以15 000 m3/s的恒定流起涨流量开始计算，假定在5 h内流量骤增至 25 000 m3/s，增加后流量再分别持续1，2，3，4，5 d后，再在5 h内骤减至15 000 m3/s，共计5 组不同历时的断波洪水过程（图4（b）），其中支流清江、洞庭湖、汉江和鄱阳湖来水分别按照无入流和近10 a汛期平均流量两个方案计算。

（3） 多波束泄流影响计算方案。

假设宜昌站以15 000 m3/s的恒定流起涨流量开始计算，假定在5 h内流量骤增至 25 000 m3/s，流量持续2 d后，再施放一组10 000 m3/s的断波洪水过程，两组洪峰持续3 d后在5 h内骤减至25 000 m3/s，继续持续2 d后再在5 h 内骤减至15 000 m3/s，考察这2组断波洪水的传播过程（图4（c）），其中支流清江、洞庭湖、汉江和鄱阳湖来水分别按照无入流和近10 a汛期平均流量两个方案计算。

2.4" 结果与分析

2.4.1" 不同断波流量的影响

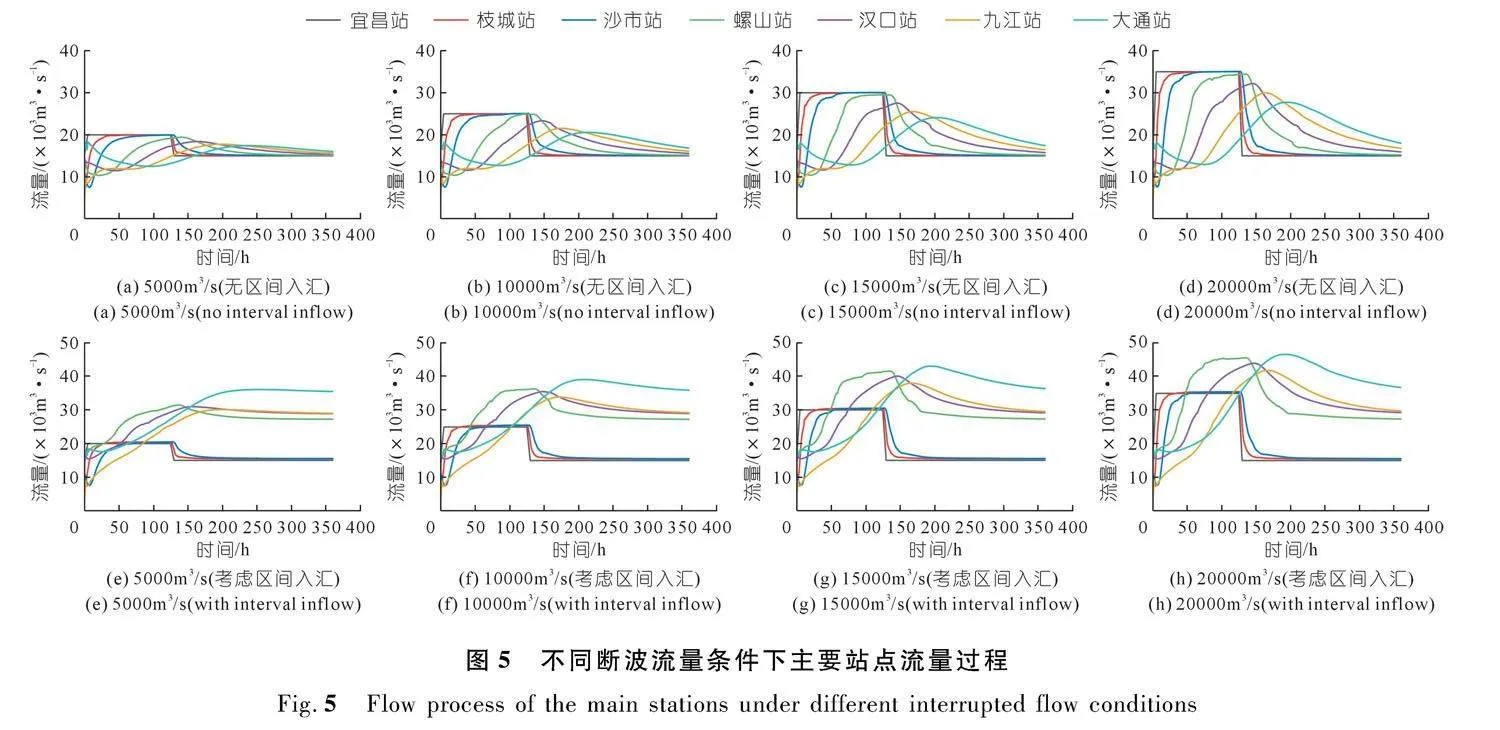
洪峰流量大小通常对下游防洪形势有着重要影响。对比不同断波流量条件下洪水波的传播规律（图5），发现同一流量条件下，沙市站以上河段洪峰流量基本无削减，仅持续时间存在不同程度减少。当断波流量为5 000 m3/s时，枝城和沙市站洪峰持续时间分别从5 d降至73.85 h和23.80 h；随着距离的增加洪峰坦化作用越明显，螺山、汉口、九江和大通站洪峰分别削减了2.88%，7.95%，11.25%和12.88%。然而，随着断波流量的增加，洪峰沿程坦化过程加剧，当断波流量为15 000 m3/s时，螺山、汉口、九江和大通站洪峰分别削减了3.55%，8.25%，14.96%和19.73%。

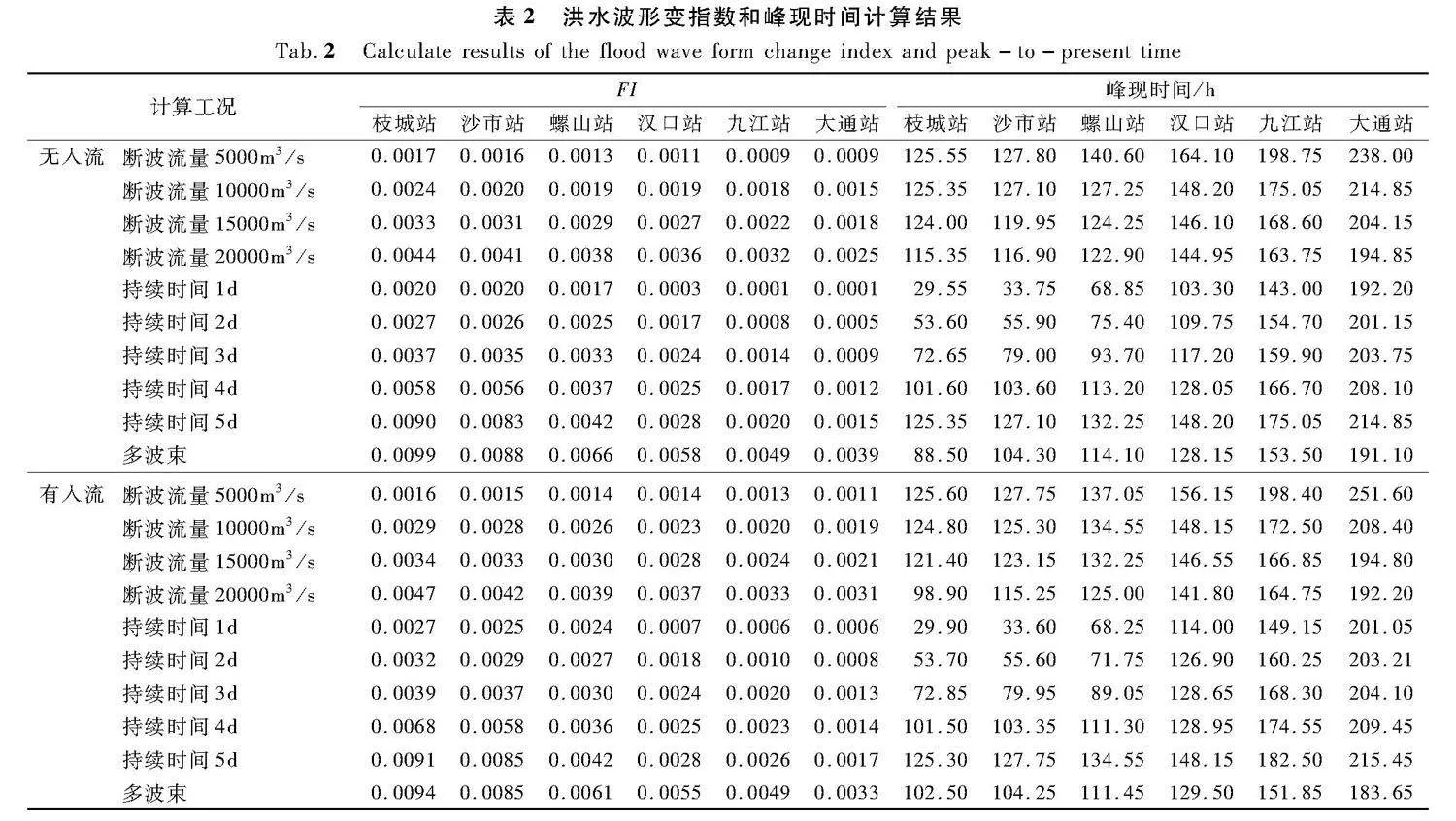
当断波流量增加，下游各站点的峰现时间均出现不同程度提前，以汉口站为例，当断波流量为5 000 m3/s时，峰现时间出现在164.10 h，当断波流量分别为10 000，15 000，20 000 m3/s时，峰现时间分别为148.20，146.10，144.95 h。此外，当有支流入汇时，洪水波传播过程会更加复杂，支流的入汇导致洪峰流量在观测站点出现了不同程度的增加，其中洞庭湖和鄱阳湖的入汇导致螺山和大通站的洪峰流量不同程度增加，洪峰持续时间更长。从表2可见，随着断波流量的增加，同一站点洪水波形变指数急剧增加，表明洪水波动越剧烈；随着沿程距离的增加洪水波形变指数递减，表明波峰在不断的削减，但高流量的断波洪水在同一站点仍存在较大的形变指数。

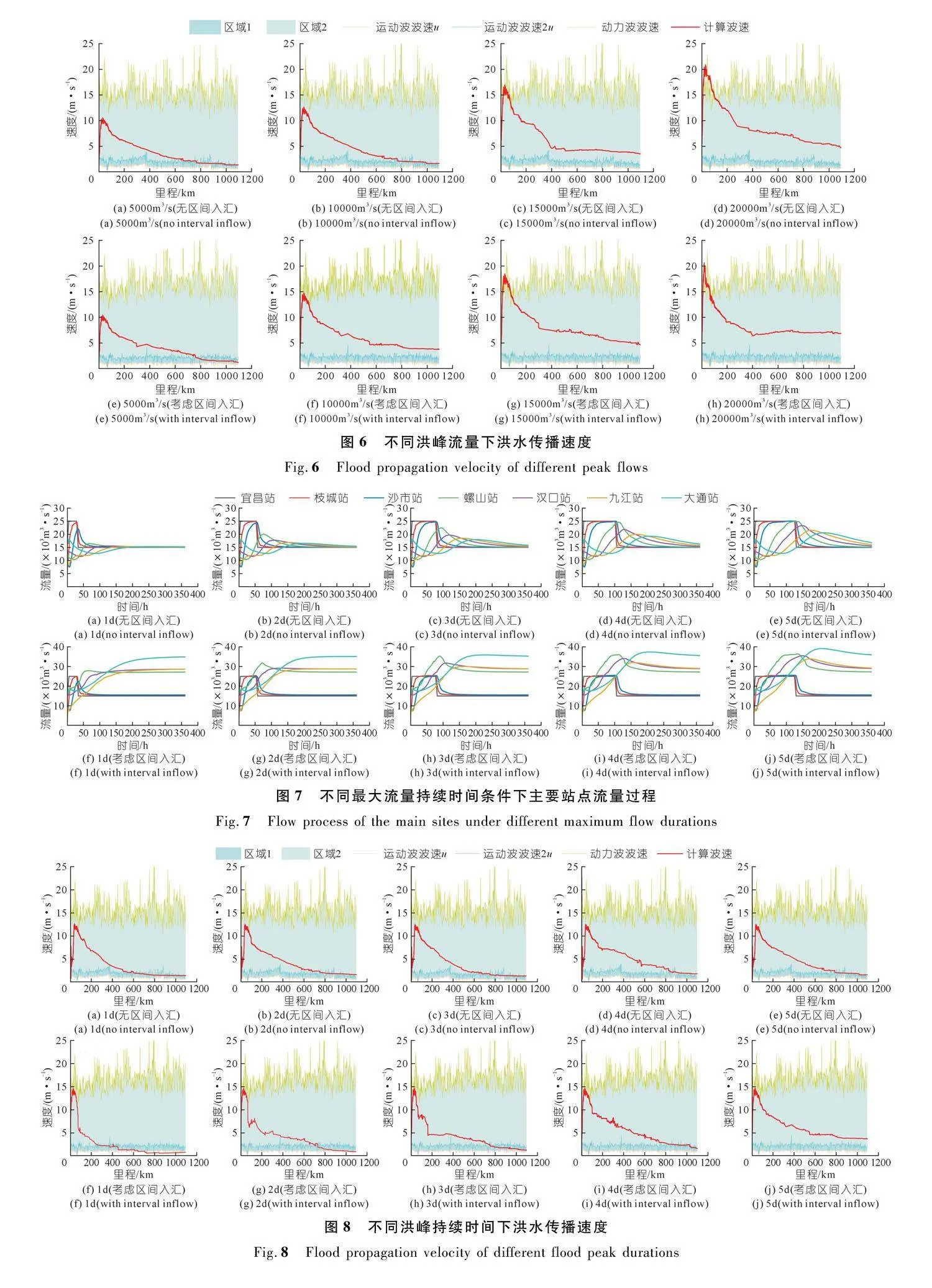
根据宜昌—大通河段模型断面间的河道里程和洪

峰在断面间的过境时间差，计算得出沿程断波传播波

速，并与运动波和动力波的计算波速对比分析，结果如图6所示。当无区间支流入汇，宜昌站出现断波流量为5 000 m3/s 和10 000 m3/s时，计算波速在宜昌站以下750 km内均大于2u（u为运动波波速），但仍小于计算动力波速Cd，传播特性符合过渡区洪水过程；750 km以下至大通河段，计算运动波速Ck基本处于运动波波速Ck范围（1u≤Ck≤2u），符合运动波传播特性；而当断波流量达到15 000 m3/s以上时，宜昌站以下约150 km范围内，计算波速在动力波速上下变化，表现出动力波传播特性，150 km以下范围至大通河段，计算波速大于2u，小于动力波速Cd，表现为过渡区洪水波特性。当有区间支流入汇，计算波速表现出类似变化，所不同的是当断波流量为10 000 m3/s时，宜昌站以下河段计算波速均大于2u，已无符合运动波传播河段。

2.4.2" 不同洪峰流量持续时间的影响

上游洪水持续时间是预测评估下游可能的洪涝灾害的重要指标。不同的上游可能洪水持续时间在下游的洪水演进过程计算结果如图7所示。在无区间入流条件下，上游洪峰持续时间越长，下游观测站点的洪峰流量越大，且洪峰的削减过程越缓慢，例如宜昌站洪峰流量持续1 d时，枝城、沙市、螺山、汉口、九江和大通站分别出现峰值流量为24 600，22 100，16 400，15 600，15 300 m3/s和15 300 m3/s，峰现时间分别为29.55，33.75，68.85，103.30，143.00 h和192.20 h，而当洪水持续时间延长到5 d时，以上各站点的峰值流量为

2 500，25 100，24 900，23 300，21 500 m3/s和20 600 m3/s，峰现时间分别为125.35，127.10，132.25，148.20，175.05 h和214.85 h。可见，在相同的洪峰流量条件下，延长上游洪水的持续时间可导致下游洪峰的大幅提高和历时的增加。

此外，通过对比有区间支流入汇情况可见，支流的来流不同程度增加了观测站点洪峰流量，随着上游洪水历时的延长，支流汇入情况下洪水在各站点的洪水历时大幅延长，洪峰流量增加了1.12%～127.78%。从表2可见，随着洪峰持续时间的增加，同一站点洪水波形变指数急剧增加，表明洪水波动越剧烈;随着沿程距离的增加洪水波形变指数递减，表明波峰也在不断的削减，但洪峰持续时间越长形变指数衰减越慢。

计算波速结果如图8所示，当无区间支流入汇，计算波速在宜昌站以下均大于u，随着洪峰持续时间的延长，宜昌站以下处于运动波传播状态的河段距离也随之减少，当洪峰流量分别持续1，2，3，4 d和5 d时，计算波速分别在宜昌站以下550，670，740，810 km和880 km处进入到（u，2u）范围内，在该范围内的洪水波符合运动波传播规律，其余上游河段计算波速大于2u，在绝大部分河段小于动力波速Cd，传播特性符合过渡区洪水过程。当有区间支流入汇，计算波速表现出类似变化，所不同的是当断波持续时间达到5 d时，宜昌站以下河段计算波速均大于2u，已无符合运动波传播河段。

2.4.3" 多波束断波传播特征分析

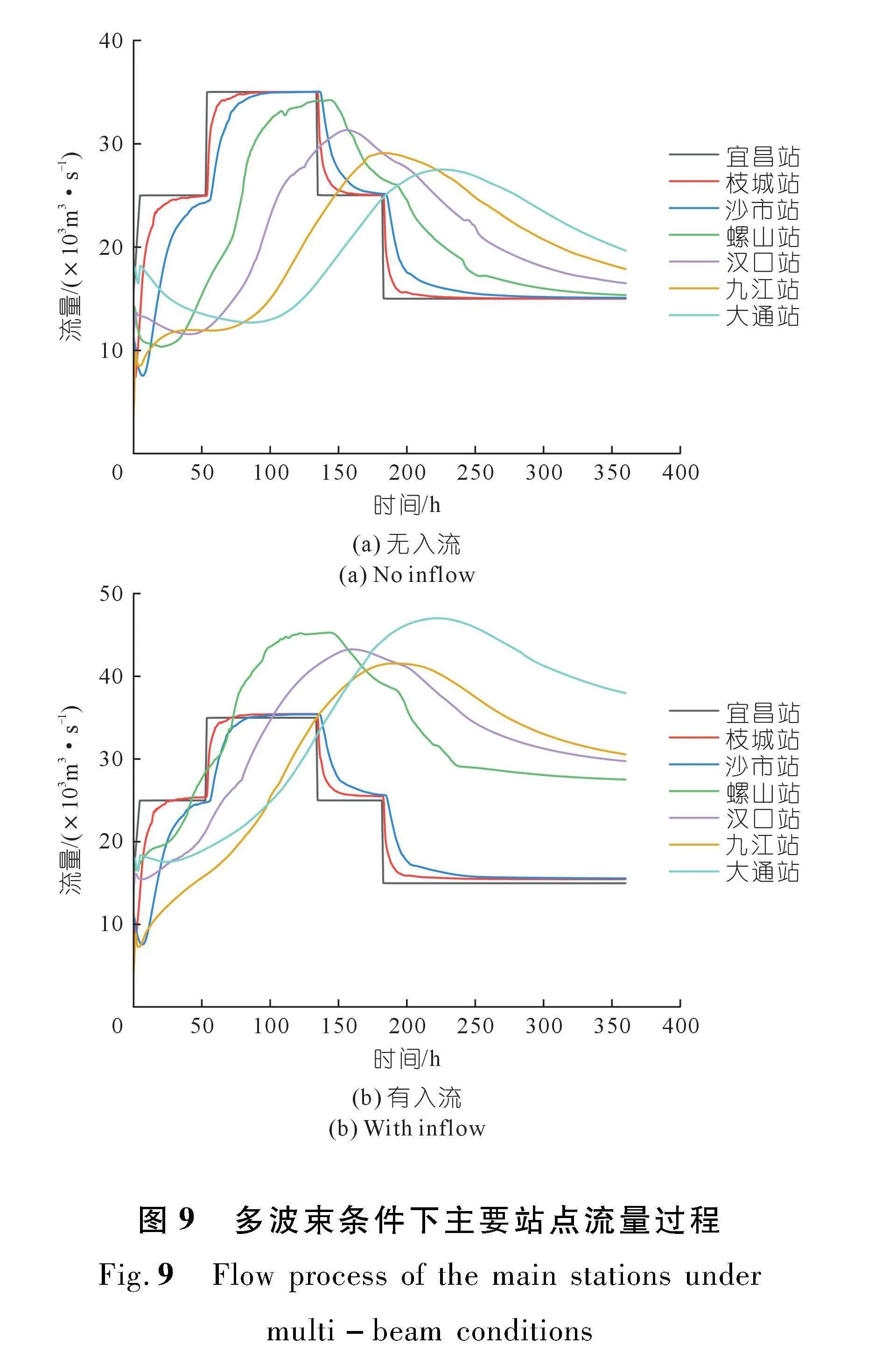
在上游梯级水库调度的过程中，水库下游通常会产生系列的间断波束，多波束的传播增加了下游水流的非恒定特性。对比多波束条件下洪水波的传播过程，发现间隔出现的断波波束在沿程传播过程中会不断坦化融合，在宜昌站的阶梯状断波流量过程传播到螺山站时流量曲线已不再明显弯折，汉口站及以下基本呈现单波束形态（图9）。无论是涨水波还是退水波，随着距离的增加断波效应均逐渐减弱，洪峰减小，历时延长，螺山、汉口、九江和大通站洪峰分别削减了2.24%，10.56%，16.85%和21.47%。当有支流入汇时，沿程站点洪峰流量变化表现出明显的非一致性，支流水流的汇入不同程度地增加了支流入汇处下游站点的洪峰流量，且高流量历时明显延长。从表2可见，随着沿程距离的增加洪水波形变指数递减，表明波峰在不断的削减，但多波束传播条件下形变指数沿程衰减过程明显放缓。

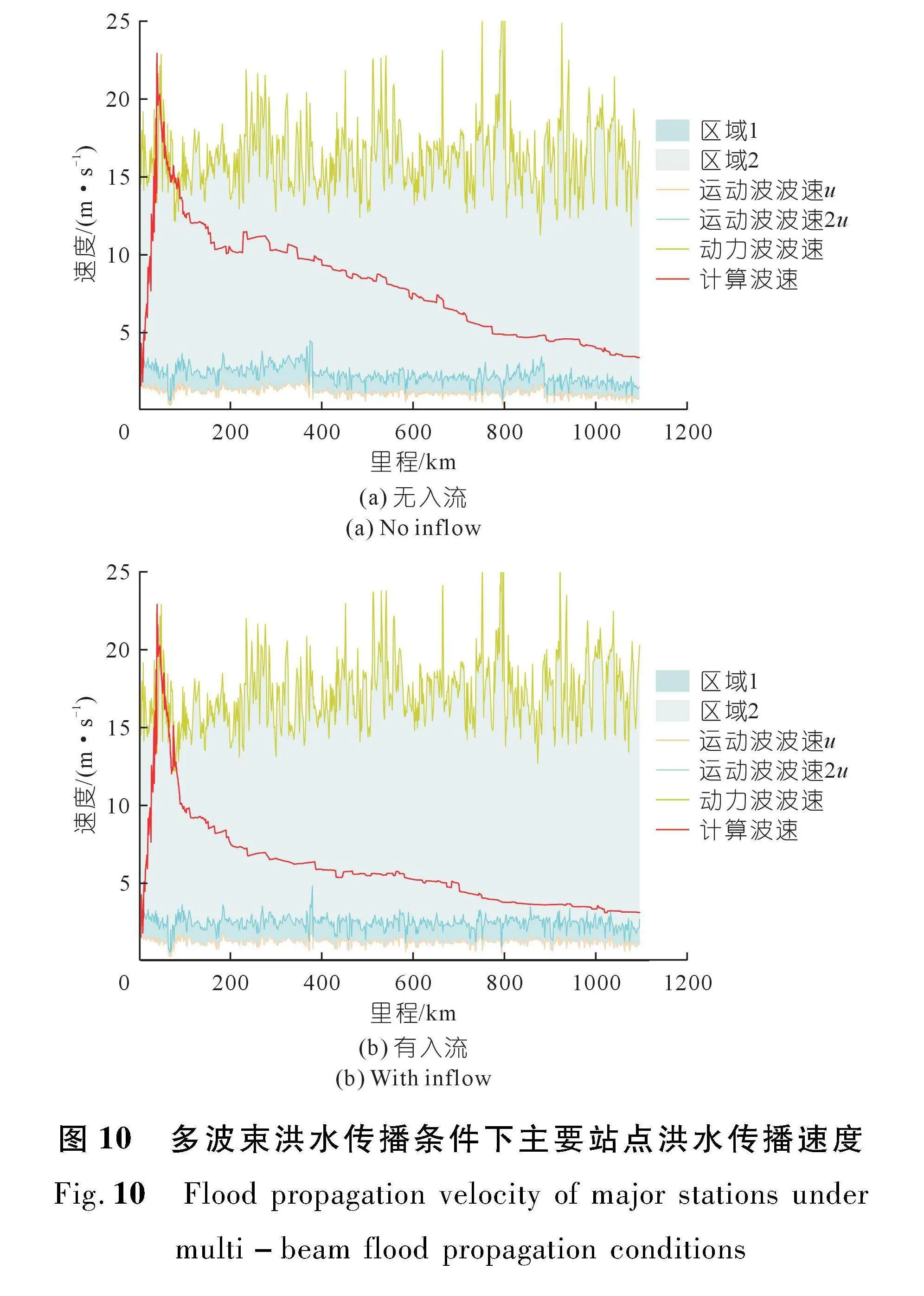
多波束断波条件下计算波速结果如图10所示，当无区间支流入汇，计算波速在宜昌站以下河段均大于2u，无符合运动波传播河段。在宜昌站以下180 km内计算波速在动力波速Cd上下波动，该河段洪水运动符合动力波传播规律，其余河段计算波速符合过渡区洪水运动规律。当有区间支流入汇，计算波速表现出类似变化。

3" 结 论

通过对长江宜昌至大通河段水库泄流洪水波传播的深入研究，本文构建了一维水动力学模型并进行了详细分析。通过模拟对比不同水库泄流洪水波与运动波和动力波的传播规律，得出以下主要结论：

（1） 当水库在短时间内下泄流量急剧变化时，即断波形成后，随着断波流量增加，下游各站点的峰现时间不同程度提前，越靠下游峰现时间变化越大；断波流量每增加5 000 m3/s，各站点峰现时间平均提前约7.5 h，当断波流量增加到1 5000 m3/s时，宜昌至大通绝大部分河段洪水波运动符合过渡区洪水波特性，局部表现为动力波特性；随着断波流量的增加，同一站点洪水波形变指数急剧增加，并且断波流量越大，形变指数衰减越慢。

（2） 随着断波流量持续时间的延长，下游各站点洪峰流量不同程度增加，越靠下游站点洪峰增加越大；同时断波流量持续时间的延长也推迟了各站点的峰现时间，但峰现时间的影响是越靠下游站点影响越小；断波流量持续时间越长，符合运动波传播规律的河段距离越短；随着洪峰持续时间的增加，洪水波的形变指数衰减速度变缓。

（3） 水库下游产生的系列间断波束增加了下游水流的非恒定特性，对比多波束条件下洪水波的传播过程，发现间隔出现的断波波束在沿程传播过程中会不断坦化融合，随着距离的增加断波效应均逐渐减弱，计算波速普遍较高，全河段无符合运动波传播范围，随着沿程距离的增加洪水波形变指数递减，但多波束传播条件下形变指数沿程衰减过程明显放缓。

需要指出的是，当有支流入汇时，以上3种条件下的沿程站点洪峰流量变化均表现出明显的非一致性，支流水流的汇入不同程度地增加了支流入汇的下游站点的洪峰流量，且高流量历时明显延长。洪水波形变指数也随着支流汇入的大小和沿程距离的变化而发生调整，但总的演化趋势和无支流汇入情况一致。本研究不仅深化了对长江下游水库泄流洪水波传播规律的理解，也为实际工程和管理决策提供了重要的技术支持。未来的研究可以进一步结合更多实测数据和复杂水文条件，揭示断波洪水的形成和演进机制，以应对日益复杂的洪水风险管理挑战。

参考文献：

［1］" MANUELA I B，PHILIPPE N.Spatial variability in Alpine Reservoir regulation：deriving reservoir operations fromstreamflow using generalized additive models［J］.Hydrology and Earth System Sciences，2023，27（3）：673-687.

［2］" 张建云，盛金保，金君良，等.全国水库大坝应急管理存在问题和对策建议［J］.中国应急管理科学，2022（9）：23-30.

［3］" 卢程伟.流域水库群蓄滞洪区综合防洪调度研究与应用［D］.武汉：华中科技大学，2019.

［4］" 胡琼方，李秋平，邹涛，等.三峡出库急变洪水波传播规律及其对水文测报的影响［J］.水利水电快报，2019，40（2）：1-5，25.

［5］" 程海云，陈力，许银山.断波及其在上荆江河段传播特性研究［J］.人民长江，2016，47（21）：30-34.

［6］" 卢程伟，陈莫非，张余龙，等.断波在朱沱—三峡坝址库区河段传播规律分析［J］.长江科学院院报，2021，38（8）：14-18，24.

［7］" 张茜.佛子岭水库泄洪洪水演进模拟研究［D］.淮南：安徽理工大学，2020.

［8］" 王丽学，林凤伟，汪可欣，等.基于蒙特卡罗模拟的泄洪风险率计算［J］.人民长江，2008，39（19）：20-22.

［9］" TENG J，JAKEMAN A J，VAZE J，et al.Flood inundation modelling：a review of methods，recent advances and uncertainty analysis［J］.Environmental Modelling amp; Software，2017，90：201-216.

［10］王丽萍，张验科，纪昌明，等.模拟最大熵法及其在水库泄洪风险计算中的应用［J］.水利学报，2011，42（1）：27-32.

［11］高帅领，夏军强，董柏良，等.雨水口泄流对城市洪涝影响的数学模型［J］.浙江大学学报（工学版），2022（3）：590-597.

［12］邴建平，邓鹏鑫，张冬冬，等.三峡水库运行对鄱阳湖江湖水文情势的影响［J］.人民长江，2020，51（3）：87-93.

［13］徐长江，徐高洪，戴明龙，等.三峡水库蓄水期洞庭湖区水文情势变化研究［J］.人民长江，2019，50（2）：6-12.

［14］李晓昭.基于MIKE11的三峡库区洪水波传播规律研究［D］.武汉：华中科技大学，2018.

［15］孙立刚，李国定，陈金海，等.“东方之星”轮翻沉事件再现仿真系统研究［J］.中国水运（下半月），2016，16（6）：78-80，153.

［16］程海云，陈力.三峡水库泄水波与沙市站水位流量响应关系研究［J］.人民长江，2017，48（19）：29-34，41.

［17］DHI.A modelling system for rivers and channels：reference manual［R］.Denmark：DHI Water amp; Environment，2004.

［18］张冬冬，戴明龙，徐高洪，等.三峡水库蓄水期洞庭湖出湖水量变化［J］.水科学进展，2019，30（5）：613-622.

［19］程思学.基于KdV-Burgers型方程的非破碎涌波生成理论研究［D］.杭州：浙江大学，2022.

［20］DIPSIKHA D，ANUPAL B，ARUP K S.Characterization of dam-impacted flood hydrograph and its degree of severity as a potential hazard［J］.Natural Hazards，2022，112（3）：1989-2011.

（编辑：郭甜甜）

Propagation law of reservoir flood wave in main channel of Changjiang River from Yichang to Datong section

QIU Hongya1，LIU Yaxin1，2，3，LI Yanqing4，ZHANG Dongdong4，XIONG Feng4

（1.China Three Gorges Corporation，Yichang 443133，China;

2.China Yangtze Power Co.，Ltd.，Yichang 443002，China；

3.Hubei Provincial Key Laboratory of Wisdom Yangtze River and Hydropower Science，Yichang 443002，China；

4.Bureau of Hydrology，Changjiang Water Resources Commission，Wuhan 430010，China）

Abstract：

In current water conservancy engineering and flood management，the propagation of flood waves from reservoir discharge is a matter of great concern.Taking the Yichang-Datong section in main channel of Changjiang River as an example，a one-dimensional hydrodynamic model was constructed to simulate the propagation characteristics of flood waves under different working conditions and to compare and analyze the flood evolution patterns along the course.The research results show that：① The formation of break wave floods can shorten the peak arrival time in downstream sections to varying degrees.With the increase of break wave flow，the distance of river sections where flood waves propagate as kinematic waves significantly shortens，and the flood wave deformation index increases；② With the extension of the duration of peak flood flow，the distance of flood wave propagation with kinematic wave characteristics will also be shortened，and the flood wave deformation index will increase.However，the peak arrival time at the same site or a certain mileage will be delayed，and the duration of the peak flood will be extended；③ Under multi-beam break wave conditions，the calculated wave speed is generally higher.As the distance along the course increases，the deformation index declines，but the decay process of the deformation index along the course under multi-beam propagation conditions is significantly slowed down；④ When there are tributary inflows，the changes in peak flow at sites along the course all exhibit significant inconsistencies，and the duration of high flow is significantly extended.The research findings are of great significance for revealing the propagation laws of flood waves from reservoir discharge and can provide references for regional flood management.

Key words：

reservoir release； flood wave； propagation characteristics； deformation index； hydrodynamic model； Changjiang River