基于改进免疫遗传算法的铁路空箱调运优化

摘" 要：针对空箱调运问题，在传统免疫遗传算法（Immune Genetic Algorithm， IGA）基础上，通过对Hamming距离计算方式优化与调整，获得抗体亲和度与抗体浓度的精确度量，并据此设计了改进免疫遗传算法（Improved Immune Genetic Algorithm， IIGA）。为验证该算法的有效性和优势，以兰州铁路局下辖的各集装箱办理站实际运输数据为例，分别将所提出的IIGA与传统IGA、遗传算法（Genetic Algorithm， GA）设计对比实验。结果表明：在解决空箱调运问题时，相较于传统IGA与GA，IIGA能够在相对较短的时间内，以最少的迭代次数迅速收敛至最优解。

" 关键词：改进免疫遗传算法；空箱调运；集装箱；Hamming距离；亲和度

" 中图分类号：F253" " 文献标志码：A

DOI：10.13714/j.cnki.1002-3100.2025.03.028

Abstract： Addressing the issue of empty container repositioning， an Improved Immune Genetic Algorithm（IIGA）was developed based on the traditional Immune Genetic Algorithm（IGA）by optimizing and adjusting the calculation method for Hamming distance to achieve precise measurements of antibody affinity and antibody concentration. To validate the effectiveness and advantages of this algorithm， a comparative experiment was designed using actual transportation data from various container terminals under the jurisdiction of Lanzhou Railway Bureau， comparing the proposed IIGA with traditional IGA and Genetic Algorithm（GA）. The results indicated that， when solving the problem of empty container repositioning，IIGA was able to converge to the optimal solution more rapidly with the least number of iterations within a relatively shorter period of time compared to traditional IGA and GA.

Key words： Improved Immune Genetic Algorithm; empty container repositioning; container; Hamming distance; affinity

0" 引" 言

" 随着铁路需求的增长，集装箱运输作为一种高效、环保的运输方式，在物流体系中扮演着越来越重要的角色。然而，在实际运营过程中，空箱调运问题一直是困扰铁路集装箱运输效率提升的难题之一。空箱调运不仅涉及到运输成本的控制，还关系到集装箱资源的有效配置和物流服务的及时性。因此，如何科学、高效地解决空箱调运问题，对于提升铁路集装箱运输的整体效益具有重要意义。

" 空箱调运问题一直以来是国内外学者研究的重点。孙浩[1]通过运用整数规划方法优化空箱海陆多式联运调运成本，证明了模型有效可行。邬开俊等[2]提出一种自适应变异粒子群算法（Adaptive Mutation Particle Swarm Algorithm）求解铁路空车调配问题，通过调整变异概率和惯性权重因子优化空车总走行距离。段刚等[3]针对铁路集装箱运输的空箱调运问题，设计遗传算法（Genetic Algorithm）并验证其高效性与多最优解获取能力。Huang[4]从降低成本角度优化空箱调运，运用线性规划方法建立模型并举例验证，为单件低价商品问题提供新的定量分析方法。Meng et al.[5]提出结合集线式、多港挂靠及空箱调运的班轮服务网络设计问题，并通过CPLEX求解混合整数线性规划模型证明其成本节约潜力。石红国等[6]提出基于运达时间约束的集装箱空箱随机机会模型，设计基于TOPSIS的限定参数区间搜索算法求解该模型。邢磊[7]针对可折叠集装箱应用、合作协议下空箱调运及需求不确定性问题，分别构建优化模型，设计混合遗传算法（Hybrid Genetic Algorithm）进行求解，提供中欧班列海陆协同调运、多周期动态优化及分布式鲁棒优化的解决方案。姜志永[8]针对两种不同的特种箱空箱调运模型，分别设计限定范围的帕累托最优解搜索算法（Pareto Optimal Solution Search Algorithm）和遗传算法求解。岳彦辰[9]对多周期内陆集装箱调运与库存优化问题进行深入分析，并设计改进变邻域搜索算法（Improved Variable Neighborhood Search Algorithm）进行求解。针对中欧班列的空箱管理问题，朱星龙等[10]全面考虑空箱获取过程中的调运费、装卸费、堆存费以及租赁费等相关因素，进而构建基于集装箱共享的班列公司的动态空箱调租优化模型，并使用Lingo软件内置的分支定界法对模型进行精确求解；胡广红等[11]通过设计免疫遗传算法（Immune Genetic Algorithm）进行优化求解，结果显示，相较于现行的空箱调运方案，采用集装箱共享模式能够显著降低空箱调运的总费用。Xu et al.[12]提出结合自适应机制的强化学习框架，用于优化海运物流中的空箱调运问题，通过动态调整奖励函数权重提高了问题解决性能。钱力[13]构建以计划周期内整个运输网络空箱调运总费用达到最小化为目标函数的铁路集装箱多时段空箱调运优化模型，运用李雅普诺夫（Lyapunov）优化方法简化该模型，进而利用数学软件进行求解。

" 本文基于免疫遗传算法的核心原理，通过对Hamming距离计算公式进行优化调整，提出改进免疫遗传算法（Improved Immune Genetic Algorithm， IIGA）。为验证该算法的性能，将其与传统免疫遗传算法及遗传算法进行对比。结果表明，IIGA在求解效率方面实现了显著提升。

1" 铁路集装箱空箱调运数学模型

" 空箱调运问题通常涉及解决如何以最有效或最低成本的方式将空箱从供应站调配到需求站的问题。设n为空箱供应站数量，A=a，a，…，a表示空箱供应站集合，c为供应站a可供应的空箱数量，其中i∈1，n；m为空箱需求站数量，B

=b，b，…，b为空箱需求站集合，则d表示需求站b所需空箱数量，其中j∈1，m。供应站a到需求站b的运输距离用d表示，x是决策变量，表示从供应站a到需求站b调运空箱数。建立满足以上要求的数学模型：

minZ=xd" " " " " " " " " " " " " " " " " " " " " " （1）

subject to：

x=c， i=1，2，…，n" " " " " " " " " " " " " " " " " " " " " " （2）

x=d， j=1，2，…，m" " " " " " " " " " " " " " " " " " " " " "（3）

x∈0，1，2，…" " " " " " " " " " " " " " " " " " " " " " "（4）

其中：式（1）为目标函数，旨在最小化整体运输费用；式（2）表示供应站a供应给各需求站的空箱数量之和恰好等于其供应量c；式（3）确保对于每个需求站b，从所有供应站a供应的空箱总数恰好满足其需求量d；式（4）为变量非负整数约束。

2" IIGA算法设计

2.1" 染色体编码

" 采用矩阵整数编码，以X表示一个染色体：

X=" " " " " " " " " " " " " " " " " " " " " " "（5）

式中：x为染色体基因，x∈0，1，2，…， i=1，2，…，n且j=1，2，…，m。

2.2" 亲和度计算算子

亲和度通常用来描述抗体与抗原之间的结合强度。在优化问题中，通常可以对函数值进行简单处理（如取倒数等）作为亲和度评价。此外，亲和度也能够通过更复杂的度量方式计算，例如Euclidean距离和Hamming距离，详见式（6）和式（7）。

H=" " " " " " " " " " " " " " " " " " " " " （6）

H=？鄣" " " " " " " " " " " " " " " " " " " " " " " "（7）

？鄣=" " " " " " " " " " " " " " " " " " " " " " （8）

式中：H表示抗体间结合强度；w和w分别表示抗体i的第k位和抗体j的第k位；L表示抗体编码长度。

" 针对空箱调运问题，对原有的式（8）进行优化调整得到式（9），然后通过Hamming公式计算抗体间的亲和度A。

？鄣=" " " " " " " " " " " " " " " （9）

A=" " " " " " " " " " " " " " " " " " " " " " " "（10）

2.3" 浓度计算算子

抗体浓度反应种群多样性。当抗体浓度过高时，意味着种群中存在大量相似个体，这种高度同质性不利于全局搜索。因此，有必要对这些高浓度的抗体实施适当的抑制措施，以促进种群的多样性和探索能力。相反，对于那些浓度较低的抗体，则应当给予适当的促进和激励，以增强其在搜索过程中的活跃度和贡献度。这样的策略有助于平衡种群的多样性和搜索效率，从而提升整体性能。抗体i的浓度CON计算公式为：

CON=S" " " " " " " " " " " " " " " " " " " " " " （11）

S=" " " " " " " " " " " " " " " " " " " " " （12）

其中：N为种群规模大小；S为抗体间相似度；λ为相似度阈值，一般取0lt;λlt;1。

2.4" 繁殖概率计算算子

抗体i的繁殖概率P通常需要综合考虑抗体适应度概率P与抗体浓度概率P。通常而言，具有高亲和度且浓度较低的抗体更容易被选择，以此确保后代种群的多样性得以保持。抗体繁殖概率计算公式为：

P=αP+1-αP" " " " " " " " " " " " " " " " " " " " " "（13）

P=" " " " " " " " " " " " " " " " " " " " " " " （14）

P=" " " " " " " " " " " " " " " " " " （15）

其中：0lt;αlt;1为亲和系数；f为抗体i的适应度值；0lt;ξlt;1为浓度阈值；0lt;tlt;N为浓度大于阈值的染色体数量。

2.5" 选择、交叉和变异算子

首先，按照个体繁殖概率，执行轮盘赌选择。

其次，随机选取两个父代染色体X和X，并生成一个随机数r∈0，1，若该随机数满足交叉概率条件，则依据参考文献[3]的方式生成子代染色体。这一过程将持续进行，直至种群中的所有父代染色体均被遍历完毕。其中X=x和X=x表示父代染色体，X=x和X=x表示生成的子代染色体。首先，令：

x=αx+1-γx" " " " " " " " " " " " " " " " " " " " "（16）

x=αx+1-γx" " " " " " " " " " " " " " " " " " " " "（17）

其中：0lt;γ≤0.5为交叉参数，x为maxy∈Z∪0|y≤x。再令：

x=max0， minαx+1-γx-x， αx+1-γx-x" " " " " " " " "（18）

x=max0， minαx+1-γx-x， αx+1-γx-x" " " " " " " " "（19）

其中：i=1，2，…，n且j=1，2，…，m，i和j不同时为1。当i=1，j≥2时，式（18）和式（19）中的最小值取第1项；反之，当j=1，i≥2时，两式中的最小值取第2项。以上计算方式能够保证调运量非负，且每行的调运量之和不会超过供应量，每列的调运量之和不会超过需求量，但供需平衡的条件不一定满足，因此，需要对调运量进行以下调整。以染色体X为例，令：

δ=minc-x， d-x" " " " " " " " " " " " " " " " " " （20）

然后令：x=δ+x更新x，遍历i和j，直至所有调运量都满足供需平衡条件。

" 最后，基于矩阵闭合回路法设计变异算子，对于某染色体X，挑选矩阵中不同行不同列的非零元素X和X，取：

Δ=minX，X" " " " " " " " " " " " " " " " " " " " " " （21）

然后根据以下方式执行变异操作。

X=X-Δ" " " " " " " " " " " " " " " " " " " " " " "（22）

X=X-Δ" " " " " " " " " " " " " " " " " " " " " " "（23）

X=X+Δ" " " " " " " " " " " " " " " " " " " " " " "（24）

X=X+Δ" " " " " " " " " " " " " " " " " " " " " " "（25）

2.6" 记忆库及终止准则

" 记忆细胞的主要功能是将表现优异的抗体后代储存于记忆库中，以便将来能够迅速响应相同的抗原挑战；设定最大迭代次数作为算法终止准则。

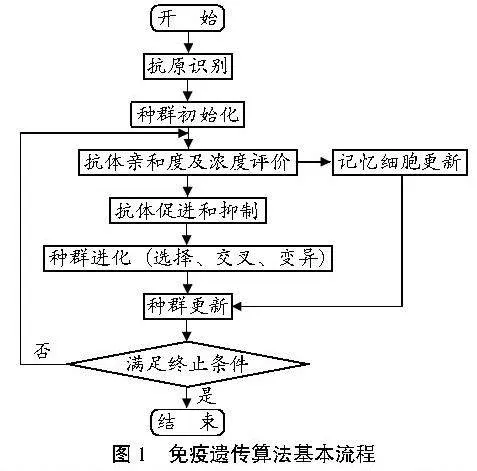
2.7" 算法流程

" 免疫遗传算法基本流程如图1所示。

（1）参数及种群初始化。输入各供应地的空箱供给量、需求地的空箱需求量及距离矩阵等基础数据。初始化算法关键参数，包括种群规模、记忆库容量、交叉概率、变异概率、亲和系数、相似度阈值、浓度阈值等。采用整数编码的方式初始化抗体群，随机生成满足供需平衡条件的初始抗体群。

" （2）抗体适应度、亲和度及浓度评价。

" （3）生成免疫记忆细胞，更新记忆库。

" （4）记录当前最佳个体适应度和种群平均适应度，更新全局最优解。

" （5）计算抗体繁殖概率。根据式（14）和式（15）分别计算抗体适应度概率P与抗体浓度概率P，进而通过式（13）得出抗体的繁殖概率P，为后续的选择操作提供依据。

（6）执行进化操作。根据抗体的繁殖概率执行选择操作，然后通过交叉和变异操作生成新的抗体群。同时，在生成新抗体群的过程中，加入记忆库细胞以加速算法的收敛速度。

" （7）判断终止条件。检查算法是否满足预设的终止准则。若满足，则结束循环，输出最终优化结果；否则，返回步骤（2）继续迭代。

3" 算例分析

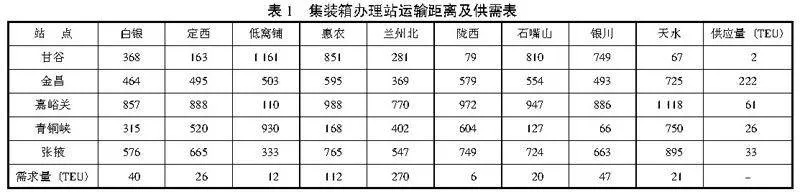
实验在CPU处理器为i5-12500H，主频2.50 GHz，内存16.0GB以及64位Windows11操作系统中，借助MATLAB R2022a软件执行。参考段刚等[3]的算例，选取甘谷、金昌、嘉峪关、青铜峡和张掖5个空箱供应站，以及白银、定西、低窝铺、惠农、兰州北、陇西、石嘴山、银川和天水9个空箱需求站。由于总空箱需求量（554TEU）大于总空箱供应量（334TEU），需增加一个虚拟供应站，其供应量为210TEU。各集装箱办理站间运输距离及供需量见表1。本实验所涉及的相关参数及具体配置已详细于表2中列出。

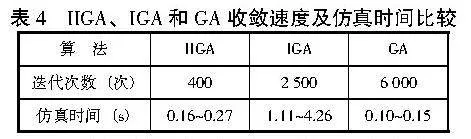
通过20次对比实验，评估IIGA、IGA及GA在解决空箱调运问题时的效率。确保在每次实验中算法都能够成功收敛至最优解（具体最优解见表3，对应最小适应度值为141 913），以此作为评估的前提和基础。表4记录了不同算法所需的迭代次数与仿真耗时数据。由表4可知：IIGA表现出了最快的收敛速度，其迭代次数显著低于其他两种算法，同时仿真耗时也相对较短；IGA的收敛速度介于IIGA和GA之间，仿真耗时相对较长；尽管GA在仿真耗时方面与IIGA具有较强的竞争力，但其收敛速度却明显滞后。

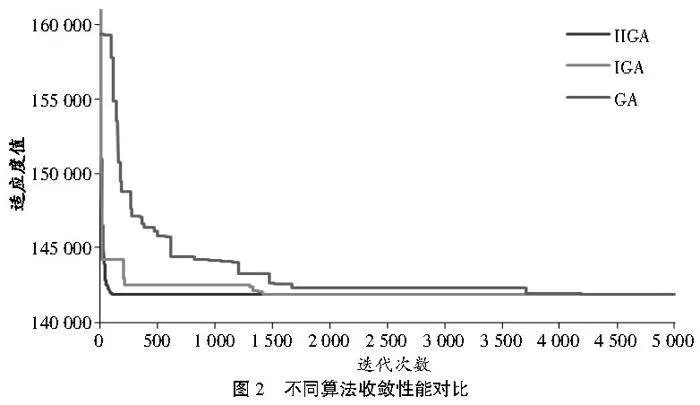
图2描绘了某次实验不同算法的收敛情况。结合图2可知，IIGA在仅迭代了120次就迅速达到了最优解，而IGA则需要迭代1 417次才能触及这一目标，而GA的收敛过程更为漫长，迭代超过4 000次后才逐渐逼近并最终出现最优解。这一对比证实IIGA在收敛性能方面具有显著优势。

4" 结束语

对于空箱调运问题，针对传统IGA在求解效率与性能方面的不足，提出基于Hamming距离计算公式优化调整的IIGA。通过对兰州铁路局下辖的各集装箱办理站实际运输数据进行实验，并与传统IGA及GA进行对比分析，得出以下结论：（1）通过对Hamming距离计算公式的优化调整，IIGA在抗体亲和度与抗体浓度的度量上实现了更为精确的计算，进而提升了算法在全局搜索与局部优化之间的平衡能力。这种优化使其在求解空箱调运问题时能够表现出更强的适应性。（2）相较于IGA和GA，IIGA在求解铁路空箱调运问题时展现出更为显著的效率与性能。具体而言，IIGA能够在较少的迭代次数内迅速达到最优解，从而有效降低计算成本和时间消耗。（3）实验结果表明，IIGA算法在仿真耗时方面也具有一定的优势。尽管在某些情况下，GA的仿真耗时可能较短，但其收敛速度较慢。相比之下，IIGA算法在保持较快收敛速度的同时，也实现了相对较短的仿真耗时，从而在实际应用中更具竞争力。

" 综上所述，IIGA为空箱调运问题的优化提供了一种更为有效的算法选择。该算法不仅提高了求解效率与性能，还为铁路集装箱运输的整体效益提升提供了有力支持。未来将进一步研究该算法在更大规模空箱调运问题中的应用效果，并探索与其他优化算法的结合使用，以期获得更加高效的求解性能。

参考文献：

[1] 孙浩. 海陆多式联运空箱调运模型研究[J]. 武汉理工大学学报（交通科学与工程版），2010，34（3）：533-536，541.

[2] 邬开俊，鲁怀伟，王铁君. 基于自适应变异粒子群算法的铁路空车调配[J]. 兰州理工大学学报，2011，37（2）：102-105.

[3] 段刚，张慧，陈莉，等. 铁路集装箱空箱调运问题的遗传算法[J]. 铁道科学与工程学报，2011，8（3）：110-115.

[4]" HUANG CHUNHUI. The optimization of empty shipping container reposition based on the network simplex method[C] // International Conference on Management and Service Science， 2011.

[5]" MENG QIANG， SHUAIAN WANG. Liner shipping service network design with empty container repositioning[J]. Transportation Research Part E： Logistics and Transportation Review， 2011，47（5）：695-708.

[6] 石红国，高明瑶. 带时间窗约束的集装箱空箱调运随机机会约束模型研究[J]. 铁道运输与经济，2020，42（2）：87-92.

[7] 邢磊. 中欧班列空箱调运优化研究[D]. 大连：大连海事大学，2021.

[8] 姜志永. 不确定环境下铁路特种箱空箱调运优化[D]. 大连：大连海事大学，2022.

[9] 岳彦辰. 多周期内陆集装箱调运与库存优化研究[D]. 北京：北京交通大学，2023.

[10] 朱星龙，汤银英，陈思. 基于集装箱共享的中欧班列空箱调租优化[J]. 铁道科学与工程学报，2020，17（6）：1571-1577.

[11] 胡广红，汤银英，李鳞睿，等. 考虑集装箱共享的中欧班列空箱调运研究[J/OL]. 铁道运输与经济，1-10（2024-10-20）[2024-12-26]. http：//kns.cnki.net/kcms/detail/11.1949.U.20240825.1729.004.html.

[12]" XU XIAOFENG， XINRU HUANG， LIANJU WANG. Empty container repositioning problem using a reinforcement learning framework with multi-weight adaptive reward function[J]. Maritime Policy amp; Management， 2024，2024：1-22.

[13] 钱力. 基于李雅普诺夫优化的铁路集装箱货运站间空箱协同调运研究[J]. 铁道货运，2024，42（5）：46-52.

收稿日期：2024-10-28

基金项目：国家自然科学基金项目（62262037）；甘肃省科技厅软科学项目（23JRZA360）；中国铁路兰州局集团有限公司科技项目（LZJKY2024012-1）

作者简介：缪莉盼（1999—），女，甘肃庆阳人，兰州交通大学交通运输学院硕士研究生，研究方向：铁路集装箱空箱调运；

向万里（1978—），本文通信作者，男，湖南永顺人，兰州交通大学交通运输学院，教授，博士生导师，研究方向：交通运输规划与管理。

引文格式：缪莉盼，张宇峰，水源，等. 基于改进免疫遗传算法的铁路空箱调运优化[J]. 物流科技，2025，48（3）：121-125.