主动变位索网结构体系索力识别方法及FAST工程应用

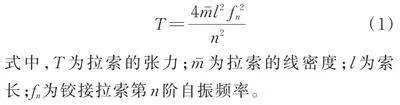
摘要： 为准确识别FAST索网结构体系的拉索索力，本文提出了一种可变弹性边界支承的拉索索力识别方法。建立了拉索等效单自由度模型，推导了理想铰接与弹性边界支承下拉索频率间的数学表达式，通过拉索中点、两端点的第一阶振型值对第一阶频率进行修正，进而提出了基于弦振动理论的主动变位索网结构体系索力识别方法；对单根拉索开展数值仿真，验证了所提方法的准确性，并开展了参数分析；通过数值仿真及现场实测对FAST索网结构进行索力识别，证明了方法的可行性和工程适用性。结果表明：数值仿真的索力识别相对误差在1%以内，现场实测的索力识别相对误差小于5%。该方法考虑了拉索的复杂边界条件，可避免求解未知边界约束刚度，拓展了传统弦振动理论的工程适用性。

关键词： 主动变位索网结构体系； 可变弹性边界支承； 等效单自由度体系； 索力识别； 频率修正

中图分类号： TU394""" 文献标志码： A""""" 文章编号： 1004-4523（2025）01-0135-09

DOI：10.16385/j.cnki.issn.1004-4523.2025.01.015

Cable force identification method of active shape‑changing cable‑net system and its application in FAST engineering

FU Xing¹， SUN Siyuan¹， LI Hongnan¹， LI Qingwei^2，3， LI Hui^2，3， REN Liang¹

（1.School of Infrastructure Engineering， Dalian University of Technology， Dalian 116024， China；2.National Astronomical Observatories， Chinese Academy of Sciences， Beijing 100101， China；3.Key Laboratory of FAST， Chinese Academy of Sciences， Beijing 100101， China）

Abstract： The cable‑net structural system of FAST is a flexible tension cable net， consisting of a main cable net， several hydraulic actuators and controllers， which is the world’s largest span， the highest precision， and the first active shape‑changing cable‑net system. Its characteristic is that the cable net form can be adjusted according to requirements， but it also results in the cable boundary conditions constantly changing with the cable net form， which brings huge challenges to cable force identification. In order to accurately identify cable forces of the active shape‑changing cable‑net system， a method for identifying cable forces of variable elastic boundary supports is proposed. An equivalent single‑degree‑of‑freedom model of the cable is established， and the mathematical expressions of the cable frequencies between ideal hinge and elastic boundary support are derived. The first‑order frequency is then corrected based on the first‑order mode values at the mid‑point and both ends of the cable. The cable force identification method of the active shape‑changing cable‑net system which is based on the string vibration theory is proposed. Numerical simulations are carried out to verify the accuracy of the proposed method， and parametric analyses are also conducted. The method is proved to be practicable and applicable through numerical simulations and field measurements to identify the cable force of the FAST cable net. The results show that the relative errors of cable force identification are within 1% in the numerical simulation and less than 5% in the field measurement. The method takes into account the complex boundary conditions of cables， avoids solving for unknown boundary constraint stiffnesses， and extends the engineering applicability of the traditional string vibration theory.

Keywords： active shape‑changing cable‑net system；variable elastic boundary support；equivalent single‑degree‑of‑freedom system；cable force identification；frequency modification

索网结构具有自重轻、经济性好、易造型等优点，从而被广泛应用于大跨空间结构^［1］。500 m口径球面射电望远镜（Five‑hundred‑meter Aperture Spherical radio Telescope，FAST）是世界上最大的单口径射电望远镜，其反射面采用柔性索网结构体系建造而成。FAST索网结构体系是由主索网、液压促动器、控制器等组成的一种柔性张力索网，是世界上跨度最大、精度最高、第一个采用主动变位工作方式的索网结构体系。反射面形状会根据天体的目标位置实时主动调节，并在观测方向上形成300 m直径的瞬时抛物面，进而实现对未知星体的跟踪观测^［2］。FAST索网结构体系的特点是索网形态可根据需要进行调整，但也导致拉索边界条件随索网形态不断变化，给索力识别带来极大挑战。由于上述功能需求，支撑望远镜的柔性索网结构常常处在持续往复的运动状态下，且大部分索内应力处于较高水平，拉索易产生松弛、疲劳等现象。因此，准确识别FAST拉索索力对整体索网结构的状态控制、安全评估等具有重要意义。

目前，国内外实际工程中主要采用液压千斤顶法（油压表法）、压力传感器法、磁通量法、振动法等测量拉索索力^［3］，前三种索力测量方法仅适用于结构施工阶段，在工程应用中受到较大限制；而振动法在结构施工或建成后均可采用，具有仪器安装简单、便于携带、可重复使用、能实现在线监测等优点，应用非常广泛。振动法识别索力的关键在于准确识别拉索频率和确定频率与索力的关系，现有的模态参数识别方法^［4‑6］完全可以满足频率识别的精度要求。因此，振动法测量索力主要取决于如何精准地确定频率与索力的关系。此关系在两端铰接的理想条件下可按照弦振动或梁振动理论推导，但是在实际工程中，拉索的边界条件通常不是理想铰接，而是介于固接与铰接之间，甚至可能是更加复杂且约束刚度未知的弹性边界条件，导致无法得出拉索频率与索力的显式关系。

针对这一问题，许多学者进行了大量研究工作。黄侨等^［7］考虑拉索端部减振装置弹簧刚度对边界条件的影响，基于弦振动理论提出了二次等效索长修正公式，结合有限元软件ANSYS开展的数值模拟及斜拉桥实测，验证了此方法的正确性和适用性。何伟等^［8］在弹性支承、减振装置、附加质量等复杂边界条件下推导了索力与振动频率的隐式解析表达式，给出了拉索参数和边界条件参数的确定方法，采用郑州黄河二桥工程实例验证了计算公式的准确性。LI等^［9］根据梁振动理论提出了一种短粗索拉力计算方法，考虑了弯曲刚度的影响，取有效振动长度代替原始索长求解索力，通过至少5个传感器实现了索力的动态测量。YAN等^［10］建立了两端受转动弹簧约束的拉索模型，通过求解拉索振型零幅点和建立等效节段模型提出了一种计算未知复杂边界条件下拉索索力的方法。FU等^［11］考虑了拉索垂度和抗弯刚度的影响，提出了基于拉索几何参数（长度和直径）的索力计算方法，索力识别相对误差可以控制在10%以内。

上述学者通过替换拉索长度、引入索长修正系数或边界修正系数对索力计算公式进行了改进，还有一些学者通过求解拉索振动方程得到超越方程，进而引入无量纲参数对拉索振动方程拟合出索力计算公式。GEIER等^［12］考虑识别拉索的固有频率、弯曲刚度和边界条件，采用非对称模态拟合拉索理想频率和无量纲弯曲刚度之间的关系，将理想频率代入弦振动理论公式求解索力，通过现场实测表明索力识别的平均相对误差在5%左右。REBECCHI等^［13］利用任意阶振动频率和对应的5个振型值提出了一种未知边界条件下细长梁轴力识别方法，只需已知梁的弯曲刚度和单位质量即可识别未知长度及边界条件下梁的轴向力。DAN等^［14］对隐式拉索频率方程进行数值求解，得到频率与索力的间接计算方法，在此基础上又进行了经验误差修正。李睿等^［15］根据梁运动方程推导出两端固结拉索的频率方程，用粒子群算法对此超越方程在多维空间中搜索求解，实现了基于两阶实测频率的索力识别。LIU等^［16］分析了拉索模态振型特征，基于随机子空间法和曲线拟合法提出了未知边界条件与抗弯刚度下短索索力的识别方法。YU^［17］基于多模态频率提出一种双频索力计算公式，无需考虑拉索抗弯刚度，任意选择两阶模态频率即可精确计算索力。ZHANG等^［18］选取一段短索计算初始索力，得出考虑垂度、抗弯刚度及边界条件的拉索索力的解析解，再将初始索力作为已知参数更新整个拉索模型，从而计算拉索拉力。XU等^［19］采用高效递归的幅度相位估计方法从实时振动信号中提取时变的振动频率，再对索力和自振频率的关系进行拟合，最终提出了一种时变索力的智能识别方法。

综合上述文献，可以发现现有的研究工作多是对拉索的某一参数修正或者通过隐式方程拟合频率与索力关系的近似公式。近年来随着对工程结构特殊功能的迫切需求，从常见的静态索网结构衍生出了一些主动变位索网结构^{［20‑21］}，其最大特点是采用主动变位的工作方式，但目前识别此类结构索力的常用方法仍以力传感器、磁通量传感器、应变法为主，关于采用振动法识别可变弹性边界拉索索力方面的研究几乎处于空白阶段。因此，本文提出一种考虑可变弹性边界支承的拉索索力识别方法，与已有索力计算公式不同的是，该方法考虑了主动变位索网复杂的边界效应，无需求解边界约束刚度即可识别索力。本文第1节基于弦振动理论和等效单自由度体系推导了适用于主动变位索网结构体系的索力识别方法；第2节通过对单根拉索的数值模拟证明了所提方法的准确性和有效性，探讨了两端边界约束刚度相等和不相等情况下的索力识别精度，开展了参数分析。第3节将所提方法应用于FAST实际工程，对FAST索网进行数值模拟与现场实测，验证了该方法的可行性和工程适用性。第4节总结了本文主要的研究工作，阐明了所提方法的应用前景。

1 可变弹性边界支承的拉索索力识别方法

针对主动变位索网结构体系的工作特点，本文提出了一种考虑可变弹性边界支承的拉索索力识别方法。

1.1 建立索网拉索简化模型

两端铰接拉索在平衡状态下做微幅振动，根据其平面内横向自由振动方程及边界条件^{［22‑23］}，忽略拉索抗弯刚度的影响，可求得拉索索力计算公式为：

（1）

式中，T为拉索的张力；为拉索的线密度；l为索长；f_n为铰接拉索第n阶自振频率。

与铰接拉索不同的是，索网结构的拉索通常以节点盘形式相连接，拉索边界条件为弹性支承，且只有平动刚度，转动刚度很小、可忽略，平动刚度又可随着索网结构形状的变化而变化。故将索网中拉索的边界条件简化为两端轴向支承和竖向支承的弹簧，简化力学模型如图1所示，两端竖向约束弹簧的刚度分别为k₁、k₂；轴向约束弹簧的刚度分别为k₃、k₄。

1.2 等效单自由度体系

两端铰接拉索的第一阶理论振型可表示为，则其第一阶振型的广义质量为：

（2）

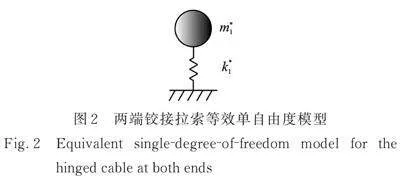
将两端铰接拉索简化为单自由度模型，如图2所示，根据单自由度体系基本振动特性可得：

（3）

式中，ω₁为铰接拉索第一阶自振圆频率；为铰接拉索等效单自由度体系的广义刚度；f₁为铰接拉索第一阶自振频率。

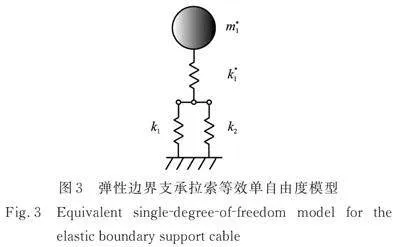
同理，将弹性边界支承拉索等效为单自由度模型：在受到人工或环境激励后，弹性支承拉索在竖向平面内做微幅自由振动，则两端轴向弹簧支承对拉索的第一阶自振频率几乎没有影响，这一结论将在后文单根拉索的数值模拟中进一步得到验证。因而可将拉索等效为如图3所示的单自由度模型。

弹性边界支承拉索的第一阶振型可看作铰接拉索第一阶振型与竖向约束弹簧振型的叠加，如图4所示，其振型由下式计算：

（4）

（5）

（6）

式中，x为沿拉索长度方向的横坐标；代表铰接拉索第一阶振型的最大数值；，分别代表弹性边界支承拉索两端点的第一阶振型值；代表弹性边界支承拉索中点的第一阶振型值。，，均已做归一化处理。

进而可求得弹性边界支承拉索第一阶振型的广义质量为：

（7）

式中，系数a，b可通过模态识别方法获取拉索两端点的振型值，进而通过式（5）求得。

1.3 求解单自由度模型广义刚度

当荷载q沿跨度均匀分布时，即可推导出两端支座等高时拉索的抛物线方程，进而可求得拉索水平张力H。假设索力T与水平张力H的夹角为，如图5所示，则二者关系为。对于索网拉索而言，跨中弧垂通常为10^-2 m数量级，而索长可达数米，甚至数十米，故cosθ≈1，即H≈T。因而可知：

（8）

式中，z为拉索跨中弧垂，即为两端铰接拉索的最大位移。

由于弹性边界支承拉索时刻处于某一受力平衡状态，故荷载ql等于两端竖向支承弹簧的约束反力。由式（8）改写成荷载表达式，得到以下受力平衡关系：

（9）

设一竖向荷载F作用在单自由度模型的质量点上，拉索简化为单自由度模型后产生的位移为，竖向约束弹簧的位移分别为和，则根据受力平衡及胡克定律可推导两端竖向支承弹簧的刚度比为：

（10）

弹性边界支承拉索等效单自由度模型在荷载F作用下的位移为铰接拉索位移与两端约束弹簧的位移之和，即；图3中两竖向支承弹簧k₁和k₂并联，又与铰接拉索单自由度体系的弹簧串联形成综合弹簧，结合式（9）和（10），综合弹簧的刚度可由下式计算：

（11）

定义弹性边界支承拉索的第一阶自振频率为，第一阶自振圆频率为，上述振动特性参数的关系如下所示：

（12）

联立式（11）和（12），得到下式：

（13）

通过式（9）可知，代入式（13）得到两端铰接拉索的广义刚度为：

（14）

1.4 通过振型修正频率

经式（2）计算两端铰接拉索第一阶振型的广义质量为，再通过式（3）求得两端铰接拉索第一阶频率f₁为：

（15）

通过上述理论推导，将弹性边界支承拉索的第一阶自振频率转换为两端铰接拉索的频率f₁，再代入弦振动理论公式中，整理后得到索力计算公式如下：

（16）

由于拉索按照式（4）所示振型振动，各质点之间的位移比值与振型值的比值相等，即，故整理式（16）后索力T可由下式计算：

（17）

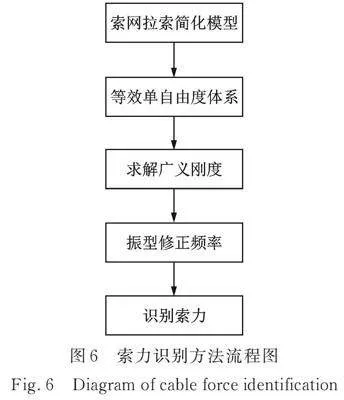
所提方法的理论推导流程如图6所示。在识别索力时，若已知待测拉索的线密度、长度等基本参数，无需其他数据，仅在拉索跨中、两端各安装一加速度传感器（3个测点），拾取的加速度信号经模态识别算法^{［24‑26］}处理，识别出弹性边界支承拉索的第一阶自振频率和跨中、两端共三点的相对振型值，再对其进行归一化处理即可得到对应的振型值、和，进一步求出弹性边界支承拉索第一阶振型的广义质量，代入式（17）即可求解索力大小。即使在索网主动变位后结构形态发生变化，所提方法仍能通过当前结构状态下的加速度数据获取相应模态参数，进而得到新形态下的索力识别结果。

2 单根拉索数值仿真验证

为验证提出方法的准确性，本章建立了单根弹性边界支承拉索的有限元模型，并采用提出的索力识别算法得到不同工况下拉索索力识别结果。

2.1 有限元模型

在ANSYS有限元软件中，采用link180单元模拟拉索，采用combin14单元模拟竖向支承弹簧。此外，根据不同的索力工况，迭代求解拉索实际线形。

本节拉索模型的基本参数如下：直径为0.025"m，全长l为12.39 m，截面积A为3.39×10^-4"m²，线密度为2.89 kg/m，弹性模量为E=2.19×10¹¹ Pa，额定拉断力为726.80 kN。定义左端竖向弹簧刚度与拉索线刚度比为，即；左右两端竖向弹簧的刚度比为，即；令两端轴向弹簧刚度k₃，k₄相等，其与拉索线刚度比为，即。

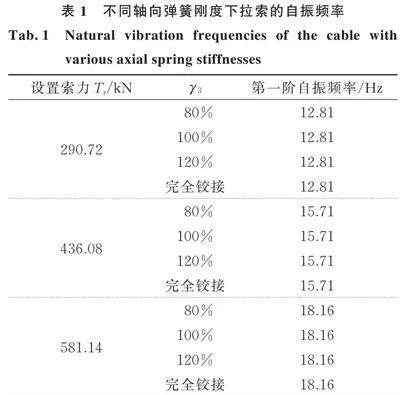
由此建立弹性边界支承拉索的有限元模型，通过改变拉索的索力和轴向支承弹簧刚度建立不同参数的仿真模型，进而开展模态分析，得到如表1所示的自振频率数据。可以看出，不论轴向弹簧刚度如何变化，第一阶自振频率均保持不变，验证了轴向支承弹簧刚度对拉索第一阶自振频率没有影响的结论。

通过改变拉索索力和竖向弹簧支承的刚度模拟不同工况，再施加初始荷载后释放，使拉索在竖向平面内做自由振动，获取拉索跨中、两端点的加速度。整理3个测点的加速度数据，用模态识别算法得到第一阶自振频率和对应振型数值，根据提出的索力识别算法计算索力值。

2.2 索力识别结果

本节以拉索索力为436.08 kN、边界约束刚度k₁为拉索线刚度的0.25倍这一工况为例，进行一次完整的索力识别。

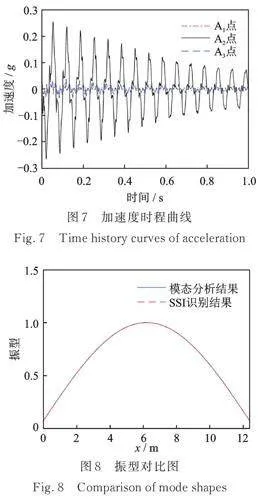
测点的加速度时程曲线如图7所示，其中A₂测点为拉索中点，A₁和A₃测点为拉索两端点（位置对称），故二者时程曲线完全重合。采用SSI算法处理加速度数据，可知弹性边界支承拉索的第一阶自振频率=15.01 Hz，A₁、A₃点振型值为0.0279，A₂点振型值为0.3974。该工况下拉索有限元模型的模态分析结果为：第一阶自振频率为15.0055 Hz，A₁、A₃点振型值为0.0163，A₂点振型值为0.2316。对上述振型值归一化处理，经模态识别算法得到的振型值与模态分析结果基本一致，即铰接拉索振型值=0.9298，竖向支承弹簧振型值==0.0702，拉索振型如图8所示。可以看出，绘制的振型曲线基本重合，说明模态识别算法能够准确地识别拉索第一阶自振频率及对应振型数值。

按照本文提出索力识别方法，由式（12）计算得到弹性边界支承拉索的第一阶自振圆频率=94.31"rad/s；由SSI算法得到的振型值（归一化后）经式（7）计算弹性边界支承拉索的广义质量=18.66 kg，由式（14）解得铰接拉索的广义刚度（含未知索力T），再用式（2）计算铰接拉索第一阶振型的广义质量=17.93 kg，最后通过式（17）计算索力T=436.34 kN。而此工况设置索力为436.08 kN，相对误差仅为0.06%。

2.3 参数分析

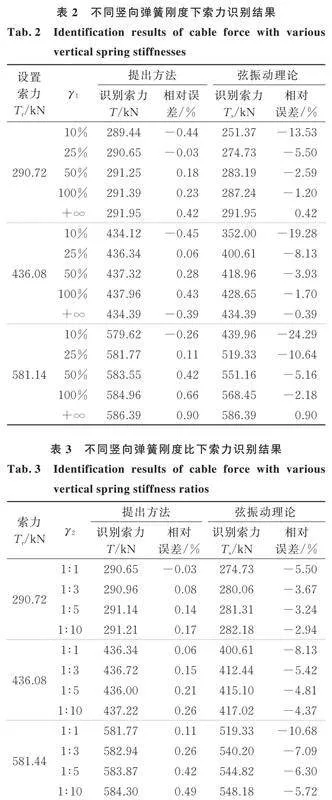
对于两端边界刚度相等的弹性边界支承拉索，竖向支承弹簧刚度（k₁=k₂）分别取拉索线刚度的0.1倍、0.25倍、0.5倍、1倍及+∞（完全铰接），拉力等级分别取拉索额定拉断力的20%、40%、60%、80%和100%。采用本文提出的方法和传统弦振动理论分别计算索力，部分工况的索力识别结果如表2所示。从表2中可知，对于两端边界刚度相等的弹性边界支承拉索，采用本文提出的索力识别方法能得到较为精确的索力值，相对误差在1%以内；而直接采用弦振动理论计算索力，其误差是本文方法的数倍，最大可达24.29%，此时传统弦振动方法已失真。当拉索两端为理想铰接约束时，本文提出方法与传统弦振动理论一致，索力识别相对误差完全相等。

对于两端边界刚度不相等的弹性边界支承拉索，边界刚度与的比值分别取1∶1、1∶3、1∶5和1∶10，索力工况与表2相同，索力识别结果如表3所示。可以看出，当两端竖向弹簧刚度比值越小，索力识别算法的误差越大，但均小于0.5%，而弦振动理论的识别误差仍为本文提出方法的数十倍，故本文提出的索力识别算法比传统的弦振动理论具有更高的精度和更广的适用范围。

3 FAST工程应用

FAST射电望远镜在进行天文观测时，通过控制节点盘、自适应连接机构等主动实现适应性变位，其支撑结构的拉索易产生疲劳、松弛等现象，因此准确识别FAST拉索索力对索网结构状态的控制及运行维护具有重要作用。下面从有限元模拟和现场实测两个角度验证提出方法的工程适用性及精度。

3.1 索网结构数值模拟

在ANSYS有限元软件中建立FAST主索网基准态数值模型，如图9所示，其中主索共6670根，150根边缘主索与圈梁相连，每根主索节点设置连接一根下拉索，共2225根^［27］，图中为部分拉索编号。

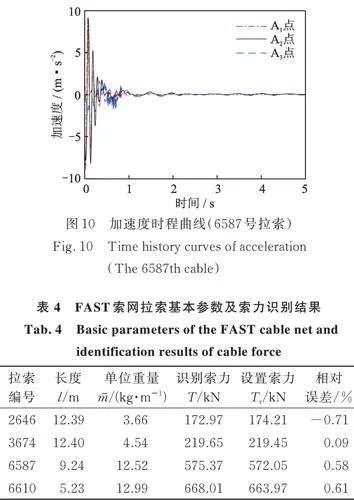
对FAST索网4根拉索施加初始荷载后释放，模拟自由振动，获取拉索两端点（A₁和A₃）和中点（A₂）的加速度响应，部分拉索的加速度时程如图10所示。通过模态识别算法识别拉索的第一阶自振频率和对应的振型值，按照提出的索力识别方法计算索力，结果如表4所示。从表4中可以看出，识别的索力数值与设置索力非常接近，相对误差均小于1%，表明本文提出的索力识别算法具有很高的辨识精度，同时可以适用实际工程结构的复杂约束效应。

3.2 索网结构现场实测

为进一步验证提出方法的工程适用性，在FAST望远镜运维检修时，从中挑选了四根边缘拉索。在拉索跨中和两端索头处共安装3个加速度测点，无线压电式加速度传感器以磁力座吸附方式固定在拉索上，再用胶带对传感器进行加固，采用传感器配套的数据采集系统实现对加速度信号的实时采集和存储，设置采样率为200 Hz。此外，待测拉索在FAST索网建造时已安装磁通量索力传感器，但只能在运维检修时测量索力，此处将其作为索力参考值。传感器布置如图11所示。

两类传感器在环境激励下同时进行数据采集，部分拉索加速度时程如图12所示。采用提出的索力识别方法和弦振动理论分别计算索力，结果如表5所示。以磁通量传感器索力测量结果为基准，可以看出所提索力识别方法与磁通量传感器测量结果的相对误差最大为4.93%，小于5%，而传统弦振动理论的计算误差高达62.61%。这主要是因为传统弦振动理论直接采用识别的拉索频率求解索力，没有考虑边界复杂约束的特点，而本文所提方法考虑了复杂边界效应的影响，通过第一阶振型值对拾取的第一阶自振频率进行修正，因此索力识别结果更准确。值得注意的是，磁通量传感器非常依赖于实验室标定参数，在现场实测中也会存在一定误差，表5中计算的相对误差不代表提出方法的实际误差，但也可看出本文方法与磁通量传感器索力测量结果较为一致，说明本文提出方法满足工程测量精度要求，可以应用于实际工程中。

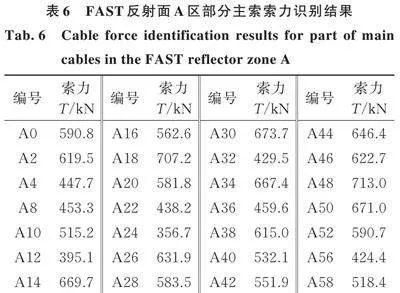
通过上述的索力识别对比结果可以证明本文所提方法能够满足工程上对于索力测量精度的要求，因此在FAST反射面A区部分主索安装了相应数量的光纤光栅加速度传感器及数据采集设备，运用MATLAB软件将提出方法编制成索力在线监测系统，从而实现远端在线观测索网拉索索力。表6为2022年12月4日13时43分的索力识别结果，这里需要说明的是，因索力识别时FAST射电望远镜处于观测阶段，需要良好的电磁环境，导致拉索上原有的磁通量索力传感器无法工作；而光纤光栅加速度传感器及相关设备可以正常工作，不会影响望远镜的正常工作，此处并未给出二者的对比结果。

4 结" 论

本文分析了主动变位索网结构体系中拉索复杂的边界条件，提出了一种可变弹性边界支承拉索的索力识别方法，适用于边界刚度未知或结构形态时变的索网结构体系。该方法仅需已知拉索基本参数和拉索3个测点的振动数据就可准确反演拉索索力。同时通过有限元数值仿真及现场实测对该方法的精度和工程适用性进行了验证。具体结论如下：

（1）本文提出的索力识别方法能得到较为精确的索力值，数值模拟的相对误差在1%以内；直接采用弦振动理论计算索力，其误差是本文方法的数倍以上，误差最大可达24.29%，说明此时传统弦振动方法已失真。

（2）两端竖向弹簧刚度比值越小，索力识别算法的误差越大，但均小于0.5%，说明本文提出的索力识别算法的适用范围较广。

（3）FAST现场实测的索力结果与磁通量传感器测量结果非常接近，两者相对误差小于5%，说明提出方法满足工程上测量精度的要求。

参考文献：

［1］""""""" 沈世钊， 徐崇宝， 赵臣. 悬索结构设计［M］. 北京： 中国建筑工业出版社， 1997.

SHEN Shizhao， XU Chongbao， ZHAO Chen. Design of Cable Structures［M］. Beijing： China Architecture amp; Building Press， 1997.

［2］""""""" 钱宏亮， 范峰， 沈世钊， 等. FAST反射面支承结构整体索网方案研究［J］. 土木工程学报， 2005， 38（12）： 18‑23.

QIAN Hongliang， FAN Feng， SHEN Shizhao， et al. The cable‑net structure supporting the reflector of FAST［J］. China Civil Engineering Journal， 2005， 38（12）： 18‑23.

［3］""""""" ZHANG L X， QIU G Y， CHEN Z S. Structural health monitoring methods of cables in cable‑stayed bridge： a review［J］. Measurement， 2021， 168： 108343.

［4］""""""" ZHANG M J， XU F Y. Variational mode decomposition based modal parameter identification in civil engineering［J］. Frontiers of Structural and Civil Engineering， 2019， 13（5）： 1082‑1094.

［5］""""""" 万熹， 黄天立， 陈华鹏. 环境激励下基于改进经验小波变换的土木工程结构模态参数识别［J］. 振动工程学报， 2020， 33（2）： 219‑230.

WAN Xi， HUANG Tianli， CHEN Huapeng. Improved empirical wavelet transform for modal parameters identification of civil engineering structures under ambient excitations［J］. Journal of Vibration Engineering， 2020， 33（2）： 219‑230.

［6］""""""" 陈永高， 钟振宇. 桥梁结构模态参数识别中系统阶次的自动辨识算法［J］. 振动工程学报， 2021， 34（4）： 680‑689.

CHEN Yonggao， ZHONG Zhenyu. Automatic identification algorithm of system order in modal parameter identification for bridge structures［J］. Journal of Vibration Engineering， 2021， 34（4）： 680‑689.

［7］""""""" 黄侨，胡健琛，黄志伟， 等.考虑减振装置弹簧刚度的斜拉索等效索长及索力测量［J］.东南大学学报（自然科学版）， 2012， 42（4）：724‑728.

HUANG Qiao， HU Jianchen， HUANG Zhiwei， et al. Equivalent length of stayed‑cable considering spring stiffness of damping device and measurement of cable‑force［J］. Journal of Southeast University （Natural Science Edition）， 2012， 42（4）： 724‑728.

［8］""""""" 何伟， 陈淮， 王博， 等. 复杂边界条件下基于频率法的吊杆张力测定研究［J］. 土木工程学报， 2012， 45（3）： 93‑98.

HE Wei， CHEN Huai， WANG Bo， et al. Study of suspender tension measurement based on frequency method with complex boundary conditions［J］. China Civil Engineering Journal， 2012， 45（3）： 93‑98.

［9］""""""" LI S Z， REYNDERS E， MAES K， et al. Vibration‑based estimation of axial force for a beam member with uncertain boundary conditions［J］. Journal of Sound and Vibration， 2013， 332（4）： 795‑806.

［10］""""" YAN B， YU J， SOLIMAN M. Estimation of cable tension force independent of complex boundary conditions［J］. Journal of Engineering Mechanics， 2015， 141（1）： 06014015.

［11］""""" FU Z Q， JI B H， WANG Q D， et al. Cable force calculation using vibration frequency methods based on cable geometric parameters［J］. Journal of Performance of Constructed Facilities， 2017， 31（4）： 04017021.

［12］""""" GEIER R， DEROECK G， FLESCH R. Accurate cable force determination using ambient vibration measurements［J］. Structure and Infrastructure Engineering， 2006， 2（1）： 43‑52.

［13］""""" REBECCHI G， TULLINI N， LAUDIERO F. Estimate of the axial force in slender beams with unknown boundary conditions using one flexural mode shape［J］. Journal of Sound and Vibration， 2013， 332（18）： 4122‑4135.

［14］""""" DAN D H， CHEN Y Y， YAN X F. Determination of cable force based on the corrected numerical solution of cable vibration frequency equations［J］. Structural Engineering and Mechanics， 2014， 50（1）： 37‑52.

［15］""""" 李睿， 李晓章， 郑祥隆， 等. 粒子群算法在基于频率的两端固结吊杆索力识别中的应用［J］. 振动与冲击， 2018， 37（9）： 196‑201.

LI Rui， LI Xiaozhang， ZHENG Xianglong， et al. Application of PSO in frequency‑based tension identification of hanger rods with two fixed ends［J］. Journal of Vibration and Shock， 2018， 37（9）： 196‑201.

［16］""""" LIU C， ZHENG W. An estimation method of short cable force based on modal identification［J］. Journal of Highway and Transportation Research and Development， 2020， 37（1）： 74‑84.

［17］""""" YU C P. Tension prediction for straight cables based on effective vibration length with a two‑frequency approach［J］. Engineering Structures， 2020， 222： 111121.

［18］""""" ZHANG S H， SHEN R L， WANG Y， et al. A two‑step methodology for cable force identification［J］. Journal of Sound and Vibration， 2020， 472： 115201.

［19］""""" XU B， DAN D， YU X. Real‑time online intelligent perception of time‑varying cable force based on vibration monitoring［J］. Engineering Structures， 2022， 270： 114925.

［20］""""" 陆金钰，鲁梦.蚁群算法在自适应索穹顶结构内力控制中的应用［J］. 东南大学学报（自然科学版）， 2017， 47（6）： 1161‑1166.

LU Jinyu， LU Meng. Application of ant colony algorithm in internal force control of adaptive cable dome［J］. Journal of Southeast University （Natural Science Edition）， 2017， 47（6）： 1161‑1166.

［21］""""" CHEN D S， ZHANG Y， QIAN H L， et al. An effective form analysis approach for designing and optimizing a cable‑net structure of a giant active reflector［J］. Aerospace， 2021， 8（9）： 269.

［22］""""" IRVINE H M. Cable" Structures［M］. Cambridge： The" MIT" Press， 1981.

［23］""""" ZUI H， SHINKE T， NAMITA Y. Practical formulas for estimation of cable tension by vibration method［J］. Journal of Structural Engineering， 1996， 122（6）： 651‑656.

［24］""""" LI W C， VU V H， LIU Z H， et al. Extraction of modal parameters for identification of time‑varying systems using data‑driven stochastic subspace identification［J］. Journal of Vibration and Control， 2018， 24（20）： 4781‑4796.

［25］""""" REYNDERS E P B. Uncertainty quantification in data‑driven stochastic subspace identification［J］. Mechanical Systems and Signal Processing， 2021， 151： 107338.

［26］""""" ZHOU K， LI Q S， HAN X L. Modal identification of civil structures via stochastic subspace algorithm with monte carlo‑based stabilization diagram［J］. Journal of Structural Engineering， 2022， 148（6）： 04022066.

［27］""""" 朱忠义， 张琳， 王哲， 等. 500 m口径球面射电望远镜索网结构形态和受力分析［J］. 建筑结构学报， 2021， 42（1）： 18‑29.

ZHU Zhongyi， ZHANG Lin， WANG Zhe， et al. Form‑finding and structural behavior of cable net of Five‑hundred‑meter Aperture Spherical radio Telescope［J］. Journal of Building Structures， 2021， 42（1）： 18‑29.

通信作者： 付" 兴（1988—），男，博士，副教授。E‑mail： fuxing@dlut.edu.cn

基金项目："国家自然科学基金资助项目（52027811，11973006）