基于递归本征正交分解与强跟踪扩展卡尔曼滤波的结构损伤识别

摘要： 针对目前已有损伤识别方法难以实时跟踪结构损伤且计算量大的问题，提出了一种基于递归本征正交分解（recursive proper orthogonal decomposition， RPOD）与强跟踪扩展卡尔曼滤波（strong tracking extended Kalman filter， STEKF）相结合的模型降阶与结构损伤在线识别方法，对动载荷作用下的结构损伤识别进行了研究。利用RPOD方法在线更新并实时建立反映结构状态的降阶模型，解决未知载荷作用下多自由度结构动力分析计算量大且难以收敛的问题，同时跟踪损伤的演化并对其进行定位；通过STEKF方法跟踪降阶模型的状态向量，识别因损伤而退化的降阶模型参数。分别采用六层剪切型框架的数值模拟与三层钢框架的模型试验验证了该方法的可行性，结果表明，所提出的方法能够准确建立降阶模型并跟踪降阶模型参数的时变历程，同时可以有效地识别出剪切型建筑结构损伤的位置和程度，即使在处理高程度噪声时仍有较高的精度。

关键词： 损伤识别； 模型降阶； 递归本征正交分解； 强跟踪扩展卡尔曼滤波； 数据驱动

中图分类号： TU3111.3； TB122""" 文献标志码： A""" 文章编号： 1004-4523（2025）01-0117-09

DOI：10.16385/j.cnki.issn.1004-4523.2025.01.013

Structural damage identification based on recursive proper orthogonal decomposition and strong tracking extended Kalman filtering

Yang Shaochong^1，2， Yao Yuan^1，2， Liu Jialiang^1，2， Lei Zhen^1，2， Fang Youliang^1，2

（1.College of Civil Engineering and Architecture， Hebei University， Baoding 071002， China；2.Technology Innovation Center for Testing and Evaluation in Civil Engineering of Hebei Province， Baoding 071002， China）

Abstract： Aiming at the problem that the existing damage identification methods are difficult to track the structural damage in real time and require a large amount of calculation， a model order reduction and online damage identification method based on the combination of recursive proper orthogonal decomposition （RPOD） and strong tracking extended Kalman filter （STEKF） is proposed. The structural damage identification under dynamic load is studied. The RPOD method is used to update online and construct the reduced-order model reflecting the structure state in real time， which solves the problem of large calculation and difficult convergence of dynamic analysis of multi-degree of freedom structures under unknown loads. Meanwhile， the evolution of damage is tracked and located. The STEKF method is used to track the state vector of the reduced-order model and identify the reduced-order model parameters degraded by damage. The feasibility of the proposed method is verified by numerical simulation of a six-story shear frame and model test of a three-story steel frame. The results show that the proposed method can accurately construct the reduced-order model and track the time-varying history of the reduced-order model parameters. Meanwhile， it can effectively identify the location and extent of the damage of the shear building structure， even when dealing with high levels of noise， it retains high accuracy.

Keywords： damage identification；reduced-order modeling；recursive proper orthogonal decomposition （RPOD）；strong tracking extended Kalman filter （STEKF）；data driven

由于各种力学和环境因素的影响，土木工程结构在服役期间易产生不同程度的损伤，损伤的不断累积会导致结构出现局部破坏或失效。结构健康监测（structural health monitoring， SHM）可以通过各类传感设备获取结构响应，实现对结构的长期监测^［1⁃2］，其中结构振动损伤识别技术是SHM领域的重要研究方向之一，近年来也取得了丰富的成果^［3⁃5］。然而，实际工程结构往往维数较高，目前的损伤识别方法在求解时计算量会成倍增加，难以实时、快速地对损伤进行识别，从已有文献看，用于土木工程领域的在线损伤识别方法有着较大的进步空间。

目前的损伤识别方法大多以检测结构的力学性能为主要目标，而结构力学性能的降低往往被认为是系统中某一参数因损伤的出现而发生退化的结果^［6］，因此对结构损伤的检测可以看作是系统参数识别问题。针对目前参数识别问题中建模和数据测量的不确定性，通常采用卡尔曼滤波（Kalman filter， KF）对结构的物理参数进行在线估计。KF是一类以最小均方差为准则的状态最优估计法，根据实时响应信号对识别结果进行修正，能够对系统下一步走向做出有根据的预测。雷鹰等^［7］将KF与子结构、最小二乘法相结合，对未知载荷作用下结构的参数进行了识别；张肖雄等^［8］针对有限观测信息下的参数识别问题，将KF与递推最小二乘法（RLSE）相结合，实现了对系统响应的有效估计。为了提高识别过程的稳定性与准确性，不少学者开始采用扩展卡尔曼滤波（extended Kalman filter， EKF）对结构参数进行识别。雷鹰等^［9］针对框架结构梁柱单元的损伤问题，将EKF与静力凝聚算法相结合，成功识别出节点损伤的位置和程度。PAN等^［10］提出了载荷未知情况下的EKF方法，优先对已知载荷位置的响应进行识别，在此基础上进一步识别未知载荷处的响应。YANG等^［11］对EKF进行扩展，提出自适应EKF法，将自适应矩阵引入状态误差协方差矩阵中，以跟踪时变参数。但利用EKF进行求解时，需要将待识别参数扩展到结构的状态向量中，这会导致计算效率下降，特别是对于大型结构，往往会因维数过高而出现收敛困难、精度降低等问题^［12］。因此，选择一种合适的降阶技术，是将EKF方法应用到土木工程结构损伤识别领域的关键。

本征正交分解（proper orthogonal decomposition， POD）是一类高效的模型降阶技术^［13］，能在减少模型自由度的同时，仅利用结构响应对其主要特征信息进行提取，保证降阶模型具有足够高的精度。近年来，该方法已被广泛应用于模型降阶问题中^［14］，包括航空航天^{［15⁃16］}、计算流体力学^［17］、材料力学^［18］等领域，同时大量研究表明仅利用前两阶本征模态（POMs）便可以跟踪降阶模型的演化^{［19⁃20］}，且效果优于传统降阶方法。除在模型降阶方面有较高的效率和精度外，基于POD方法得到的POMs，可以用于表征结构损伤的位置和程度，GALVANETTO等利用该方法对简支梁分别进行了数值模拟^［21］和模型试验^［22］，仅利用响应数据成功识别出了损伤的程度和位置。WANG等^［23］将POD与粒子群优化算法（PSO）相结合，有效地识别出了剪切型建筑物不同程度的损伤。然而，传统POD方法在计算时需要获取一段时间的响应数据来构造快照矩阵，特别是高维结构，需要大量的内存和运算步骤，因此许多学者开始研究在线POD（online POD）识别损伤。AZAM等^［24］利用POD和递归贝叶斯滤波对结构进行在线损伤识别研究；LU等^［25］对在线POD领域的部分研究进行了整理和总结，阐明了此类方法在损伤识别领域具有较为广阔的发展前景。

本文发展了一种基于递归本征正交分解（recursive proper orthogonal decomposition， RPOD）与强跟踪扩展卡尔曼滤波（strong tracking extended Kalman filter， STEKF）相结合的双重识别方法，对动载荷作用下的结构损伤识别与模型降阶方法进行研究。针对多自由度结构动力分析计算量大且难以求解的问题，利用结构的实时响应构造快照矩阵，通过POD方法提取矩阵中的特征信息，减少结构模型的自由度，构建能够关联能量最优的降阶模型；针对损伤演化情况下降阶模型的更新问题，利用KF在线更新POMs，发展RPOD方法精确跟踪结构动态性能的降阶模型；为实现在线实时跟踪损伤的演化，识别因损伤导致突变的参数，拟引入时变的遗忘因子，发展STEKF方法对降阶模型物理参数进行识别。

1 基于本征正交分解的动态模型降阶

POD是一类基于动态响应数据驱动的模型降阶方法，根据系统动力响应构造快照矩阵，选择一组最能够表征系统特征的POM，以获取结构的主要特征。

当结构受到外部载荷的影响时，其动力响应可用以下运动方程来描述：

（1）

式中，为质量矩阵；为阻尼矩阵；为刚度矩阵；分别为结构位移、速度和加速度响应向量；为随时间变化的外载荷向量。

利用POD方法进行模型降阶时，考虑位移响应向量，其中，为实数的集合，为的维数。对于线性系统，可以表示为如下形式：

（2）

式中，为模态坐标下的位移响应，排列在列向量中；（）为一组标准正交基，称为POMs；为坐标转换矩阵，由所选取的正交基组成，表示为：

（3）

通常，我们仅需要保留前几阶POMs，就可以跟踪系统的演化，可将式（2）简化为：

（4）

在式（4）中，考虑（对于大型结构，）。为收集了矩阵前列（即前阶基底）的矩阵，收集了列向量的前个分量，需要在保证降阶模型精度的前提下保留合适的POMs数量。

首先，需要为向量提供一个子空间，计算个时刻的位移，并将其收集到快照矩阵中：

（5）

对快照矩阵进行奇异值分解，可以得到：

（6）

式中，和分别为和的正交矩阵；为一个的矩阵，其主对角线上的元素称为矩阵的奇异值。

快照矩阵的左奇异向量收集了结构的全部POMs，同时大量研究表明，第个奇异值的平方表示其对应的最大值，即POMs的能量最大值，可通过下式选择满足精度要求的POM数量：

（7）

式中，为精度，当满足时，前阶POMs可以表示原始系统的大部分特征。以式（7）作为准则，选取此时的值作为保留的POM阶数，并将左奇异矩阵的前阶列向量组成降阶POMs。

当利用POD方法获取了所需的最优POMs，位移矢量便可以通过来近似。矩阵是位置向量的函数，同时定义了结构POMs的形状，而矩阵定义了结构响应随时间的演化：

（8）

因此，式（1）可近似为：

（9）

将式（9）两端左乘，得到降阶模型的运动方程为：

（10）

或将其等价为：

（11）

式中，为模态质量矩阵；为模态阻尼矩阵；为模态刚度矩阵；为模态外载荷矩阵。

一旦得到模态坐标下式（11）的解，便可利用式（8）将结构在模态坐标下的位移变换到物理坐标下，得到物理坐标下的位移响应。

对于线弹性结构，一阶POM可以用于表示结构的主要特征并保证降阶模型有足够的精度，同时可以准确地对结构损伤进行识别。本文采用一阶POM构建降阶模型，能够反映结构的损伤情况并减少计算量。

2 基于RPOD⁃STEKF的结构损伤双重识别方法

当结构出现损伤时，对于POD方法构建的降阶模型，具体表现为POMs发生变化。为了保证状态估计能够实时反映结构的损伤，本文基于响应数据，利用RPOD方法对POMs进行在线更新，追踪POMs的演化过程。

具体分析步骤为：首先将式（3）所保留的POMs以向量的形式排列如下：

（12）

式中，表示POMs可以随时间改变；为POM的阶数；为时间步。

考虑到因损伤导致的系统演化，将POMs的演化表示为：

（13）

式中，为零均值的高斯白噪声，上标“”表示POMs更新时的各项参数，需要对其时不变协方差进行调整，以获得POMs和其余待识别模型参数的准确估计。

与传统KF算法相同，式（13）需要一个观测方程来补充，并根据测量值对POMs进行更新，设置观测方程：

（14）

式中，为将POMs和观测方程联系起来的转换矩阵；为观测噪声。

此时，式（13）和（14）构成了POMs演化的状态空间方程。因状态向量呈线性变化，仅需采用KF方法对POMs进行递归更新，在计算前需要定义POMs的初值及其初始协方差。

每一步预测开始前假定POM初值，由于在预测前并不知道结构是否会发生损伤，因此假定POM的初值保持不变，与上一步的预测结果一致。然后进入预测阶段：

（15）

（16）

式中，表示POMs的状态预测误差协方差矩阵。

对卡尔曼增益进行计算：

（17）

式中，表示POM更新时的状态转换矩阵。

对POMs进行更新并对其滤波误差协方差矩阵进行求解：

（18）

（19）

式中，为更新后的状态估计值；为滤波（后验）误差协方差矩阵。

通过对上述公式迭代求解，便可以对结构的POMs进行在线更新，实时构建降阶模型的同时达到识别损伤的目的。

接下来对降阶模型的刚度参数进行识别：本文发展的STEKF方法是在传统EKF方法中引入时变的遗忘因子，以增强滤波过程中新信息的占比。首先需要对降阶模型的状态进行定义，与全阶模型相似，降阶模型的状态方程和观测方程可以分别定义为：

（20）

（21）

式中，上标“”表示降阶模型更新时的各类参数；为降阶模型的状态向量，可以表示为：

（22）

式中，为降阶模型位移向量；为系统的状态转移矩阵；和分别为降阶模型的系统噪声和观测噪声；为观测转移矩阵；为转换矩阵，用以将实际测量结果转换到降阶模型中：

（23）

为解决结构参数的识别问题，将降阶模型的状态和待识别参数统一到降阶模型的状态向量中，并将其表示为：

（24）

式中，表示待识别参数（如刚度、阻尼等）。

此时，利用STEKF表示的状态方程及其观测方程的表达式分别为：

（25）

（26）

由于状态向量中补充了待识别参数，式（23）转换为，用以将观测结果与扩展状态向量相转换。

定义初始状态及其协方差，之后进入预测阶段。首先利用STEKF方法对状态进行预测：

（27）

（28）

式中，为的雅可比矩阵，表示状态转移矩阵；表示状态预测的误差协方差矩阵；为时变的遗忘因子，可以实时对卡尔曼增益的值进行调整，保证滤波对突变参数的跟踪能力。

接下来进入更新阶段，计算卡尔曼增益：

（29）

对状态空间进行更新并求其滤波误差协方差矩阵：

（30）

（31）

式中，为更新后的状态估计值；为滤波（后验）误差协方差矩阵。

具体技术路线如图1所示，基于响应数据组成快照矩阵并提取其特征，利用RPOD算法跟踪POM的演化过程，实现对损伤的准确定位，并构建反映结构实时状况的降阶模型；同时利用STEKF算法识别降阶模型刚度参数突变的时间及大小。

3 数值模拟

3.1 仿真模型

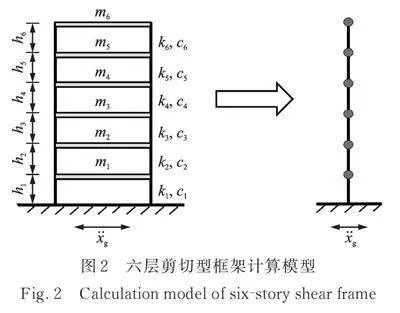
为了验证该方法的可行性，考虑受地震载荷作用的六层剪切型框架，如图2所示。各层质量为：；层间刚度分别为：，，；层间阻尼分别为：，，。地震动选择El‑Centro波，作用于框架底部，峰值加速度，采样时间间隔为，地震载荷作用时间为55 s。将利用法计算得到的位移响应作为观测值，同时为了验证该方法在高水平噪声影响下的有效性，在位移响应中加入了15%的高斯噪声，利用位移响应构造快照矩阵，对其进行POD分解以得到未损伤结构的POMs。

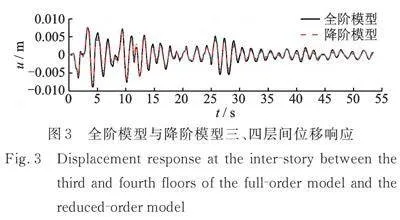
本节通过层间刚度减小来模拟损伤，即，其中，表示损伤程度，表示层数。首先验证降阶模型的准确性：将全阶模型的位移响应与POM构成的降阶模型的位移响应进行对比，结果如图3所示，降阶模型和全阶模型的位移响应一致，说明利用训练所得POM可以准确构建降阶模型。

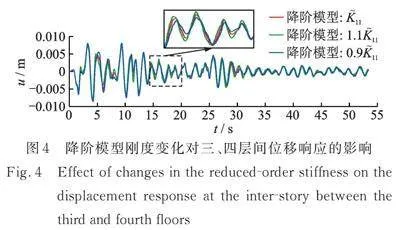
接下来验证降阶模型对刚度参数改变的敏感程度，考虑降阶模型的刚度改变，如图4所示，当发生改变时，降阶模型的位移响应会发生一定程度的变化，说明当降阶模型刚度参数发生改变时，可以通过响应的改变达到损伤识别的目的，即使是微小的损伤，也能作出反应。

3.2 损伤识别结果分析

利用所发展的RPOD⁃STEKF方法对结构损伤进行识别，在进行滤波前需要对POM的初始参数进行设置，初始协方差矩阵，系统噪声协方差矩阵，观测噪声协方差矩阵。

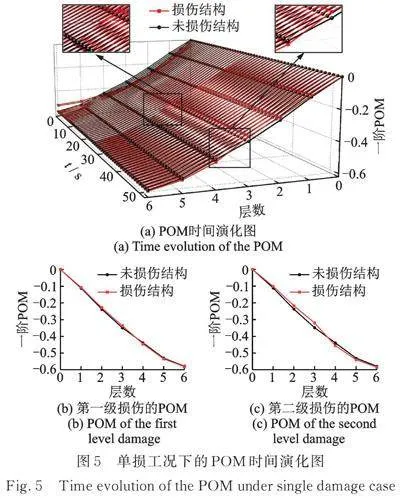
模型选用图2所示的剪切型框架模型，首先考虑单损伤工况，所设置的损伤类型为层间刚度逐级递减：第一级损伤出现时间设置在第8 s，损伤程度为20%，随着时间的推进以及载荷的持续施加，结构可能会发生进一步损伤，设置第二级损伤出现在第24 s，损伤程度为50%，两次损伤位置均位于第三层和第四层之间，利用RPOD方法对POM进行更新，更新结果如图5所示。

图5（a）为高噪声情况下RPOD方法更新得到的损伤与未损伤结构的POM时间演化图，图中红色线代表损伤结构的一阶POM，黑色线代表未损伤结构的一阶POM，可以看出图像前3 s红色线波动较大，这说明在该算法的初始阶段，噪声影响较大，但随着算法的推进，图像逐渐收敛到稳定值，之后在第10 s左右，图像在损伤位置处发生变化。当第二级损伤出现时（第24 s），由于损伤程度的增加，损伤结构的一阶POM图像会在损伤位置出现第二次变化，有效跟踪损伤随时间的演化过程，为了更直观地看到损伤识别结果，图5（b）和（c）分别为图像稳定时各级损伤的POM，可见随着损伤程度的增加，图像在损伤位置处的突变量明显增加，说明该方法可以很好地对不同程度的损伤进行识别。

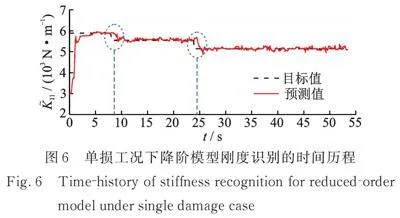
接下来通过训练得到的POM构造随时间变化的降阶模型，并利用STEKF方法对降阶模型的刚度进行识别。首先需要对算法的初始参数进行设置：初始协方差矩阵，系统噪声协方差矩阵，观测噪声协方差矩阵，识别结果如图6所示。在滤波的初始阶段，识别过程会产生较大程度的波动，但会迅速达到稳定，准确地对不同损伤时刻的进行识别，说明当模型出现逐级不同程度的损伤时，利用STEKF方法可以准确地跟踪的时变历程。

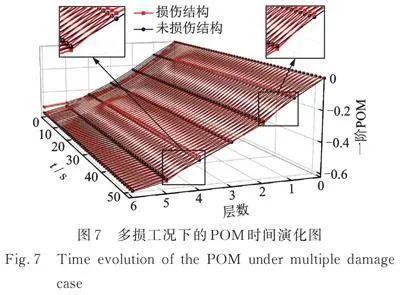
针对多位置损伤工况进行分析，设置第8 s出现损伤，损伤位于第二层和第五层，损伤程度为50%，在结构响应中加入15%的高斯白噪声，利用RPOD算法对其进行识别，结果如图7所示。当出现多处位置损伤时，POM的时间演化曲线会在出现损伤时快速作出改变，代表损伤POM的红色曲线会在损伤位置处发生呈下降趋势的突变，由此可以准确识别出结构的损伤。

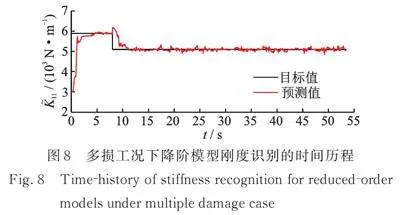
图8为多损工况下对降阶模型的识别结果，可见STEKF方法能够实现对的准确跟踪，同时证明了本方法得到的POM能够实时构建反映结构状态的降阶模型。

4 钢框架模型试验验证

为进一步验证本方法基于实测数据进行损伤识别的有效性，开展了模型试验。

4.1 模型简介

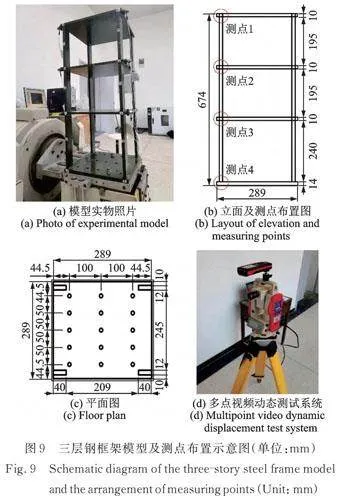
如图9所示，制作的试验模型为三层钢框架，楼板尺寸为289 mm×289 mm，厚度均为10 mm；立柱尺寸为12 mm×40 mm，一、二、三层柱高分别为240、195、195 mm，材料选用牌号为Q235的钢，弹性模量为210 MPa，泊松比为0.273。楼板与立柱连接处通过焊接实现刚性连接，框架结构底部通过螺栓与振动台固定。本试验测点布置在每层楼板的一侧，共布置4个测点，将框架底部的测点作为基准点。

4.2 损伤工况

本试验对三种不同的损伤工况进行了研究，图10（a）～（c）分别为各损伤工况示意图。如图10（d）所示，损伤的引入通过柱子局部开口来实现，各损伤工况设置如表1所示。

如图9（a）和（d）所示，利用DY⁃300⁃3型振动台施加随机载荷，采用多点视频动态位移测试系统获取无损和有损工况下结构的位移响应信号，对于工况1和3而言，0～25 s是无损工况响应信号，25～60 s是损伤工况响应信号；对于工况2而言，25～45 s是第一级损伤工况响应信号，45～60 s是第二级损伤工况响应信号。

4.3 实测信号识别结果

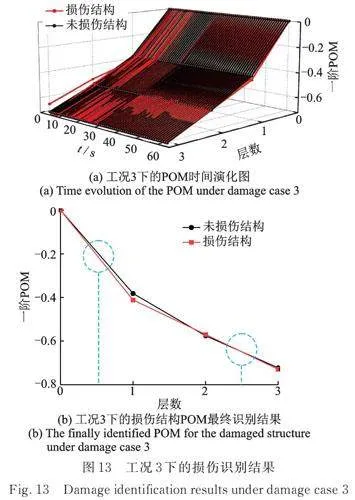
利用本方法对每种工况的损伤进行识别，各工况的识别结果如图11～13所示。

结果表明，本方法可以通过模型试验实测响应数据有效识别框架结构单点和多点的损伤，当代表损伤POM的红色曲线在损伤位置处发生呈下降趋势的突变时，便可快速、准确地对损伤进行定位。相比数值模拟的结果，滤波前期波动较大，但也会在2 s内达到稳定，当出现损伤时（25 s），会快速训练出损伤演化的过程，并在损伤位置出现突变。

图12表示对逐级损伤的分析结果，由图12（a）可见，POM演化图像会在各级损伤出现后产生明显的变化，说明本方法可对损伤后的响应信号快速作出反应，图12（b）为图像稳定时各级损伤的POM，说明本方法可以对不同程度的损伤进行准确识别。

如图13所示，红色曲线在一层突变量大于在三层突变的量级，即在一、三层损伤程度相同的情况下，一层损伤的识别效果明显。

5 结 论

本文发展了基于RPOD与STEKF相结合的双重损伤识别方法，对动力学降阶模型及参数的实时跟踪问题进行了深入研究，该方法可以在计算过程中有效减少计算量，实现在线实时健康监测，在结构出现损伤时作出快速准确地诊断，对推动结构损伤识别实用化发展具有重要意义。主要得到以下结论：

（1）针对降阶模型实时更新问题，发展了RPOD方法，通过时变响应动态跟踪反映结构损伤演化的一阶POM，对降阶模型进行在线更新。通过数值分析和模型试验验证了该方法的准确性，所获取的一阶POM可以动态跟踪损伤的演化并对其进行定位。

（2）针对降阶模型参数识别问题，为解决传统EKF方法难以对时变参数进行识别的问题，在算法中引入了时变的遗忘因子，增大了新的响应数据在计算过程中的占比，保证滤波可以准确跟踪降阶模型的参数变化。研究结果表明，所发展的STEKF方法可以对降阶模型刚度参数突变的时间以及大小进行准确识别。

（3）本方法仅基于环境激励获取的动响应信号特征进行损伤识别，有效解决了外部载荷未知情况下实际工程的健康监测问题。

参考文献：

［1］""""""" BAO Y Q， CHEN Z C， WEI S Y， et al. The state of the art of data science and engineering in structural health monitoring［J］. Engineering， 2019， 5（2）： 234-242.

［2］""""""" 雷鹰， 刘丽君， 郑翥鹏. 结构健康监测若干方法与技术研究进展综述［J］. 厦门大学学报（自然科学版）， 2021， 60（3）： 630-640.

LEI Ying， LIU Lijun， ZHENG Zhupeng. Review on the developments of some methods and techniques in structural health monitoring［J］. Journal of Xiamen University （Natural Science）， 2021， 60（3）： 630-640.

［3］""""""" 缪炳荣， 杨树旺， 王名月， 等. 利用振动响应的多种结构损伤识别方法比较［J］. 振动工程学报， 2020， 33（4）： 724-733.

MIAO Bingrong， YANG Shuwang， WANG Mingyue， et al. Comparison of various structural damage identification methods using vibration response［J］. Journal of Vibration Engineering， 2020， 33（4）： 724-733.

［4］""""""" 李慧民， 董美美， 熊雄， 等. 基于振动的结构损伤识别研究综述［J］. 建筑结构， 2021， 51（4）： 45-50.

LI Huimin， DONG Meimei， XIONG Xiong， et al. State-of-the-art review of vibration-based damage identification framework for structures［J］. Building Structure， 2021， 51（4）： 45-50.

［5］""""""" 赵一男， 公茂盛， 杨游. 结构损伤识别方法研究综述［J］. 世界地震工程， 2020， 36（2）： 73-84.

ZHAO Yinan， GONG Maosheng， YANG You. A review of structural damage identification methods［J］. World Earthquake Engineering， 2020， 36（2）： 73-84.

［6］""""""" YANG J N， LIN S. Identification of parametric variations of structures based on least squares estimation and adaptive tracking technique［J］. Journal of Engineering Mechanics， 2005， 131（3）： 290-298.

［7］""""""" 雷鹰， 毛亦可. 部分观测下基于子结构的大型结构损伤诊断法［J］. 工程力学， 2012， 29（7）： 180-185.

LEI Ying， MAO Yike. A damage detection algorithm based on substructures for large size structures under limited measurements［J］. Engineer Mechanics， 2012， 29（7）： 180-185.

［8］""""""" 张肖雄， 贺佳， 许斌. 基于卡尔曼滤波和递推最小二乘在部分观测信息下的参数识别法［J］. 地震工程与工程振动， 2019， 39（2）： 134-140.

ZHANG Xiaoxiong， HE Jia， XU Bin. Structural parameter identification basing on Kalman filter and recursive least square estimation with limited observations［J］. Earthquake Engineering and Engineering Dynamics， 2019， 39（2）： 134-140.

［9］""""""" 雷鹰， 李青. 基于扩展卡尔曼滤波的框架梁柱节点地震损伤识别［J］. 土木工程学报， 2013， 46（增刊1）： 251-255.

LEI Ying， LI Qing. Damage detection of beam-column joints in frame structures under seismic excitation based on extended Kalman filter［J］. China Civil Engineering Journal， 2013， 46（Sup1）： 251-255.

［10］""""" PAN S W， XIAO D， XING S T， et al. A general extended Kalman filter for simultaneous estimation of system and unknown inputs［J］. Engineering Structures， 2016， 109： 85-98.

［11］""""" YANG J N， PAN S， HUANG H. An adaptive extended Kalman filter for structural damage identifications II： unknown inputs［J］. Structural Control and Health Monitoring， 2007， 14 （3）： 497-521.

［12］""""" 唐宏志， 姜金辉. 扩展卡尔曼滤波对时变参数追踪性能的影响研究［J］. 南京航空航天大学学报， 2022， 54（2）： 304-310.

TANG Hongzhi， JIANG Jinhui. Research on tracking performance of extended Kalman filter for time varying parameters［J］. Journal of Nanjing University of Aeronautics amp; Astronautics， 2022， 54（2）： 304-310.

［13］""""" 路宽， 张亦弛， 靳玉林， 等. 本征正交分解在数据处理中的应用及展望［J］. 动力学与控制学报， 2022， 20（5）： 20-33.

LU Kuan， ZHANG Yichi， JIN Yulin， et al. Application and outlook of proper orthogonal decomposition in data processing［J］. Journal of Dynamics and Control， 2022， 20（5）： 20-33.

［14］""""" RITTO T G， BUEZAS F S， SAMPAIO R. A new measure of efficiency for model reduction： application to a vibroimpact system［J］. Journal of Sound and Vibration， 2011， 330（9）： 1977-1984.

［15］""""" 陈兵， 龚春林， 仇理宽， 等. 基于频域本征正交分解的几何非线性动力学降阶［J］. 振动与冲击， 2020， 39（21）： 163-172.

CHEN Bing， GONG Chunlin， QIN Likuan， et al. Order reduction of geometrically nonlinear dynamic system based on POD in frequency domain［J］. Journal of Vibration and Shock， 2020， 39（21）： 163-172.

［16］""""" 梅冠华， 康灿， 张家忠. 二维壁板颤振的本征正交分解降阶模型研究［J］. 振动与冲击， 2017， 36（23）： 144-151.

MEI Guanhua， KANG Can， ZHANG Jiazhong. Reduced order model based on proper orthogonal decomposition for two-dimensional panel flutter［J］. Journal of Vibration and Shock， 2017， 36（23）： 144-151.

［17］""""" 邱亚松， 白俊强， 华俊. 基于本征正交分解和代理模型的流场预测方法［J］. 航空学报， 2013， 34（6）： 1249-1260.

QIU Yasong， BAI Junqiang， HUA Jun. Flow field estimation method based on proper orthogonal decomposition and surrogate model［J］. Acta Aeronautica et Astronautica Sinica， 2013， 34（6）： 1249-1260.

［18］""""" XIE D， XU M， DAI H H， et al. Proper orthogonal decomposition method for analysis of nonlinear panel flutter with thermal effects in supersonic flow［J］. Journal of Sound and Vibration， 2015， 337： 263-283.

［19］""""" LU K， YU H， CHEN Y S， et al. A modified nonlinear POD method for order reduction based on transient time series［J］. Nonlinear Dynamics， 2015， 79（2）： 1195-1206.

［20］""""" LU K， JIN Y L， CHEN Y S， et al. Stability analysis of reduced rotor pedestal looseness fault model［J］. Nonlinear Dynamics， 2015， 82（4）： 1611-1622.

［21］""""" GALVANETTO U， VIOLARIS G. Numerical investigation of a new damage detection method based on proper orthogonal decomposition［J］. Mechanical Systems and Signal Processing， 2007， 21（3）： 1346-1361.

［22］""""" GALVANETTO U， SURACE C， TASSOTTI A. Structural damage detection based on proper orthogonal decomposition： experimental verification［J］. AIAA Journal， 2008， 46（7）： 1624-1630.

［23］""""" WANG D S， XIANG W， ZENG P， et al. Damage identification in shear-type structures using a proper orthogonal decomposition approach［J］. Journal of Sound and Vibration， 2015， 355： 135-149.

［24］""""" AZAM E S， MARIANI S， ATTARI N K A. Online damage detection via a synergy of proper orthogonal decomposition and recursive Bayesian filters［J］. Nonlinear Dynamics， 2017， 89： 1489-1511.

［25］""""" LU K， JIN Y L， CHEN Y S， et al. Review for order reduction based on proper orthogonal decomposition and outlooks of applications in mechanical systems［J］. Mechanical Systems and Signal Processing， 2019， 123： 264-297.

第一作者： 杨少冲（1979―），男，博士，副教授。E-mail：yangshaochong@hbu.edu.cn

通信作者： 方有亮（1967―），男，博士，教授。E-mail：fang_youliang@126.com

基金项目："国家自然科学基金资助项目（12172117）