流形正则化支持高阶张量机及其在行星齿轮箱半监督故障诊断中的应用

摘要： 本文提出了一种基于流形正则化支持高阶张量机（MRSHTM）的行星齿轮箱半监督故障诊断方法。在MRSHTM中引入CP分解挖掘张量数据中的内在结构信息，并定义张量逆多元二次核函数（Tensor‑IMKF）以构建图拉普拉斯算子，从而更好地描述张量数据之间的流形结构。针对多分类问题，将一对多（OVR）策略引入MRSHTM中，提出一对多流形正则化支持高阶张量机（OVR‑MRSHTM）模型。利用层次多尺度排列熵（HMPE）提取多通道振动信号的“通道×层次×尺度”三阶张量故障特征，并输入OVR‑MRSHTM中进行自动识别。实验结果表明，所提算法能够在张量空间中实现稀缺标记样本下的行星齿轮箱智能故障诊断。

关键词： 半监督故障诊断； 行星齿轮箱； 张量学习； 流形正则化

中图分类号： TH165⁺.3； TH132.41""" 文献标志码： A""" 文章编号： 1004-4523（2025）01-0078-10

DOI：10.16385/j.cnki.issn.1004-4523.2025.01.009

Manifold regularized support higher-order tensor machinesfor semi-supervised fault diagnosis of planetary gearboxes

YANG Cheng^1，2， He Qingbo¹， JIA Minping²， LI Zhinong³， PENG Zhike^1，4

（1.State Key Laboratory of Mechanical Systems and Vibration， Shanghai Jiao Tong University， Shanghai 200240， China；2.School of Mechanical Engineering， Southeast University， Nanjing 211189， China；3.Key Laboratory of Nondestructive Testing of Ministry of Education， Nanchang Hangkong University， Nanchang 330063， China；4.School of Mechanical Engineering， Ningxia University， Yinchuan 750021， China）

Abstract： In this study， a novel semi-supervised fault diagnosis of planetary gearboxes based on manifold regularized support higher-order tensor machines （MRSHTM） is proposed. In the MRSHTM， CANDECOMP/PARAFAC （CP） decomposition is introduced to exploit the intrinsic structural information of tensor data， and tensor-based inverse multiquadric kernel function （Tensor-IMKF） is defined to construct a Laplacian operator. The constructed graph matrix can better describe the manifold structure between tensor data. Besides， the one-versus-rest （OVR） strategy is introduced into the MRSHTM model for multi-class fault diagnosis of planetary gearboxes. Hierarchical multiscale permutation entropy （HMPE） is adopted to extract the three-order tensor features “channel×hierarchical layer×scale”， and then the extracted HMPE values are fed into OVR-MRSHTM for automatic fault identification. The results suggest that the proposed method can achieve semi-supervised fault diagnosis of planetary gearboxes in tensor space.

Keywords： semi-supervised fault diagnosis；planetary gearboxes；tensor learning；manifold regularization

行星齿轮箱作为一种重要的传动部件，被广泛应用于工业机器人、风力发电机、直升机、舰船等装备中^［1‑3］。受连续运转、强载荷等非理想工作环境的影响，行星齿轮箱较易发生损坏以致完全失效，从而严重影响装备安全运行。因此，开展行星齿轮箱状态监测与故障诊断的研究，对于确保重大装备安全可靠运行具有重要的意义。

国务院印发的《中国制造2025》国家行动纲领将智能制造作为新一代信息和制造技术融合发展的主攻方向^［4］。作为智能制造的重要一环，基于数据驱动的智能故障诊断能够更有效地处理海量的装备状态数据，已成为大数据下重大装备故障诊断的重要研究方向^［5］。国内外专家学者针对装备中常用传动部件如行星齿轮箱的智能故障诊断展开了深入研究^［6‑10］。胡茑庆等^［6］针对行星齿轮箱振动信号的非平稳性问题，将经验模式分解与深度卷积神经网络相结合，提出了一种行星齿轮箱智能故障诊断方法，可自动识别行星齿轮箱的故障类型。熊鹏等^［7］针对变转速工况环境下行星齿轮箱智能故障诊断问题，提出了动态加权密集连接卷积网络，可自适应地提取不同频带内的故障特征信息，从而自动识别变转速行星齿轮箱故障。王辉等^［8］针对现有行星齿轮箱多工况下故障表征存在的问题，提出了一种基于多尺度注意力深度强化学习网络的行星齿轮箱智能故障诊断算法，提高了诊断精度和工况适应性。然而，以上算法均属于监督学习框架，即需要大量且属于不同类别的典型标记样本来实现有效诊断。在实际工程中，收集大量标记故障样本需要昂贵的代价和人力成本。针对此问题，半监督学习模型被引入行星齿轮箱智能故障诊断中，涌现了很多行之有效的行星齿轮箱半监督故障诊断方法^{［11‑14］}。张鑫等^［11］提出了基于Laplacian特征映射和深度置信网络的半监督故障识别模型，可在较少标记样本下自动识别齿轮裂纹故障；韩特等^［12］提出了一种融合图标签传播和判别特征增强的半监督故障诊断方法，可有效识别工业机器人RV减速器中的齿轮故障。

随着物联网和传感器技术的发展，完备甚至冗余的工业传感器从不同的角度获取了海量蕴含丰富工况信息的多维数据^［15］。在实时测量的多维数据中，蕴含丰富故障信息的张量特征，可尽量保存数据的内在结构信息，以更好地表征设备的运行状态。然而，以上行星齿轮箱智能故障诊断方法仅适用于向量空间，不能直接识别张量特征。若将张量特征融合为“向量特征”，必然会损失张量特征的结构信息；若将张量特征展开为“向量形式”，可能会因此产生高维小样本而导致过拟合问题。近年来，张量学习（tensor learning）^［16］作为传统机器学习模型在张量空间中被推广，因其能够直接处理张量型数据而备受关注。为此，专家学者将张量学习理论引入行星齿轮箱智能故障诊断中，充分利用张量数据的结构信息及其相关性来提升故障识别精度^{［17‑19］}。LI等^［17］提出了辛加权稀疏支持矩阵机，并成功应用于齿轮箱智能故障诊断中。葛江华等^［18］利用支持张量机（support tensor machines，STM）直接识别二阶张量特征，并与集成矩阵距离测度的k近邻分类器融合决策，实现了齿轮箱故障的自动识别。HE等^［19］提出了基于动态惩罚因子的支持高阶张量机模型，并用齿轮箱实例验证了该算法的有效性。

综上所述，传统的行星齿轮箱半监督故障诊断算法仅适用于向量空间；现有的基于张量学习的行星齿轮箱智能故障诊断模型主要是基于标记故障样本充足这一背景下提出的，在少量标记训练样本下难以实现有效地故障诊断。基于此，本文针对张量空间中稀缺标记样本下行星齿轮箱智能故障诊断展开研究具有重要意义。在半监督学习模型中，基于流形正则化（manifold regularization，MR）^［20］的半监督学习是目前主流方法之一，其主要基于流形假设：同一局部领域内的样本数据之间的内在结构关系是紧密相关的，因此它们具有相似的类标签。Laplacian支持向量机^［21］作为一种典型的流形正则化半监督学习算法，充分挖掘样本数据之间的流形结构，并将流形正则化项嵌入SVM模型中的目标函数中，从而提升在稀缺标记样本下的分类能力。支持高阶张量机（support higher‑order tensor machines，SHTM）^［22］能够更好地利用张量特征的内在结构信息，在智能故障诊断中取得了成功应用。

因此，本文将流形正则化引入支持高阶张量机中，提出一种半监督张量学习模型，即流形正则化支持高阶张量机（manifold regularized support higher‑order tensor machines， MRSHTM）。在MRSHTM中，利用图拉普拉斯算子构建流形结构来表征少数标记和大量无标记样本之间的联系。与传统图模型构建不同，本文利用CP分解^［23］提取张量样本中的结构信息，从而进一步描述张量数据中的复杂流形结构。针对多分类问题，本文将一对多（one‑versus‑rest， OVR）^［24］策略引入MRSHTM模型中，提出了一对多流形正则化支持高阶张量机模型（one‑versus‑rest manifold regularized support higher‑order tensor machine， OVR‑MRSHTM）。利用层次多尺度排列熵（hierarchical multi‑scale permutation entropy，HMPE）^［25］提取多通道振动信号的“通道×层次×尺度”三阶张量故障特征，并输入所提的OVR‑MRSHTM模型中进行自动识别，最终给出了一种基于HMPE和OVR‑MRSHTM模型的行星齿轮箱半监督故障诊断方案。试验结果验证了所提算法在稀缺标记样本下行星齿轮箱智能故障诊断的有效性和优越性。

1 层次多尺度排列熵

本文所提的行星齿轮箱半监督故障诊断算法首先引入基于层次多尺度排列熵（HMPE）的特征提取方法，以获取多通道振动数据中蕴含的更详细的故障信息。在HMPE中，引入层次分析将多通道振动数据从高频到低频进行划分，再引入多尺度分析对不同频带的层次子分量进行空间尺度分割，最后引入排列熵评估各子分量的动态复杂性，从而构建“通道×层次×尺度”三阶张量故障特征。

1.1 排列熵

排列熵（permutation entropy，PE）^［26］作为一种量化时间序列复杂性或不确定性的评价指标，能够有效地检测行星齿轮箱系统的动力学特性。PE值的具体计算步骤如下：

（1） 对于给定的时间序列，利用延迟坐标法对其进行相空间重构：

（1）

式中，，"" " 为相空间子分量；为嵌入维数；为延迟时间。

（2） 根据重构的相空间子分量中元素的大小关系，可描述并辨识各子分量中的排列模式。对于嵌入维数，易知嵌入向量最多存在m！种潜在的排列模式。因此，对于每种排列模式，其概率可估计为：

（2）

（3） 根据香农熵（Shannon entropy）的定义，时间序列的排列熵可估计如下：

（3）

进一步，对应的归一化排列熵表示如下：

（4）

式中，。

1.2 HMPE计算流程

对于给定多通道振动数据，其中，，（为通道数）。层次多尺度排列熵的具体计算步骤如下：

（1） 分别定义平均算子和差分算子如下：

（5）

（2） 在平均算子和差分算子的基础上，定义第层矩阵算子如下：

（6）

式中，。

（3） 定义一个维引索向量，第个层次子分量对应唯一引索向量：

（7）

（4） 估计多通道振动数据的各层次分量如下：

（8）

式中，为第个通道振动数据第层的第个节点的层次分量。

（5） 对于每个层次分量，粗粒化的时间序列可通过下式估计得到：

（9）

式中，为尺度因子；t为时间序列。

（6） 通过式（4）计算的PE值，并最终估计多通道振动数据的层次多尺度排列熵：

；

（10）

式中，为通道数；为层次数；为节点数；为最大尺度因子；延迟时间一般设置为1。按照上述步骤对进行处理，可构建得到尺寸为的三阶张量故障特征，通过描述多通道振动数据中不同通道、不同层次以及不同尺度之间的关联，表征更丰富的故障信息。

2 流形正则化支持高阶张量机

在特征提取之后，针对标记故障样本稀缺问题，本文提出一种流形正则化支持高阶张量机（MRSHTM）模型，基于半监督学习中的流形假设，结合少量标记样本和大量无标记样本的张量特征信息，尽可能提高故障诊断效率。

2.1 支持高阶张量机

对于张量样本集的二分类问题，其中，为训练样本数，为张量样本，为样本标签。在支持高阶张量机（support higher‑order tensor machines， SHTM）中，权重向量被超平面权重张量取代。令权重张量（“”为外积运算），利用张量外积和张量的Frobenius范数的定义，可得：

（11）

根据张量‑模乘积和张量内积的定义，可写成如下形式：

（12）

引入松弛变量，利用式（11）和（12），可将原来交替投影算法求解朴素支持张量机模型的个QP问题转化为如下的凸优化问题：

（13）

对于优化问题（13），构造拉格朗日函数，可得：

（14）

式中，和为拉格朗日乘子。进一步，求对、以及的偏导数并置为0，可得：

（15）

（16）

（17）

将式（15）～（17）代入式（14）中，优化问题（13）转化为其对偶问题：

（18）

式中，为和的内积。将张量CP分解嵌入式（18）的内积运算中，以便得到更紧凑且有意义的张量特征表示。根据张量CP分解的定义，和分别可表示为：

（19）

（20）

则和的内积可表示为：

（21）

将式（21）代入式（18），可得：

式（22）为线性SHTM模型。类似于传统支持向量机，模型可由SMO（sequential minimal optimization）算法进行求解。对于测试样本，相应的决策函数可表示为：

（23）

式中，和分别为和的张量CP分解得到载荷矩阵的列向量。

2.2 图拉普拉斯算子

对于张量样本，，…，，构造一个无向加权图，其中，为样本节点，为节点之间的边。对于无向加权图而言，邻接矩阵为图中边的权重。在张量空间中，设中的一个节点为，另一个节点为。利用CP分解对和进行分解，其分解形式分别如式（19）和（20）所示。将逆多元二次核函数扩展到张量空间中，定义张量逆多元二次核函数（Tensor‑IMKF）以衡量不同节点之间的相似性：

（24）

进一步，图拉普拉斯算子定义为：

（25）

式中，为度矩阵，即。

归一化的图拉普拉斯算子可表示为：

（26）

式中，为单位矩阵。由此，构建标记故障样本和无标记故障样本的图拉普拉斯算子，可更好地描述训练样本集的流形结构信息。

2.3 MRSHTM模型

为弥补传统SHTM模型在故障标记样本稀缺情况下分类精度的不足，本文在SHTM模型的基础上加入流形正则项，充分利用少量标记样本和大量无标记样本之间的流形结构信息，建立一种基于流形正则化支持高阶张量机的半监督学习框架。

考虑一个在阶张量空间中的二分类问题（本文中为3），假设有少量标记张量样本集和大量无标记张量样本集，其中为样本标签。对于MRSHTM模型，半监督流形正则化框架可定义为：

（27）

式中，为标记样本的损失函数；为正则项；为流形正则项，用于控制决策函数在概率分布的内在几何结构上的复杂度；和为正则项权重。

在流形正则化支持高阶张量机模型中，设定损失函数为hinge损失函数：

（28）

根据决策函数，MRSHTM模型的正则项为，其中：

（29）

式中，；为核函数。

引入图拉普拉斯算子，得到MRSHTM模型的流形正则项为：

（30）

式中， 。

通过最小化式（30），确保流形距离相近的样本具有相似的标签。基于流形假设，利用少量标记张量样本和大量无标记张量样本之间的流形结构赋予大量无标记张量样本“标签信息”，使之在张量分类器优化求解中起到“监督”作用，从而有效提高分类性能。将式（28）和（30）代入式（27）中，则MRSHTM模型的优化问题为：

（31）

式中，，。

为了求解式（31），通过引入拉格朗日乘子和，得到拉格朗日函数：

（32）

式中，为松弛变量。

对于和的偏导，分别表示为：

（33）

（34）

将式（33）和（34）代入式（32）中，可得：

式中，；为单位矩阵；。

得到关于的偏导数并置为0，可得：

（36）

式中，为的最优解。

因此，式（31）的对偶问题可写成：

（37）

其中：

（38）

最后，MRSHTM模型的决策函数表示为：

（39）

式中，为训练样本数；为CP分解模型因子；为拉格朗日乘子；和分别为训练张量样本集和测试张量样本集的张量CP分解得到载荷矩阵的列向量；为偏置项，可表示为：

（40）

2.4 多分类流形正则化支持高阶张量机

本文将上述模型从二分类问题推广到多分类问题中，引入一对多（one‑versus‑rest， OVR）策略到MRSHTM模型中，提出了一对多流形正则化支持高阶张量机（one‑versus‑rest manifold regularized support higher‑order tensor machine， OVR‑MRSHTM）模型。其主要思路是将一个类分类问题转化为个二分类问题，通过构造出个最优化问题，求解得到个张量决策超平面。在构造第个最优化问题时，把训练集中个样本分为两部分，其中原本属于第类的样本归为“+1”类，将剩余类样本归为“-1”类，形成一个二分类问题。OVR‑MRSHTM模型的决策函数为：

（41）

式中，上标（h）表示类别。

3 实例验证与分析

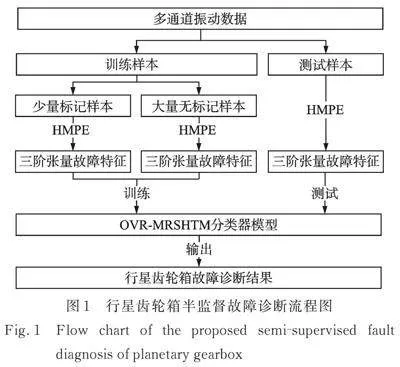
本文将层次多尺排列熵（HMPE）和流形正则化支持高阶张量机（MRSHTM）相结合，提出一种行星齿轮箱半监督故障诊断方法，如图1所示。给出具体步骤如下：

（1） 从安装在行星齿轮箱上的传感器中同步采集不同故障状态下的多通道振动数据。

（2） 在HMPE算法中分别设置层次数、尺度因子、嵌入维数等，利用HMPE算法从各通道振动信号中提取二阶张量特征。

（3） 对于每个样本，将各通道的二阶张量特征进行堆叠，从而构建“通道×层次×尺度”的三阶张量故障特征。

（4） 从总样本中随机选出少量标记样本和大量无标签样本作为训练样本，其余样本则为测试集。

（5） 设置MRSHTM模型中的参数，利用训练样本集的三阶张量故障特征对OVR‑MRSHTM模型进行训练，得到决策函数。

（6） 利用决策函数对测试样本集的三阶张量故障特征进行自动识别，最终得到行星齿轮箱故障诊断结果。

为了验证所提流形正则化支持高阶张量机在行星齿轮箱半监督故障诊断中的有效性，本文选用无锡厚德自动化仪表公司提供的型号为HD‑CL‑012X的行星齿轮箱综合故障模拟实验台。该实验台主要由3 kW三相感应电机、电机变频器、联轴器、行星故障模拟齿轮箱、磁粉制动器、加载控制器、数据采集系统等部分组成，其实景图如图2所示。实验中，将型号为PCB356B21的三轴加速度传感器布置在行星齿轮箱正上方位置（如图3所示），采样频率设置为12000 Hz。利用电火花技术分别在太阳轮齿轮、行星轮齿轮以及齿轮外圈上模拟了齿根裂纹故障，故障齿轮如图4所示。在此设置工况环境：负载为0，转速为1200 r/min。对于每类故障齿轮，将采集的振动数据不重叠划分为100个样本，每个样本尺寸为3×2048，其他样本信息如表1所示。

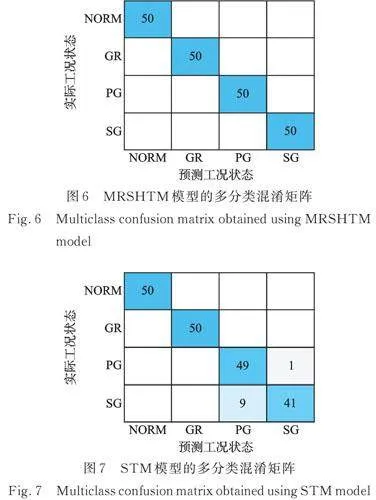
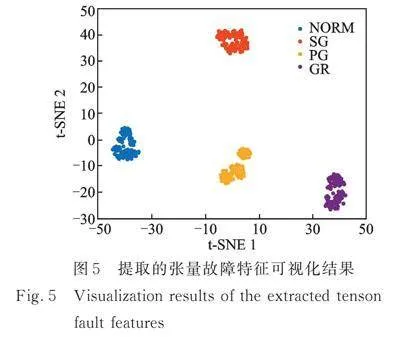
根据第3节所述的智能故障诊断流程，首先利用层次多尺度排列熵（HMPE）对三轴加速度传感器采集的多通道振动信号进行特征提取，从而构造得到“层次×尺度×通道”形式的三阶张量故障特征。在HMPE中，具体参数设置如下：层次数为4，尺度因子为16，嵌入维数为4。利用T分布随机近邻嵌入（T‑distribution stochastic embedding，T‑SNE）将所提取的张量故障特征可视化到二维平面中，如图5所示。由图5可知，所提三阶张量故障特征具有良好的同类聚集性和异类可分性。然后，从每个齿轮箱故障类型100个样本中随机选择5个样本作为有标签训练样本，再选择45个样本作为无标签样本，剩余的50个样本作为测试样本。设置半监督学习模型MRSHTM的具体参数如下：CP模型分解因子为2，正则项权重为1，为10³，为1。接着，利用20个有标签样本和180个无标签样本对所提OVR‑MRSHTM半监督分类模型进行训练，并利用其余的200个样本对训练好的OVR‑MRSHTM分类模型进行测试。同时，将一对多分类策略引入原始的支持张量机（support tensor machines，STM）中进行对比分析。图6和7分别给出了MRSHTM半监督模型和STM模型的多分类混淆矩阵。从图6和7中可以看出，所提MRSHTM模型能够在少数标签样本情况下完全识别测试样本的故障状态，而未加入流形正则化的STM模型有1个PG类样本被错分为SG类且有9个SG类样本被错分为PG类，其故障识别率为95%。为了定量对比所提MRSHTM模型与传统STM模型，选取三种常见的评价指标，即精确率P_r、召回率R_c以及F1分数F₁，其具体计算公式如下：

（42）

（43）

（44）

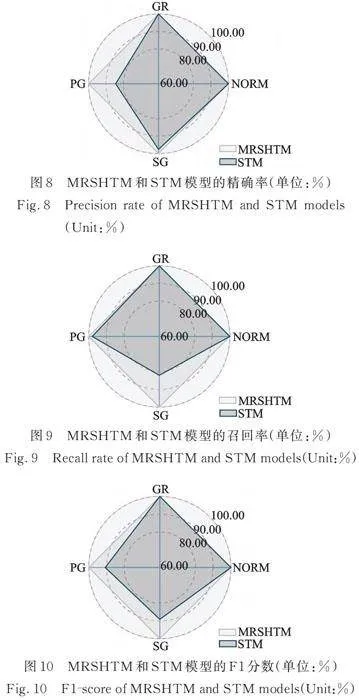
式中，为真正例，为假反例，为假正例。于是，上述混淆矩阵对应的各类故障状态评价指标如图8～10所示。从评价指标来看，所提MRSHTM模型能够很好地识别齿轮箱各故障状态，而传统STM模型对于标签为NORM类和GR类的故障识别效果明显差于MRSHTM模型。

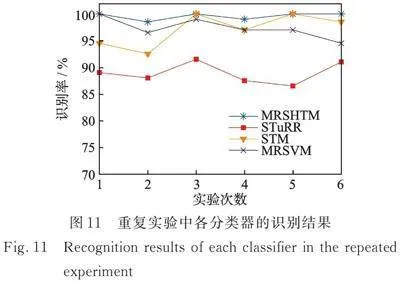
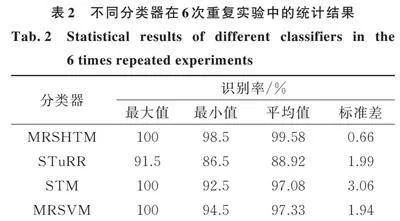
为了验证所提算法的优越性，引入其他几种相关的半监督分类模型，如半监督Tucker岭回归（semi‑supervised tucker ridge regression， STuRR）、流形正则化支持向量机（manifold regularized support vector machines，MRSVM）进行比较分析。同样，从每个齿轮箱故障类型样本中随机选择5个样本作为有标签训练样本，再选择45个样本作为无标签样本，剩余的50个样本作为测试样本。为了避免随机选择偶然性的影响，MRSHTM、STuRR、STM和MRSVM这四种分类模型均进行6次重复实验，故障识别结果如图11所示。从多次重复实验结果来看，所提MRSHTM模型均具有最高的故障识别率。为了进一步量化各比较算法的识别性能，给出上述重复试验识别结果的相关统计指标（最大值、最小值、平均值以及标准差）如表2所示。从表2中可以看出，所提的MRSHTM模型具有最高的平均识别率，且标准差最低。这表明所提算法在齿轮箱半监督故障诊断中不仅识别效果最好，且在稳定性方面也强于其他比较算法。STM模型的识别效果差于所提算法，且稳定性最差，主要原因在于STM模型仅利用少数标签样本而无法利用大量无标签训练样本确定决策边界。相比MRSVM模型，MRSHTM模型能够充分利用张量特征的内在结果信息，更好地描述张量数据中的复杂流形结构。

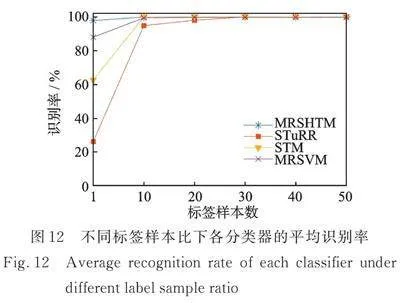
为了评估不同标签样本比对所提算法的影响，将标签样本比（标签样本数/总训练样本数）分别设置为1/50、10/50、20/50、30/50、40/50和50/50。即从每个齿轮箱故障类型样本中随机选择50个样本作为训练样本，其余的50个样本作为测试样本。其中，根据不同的标签样本比，将训练样本集划分为有标签训练样本集和无标签训练样本集。为了避免随机选择偶然性的影响，各比较算法在不同的标签样本比下均重复10次实验。图12给出了不同标签样本比下各分类器的平均识别率。从图12中可以看出，在标签样本比极低（2%）的情况下，所提MRSHTM模型的平均故障识别率接近98%，其识别效果明显好于其他比较算法。随着标签样本比的增长，各比较算法的故障识别效果也随之增长。具体地，在标签样本比超过40%时，各比较算法的故障识别率均接近100%。

4 结" 论

针对张量空间中少标签样本下行星齿轮箱智能故障诊断问题，提出了一种半监督张量学习模型，即流形正则化支持高阶张量机（MRSHTM）。给出主要结论如下：

（1） 在所提的MRSHTM模型中，引入了CP分解挖掘张量数据中的内在结构信息，并定义了张量逆多元二次核函数（Tensor‑IMKF），从而构建得到图拉普拉斯算子，可更好地描述张量数据之间的流形结构。

（2） 所提的MRSHTM模型基于流形假设，利用图拉普拉斯算子建立少数标签样本和大量无标签样本之间的联系以实现标签信息传递，从而充分利用大量无标签样本辅助模型训练，有效提升了少标签样本下的故障识别率。

（3） 利用实验室行星齿轮箱故障数据对所提算法进行了验证，结果表明所提算法在少标签样本下仍能实现对行星齿轮箱故障的有效诊断。

参考文献：

［1］""""""" WEI S， WANG D， PENG Z K， et al. Variational nonlinear component decomposition for fault diagnosis of planetary gearboxes under variable speed conditions［J］. Mechanical Systems and Signal Processing， 2022， 162： 108016.

［2］""""""" HILBERT M， SMITH W A， RANDALL R B. The effect of signal propagation delay on the measured vibration in planetary gearboxes［J］. Journal of Dynamics， Monitoring and Diagnostics， 2022， 1（1）： 9-18.

［3］""""""" 雷亚国， 汤伟， 孔德同， 等. 基于传动机理分析的行星齿轮箱振动信号仿真及其故障诊断［J］. 机械工程学报， 2014， 50（17）： 61-68.

LEI Y G， TANG W， KONG D T，et al. Vibration signal simulation and fault diagnosis of planetary gearboxes based on transmission mechanism analysis［J］. Journal of Mechanical Engineering， 2014， 50（17）： 61-68.

［4］""""""" 周济. 智能制造——“中国制造2025”的主攻方向［J］. 中国机械工程， 2015， 26（17）： 2273-2284.

ZHOU J. Intelligent manufacturing——main direction of “made in China 2025”［J］. China Mechanical Engineering， 2015， 26（17）： 2273-2284.

［5］""""""" 雷亚国， 贾峰， 孔德同， 等. 大数据下机械智能故障诊断的机遇与挑战［J］. 机械工程学报， 2018， 54（5）：94-104.

LEI Y G， JIA F， KONG D T， et al. Opportunities and challenges of machinery intelligent fault diagnosis in big data era［J］. Journal of Mechanical Engineering， 2018， 54（5）： 94-104.

［6］""""""" 胡茑庆， 陈徽鹏， 程哲， 等. 基于经验模态分解和深度卷积神经网络的行星齿轮箱故障诊断方法［J］. 机械工程学报， 2019， 55（7）： 9-18.

HU N Q， CHEN H P， CHENG Z， et al. Fault diagnosis for planetary gearbox based on EMD and deep convolutional neural networks［J］. Journal of Mechanical Engineering， 2019， 55（7）： 9-18.

［7］""""""" 熊鹏， 汤宝平， 邓蕾， 等. 基于动态加权密集连接卷积网络的变转速行星齿轮箱故障诊断［J］. 机械工程学报， 2019， 55（7）： 52-57.

XIONG P， TANG B P， DENG L， et al. Fault diagnosis for planetary gearbox by dynamically weighted densely connected convolutional networks［J］. Journal of Mechanical Engineering， 2019， 55（7）： 52-57.

［8］""""""" 王辉， 徐佳文， 严如强. 基于多尺度注意力深度强化学习网络的行星齿轮箱智能诊断方法［J］. 机械工程学报， 2022， 58（11）： 133-142.

WANG H， XU J W， YAN R Q. Multi-scale attention based deep reinforcement learning for intelligent fault diagnosis of planetary gearbox［J］. Journal of Mechanical Engineering， 2022， 58（11）： 133-142.

［9］""""""" SHI J C， PENG D K， PENG Z X， et al. Planetary gearbox fault diagnosis using bidirectional-convolutional LSTM networks［J］. Mechanical Systems and Signal Processing， 2022， 162： 107996.

［10］""""" ZHAO D Z， CUI L L， CHU F L. Synchro-reassigning scaling Chirplet transform for planetary gearbox fault diagnosis［J］. IEEE Sensors Journal， 2022， 22（15）： 15248-15257.

［11］""""" 张鑫， 郭顺生， 李益兵， 等. 基于拉普拉斯特征映射和深度置信网络的半监督故障识别［J］. 机械工程学报， 2020， 56（1）： 69-81.

ZHANG X， GUO S S， LI Y B， et al. Semi-supervised fault identification based on Laplacian eigenmap and deep belief networks［J］. Journal of Mechanical Engineering， 2020， 56（1）： 69-81.

［12］""""" 韩特， 李彦夫， 雷亚国， 等. 融合图标签传播和判别特征增强的工业机器人关键部件半监督故障诊断方法［J］. 机械工程学报，2022，58（17）： 116-124.

HAN T， LI Y F， LEI Y G， et al， Semi-supervised fault diagnosis method via graph label propagation and discriminative feature enhancement for critical components of industrial robot［J］. Journal of Mechanical Engineering，2022，58（17）： 116-124.

［13］""""" ZHOU K， DIEHL E， TANG J. Deep convolutional generative adversarial network with semi-supervised learning enabled physics elucidation for extended gear fault diagnosis under data limitations［J］. Mechanical Systems and Signal Processing， 2023， 185： 109772.

［14］""""" ZHANG X L， SU Z Q， HU X L， et al. Semisupervised momentum prototype network for gearbox fault diagnosis under limited labeled samples［J］. IEEE Transactions on Industrial Informatics， 2022，18（9）： 6203-6213.

［15］""""" 赵春晖， 余万科， 高福荣. 非平稳间歇过程数据解析与状态监控——回顾与展望［J］. 自动化学报， 2020， 46（10）： 2072-2091.

ZHAO C H， YU W K， GAO F R. Data analytics and condition monitoring methods for nonstationary batch processes — current status and future［J］. Acta Automatica Sinica， 2020， 46（10）： 2072-2091.

［16］""""" SIDIROPOULOS N D， DE LATHAUWER L， FU X， et al. Tensor decomposition for signal processing and machine learning［J］. IEEE Transactions on Signal Processing， 2017， 65（13）： 3551-3582.

［17］""""" LI X， YANG Y， SHAO H D， et al. Symplectic weighted sparse support matrix machine for gear fault diagnosis［J］. Measurement， 2021， 168： 108392.

［18］""""" 葛江华， 刘奇， 王亚萍， 等. 支持张量机与KNN-AMDM决策融合的齿轮箱故障诊断方法［J］. 振动工程学报， 2018， 31（6）： 1093-1101.

GE J H， LIU Q， WANG Y P， et al. Fault diagnosis method of gearbox supporting tension machine and KNN-AMDM decision fusion［J］. Journal of Vibration Engineering， 2018， 31（6）： 1093-1101.

［19］""""" HE Z Y， SHAO H D， CHENG J S， et al. Support tensor machine with dynamic penalty factors and its application to the fault diagnosis of rotating machinery with unbalanced data［J］. Mechanical Systems and Signal Processing， 2020， 141： 106441.

［20］""""" BELKIN M， NIYOGI P， SINDHWANI V. Manifold regularization： a geometric framework for learning from labeled and unlabeled examples［J］. Journal of Machine Learning Research， 2006， 7（1）： 2399-2434.

［21］""""" LI Z R， KANG Y， FENG D Y， et al. Semi-supervised learning for lithology identification using Laplacian support vector machine［J］. Journal of Petroleum Science and Engineering， 2020， 195： 107510.

［22］""""" HAO Z F， HE L F， CHEN B Q， et al. A linear support higher-order tensor machine for classification［J］. IEEE Transactions on Image Processing， 2013， 22（7）： 2911-2920.

［23］""""" GOULART J H M， BOIZARD M， BOYER R， et al. Tensor CP decomposition with structured factor matrices： Algorithms and performance［J］. IEEE Journal of Selected Topics in Signal Processing， 2016， 10（4）： 757-769.

［24］""""" DING S F， ZHAO X Y， ZHANG J， et al. A review on multi-class TWSVM［J］. Artificial Intelligence Review， 2019， 52（2）： 775-801.

［25］""""" YANG C， JIA M P. Hierarchical multiscale permutation entropy-based feature extraction and fuzzy support tensor machine with pinball loss for bearing fault identification［J］. Mechanical Systems and Signal Processing， 2021， 149： 107182.

［26］""""" BANDT C， POMPE B. Permutation entropy： a natural complexity measure for time series［J］. Physical Review Letters， 2002， 88（17）： 174102.

第一作者："杨" 诚（1993―），男，博士后。E-mail：yangcheng23@sjtu.edu.cn

通信作者："彭志科（1974―），男，博士，教授。E-mail：z.peng@sjtu.edu.cn

基金项目："国家自然科学基金创新研究群体项目（12121002）；国家自然科学基金资助项目（52075095）；“两机”重大专项基础研究项目（J2019-IV-0018-0086）；中国博士后面上基金资助项目（2023M742254）