仿生肢状准零刚度隔振系统的振动特性研究

摘要： 在低频隔振领域，针对线性系统存在承载能力不足及传统准零刚度隔振系统存在刚度硬化，非线性跳跃导致系统失稳的问题，以仿生肢状结构作为负刚度元件与正刚度弹簧并联建立了仿生肢状准零刚度隔振系统的力学模型，分析了系统的静力学特性；基于拉格朗日方程建立动力学模型，采用谐波平衡法进行解析求解；通过理论分析和试验研究对比分析了线性、传统准零刚度隔振系统和仿生肢状准零刚度隔振系统隔振特性，以及激励幅值对系统隔振性能和稳定特性的影响规律。结果表明：相比线性系统和传统准零刚度隔振系统，仿生肢状准零刚度隔振系统不仅保证了系统具有较高的承载能力，而且通过结构参数设计有效降低了位移传递率，拓展了隔振频宽，提高了系统在复杂激励环境中的稳定性和隔振性能。

关键词： 低频隔振； 仿生肢状结构； 准零刚度； 位移传递率； 被动隔振

中图分类号： O328； R318.17""" 文献标志码： A""" 文章编号： 1004-4523（2025）01-0029-10

DOI：10.16385/j.cnki.issn.1004-4523.2025.01.004

Research on vibration characteristics of bionic limb-like quasi-zero stiffness isolation system

LIU Haichao， YAN Ming， JIN Yingli， Sun Ziqiang， WANG Kaiping， YANG Ning

（Engineering Research Center of Impact Protection and Damage Assessment Technology in Liaoning Province，Shenyang University of Technology， Shenyang 110870， China）

Abstract： In the field of low-frequency vibration isolation， aiming at the issues of insufficient bearing capacity of linear system and stiffness hardening and instability caused by nonlinear jump of traditional quasi-zero stiffness vibration isolation system， a mechanical model of the bionic limb-like quasi-zero stiffness isolation system was established by using the bionic limb-like structure as the negative stiffness element and the positive stiffness spring in parallel. The static characteristics of the system were analyzed； A dynamic model was established based on the Lagrangian equations， and the harmonic balance method was used to analyze the dynamics equations of the system analytically； Through theoretical analysis and experimental research， the isolation characteristics of linear and traditional quasi-zero stiffness isolation system and bionic limb quasi-zero stiffness isolation system were compared and analyzed， as well as the influence of excitation amplitude on the isolation performance and stability characteristics of the system. The results show that compared with the linear system and the traditional quasi-zero stiffness isolation system， the bionic limb-like quasi-zero stiffness isolation system not only ensures the system has a higher bearing capacity， but also effectively reduces the displacement transmissibility and expands the vibration isolation through the design of structural parameters. The frequency bandwidth improves the stability and vibration isolation performance of the system in complex excitation environments.

Keywords： low frequency vibration isolation； bionic limb structure；quasi-zero stiffness； displacement transmissibility rate； passive vibration isolation

随着中国舰船制造技术的快速发展，舰船设备日益精密化与智能化，但其所处的工作环境更为复杂多变，这对舰船设备隔振装置提出了更高的设计要求，即不仅需要更高的承载能力，而且需要更优的隔振特性^［1⁃2］。已知当激励频率高于固有频率倍时，线性隔振器开始起到隔振作用，只有降低固有频率，即线性弹簧刚度，才能实现更低频率的振动隔离，但此时系统承载能力较低，易导致侧向失稳等问题。显然线性隔振器已经不能满足工程实际需求，而准零刚度隔振器是将负刚度元件引入正刚度系统中，使其在平衡位置附近的工作区间内具有较高的静承载能力和较低的动态刚度，即高静低动特性，因此近年来得到了国内外学者广泛而深入的研究^［3⁃4］。

CARRELLA等^［5⁃7］提出了一种由对称斜弹簧与竖直弹簧并联组成的三弹簧准零刚度隔振器，研究了结构参数对系统静力学性能、力传递率和位移传递率的影响规律，结果表明，相比线性系统，在合理参数条件下，三弹簧准零刚度隔振系统具有更优的隔振性能。赵权等^［8］进一步对三弹簧结构进行了优化，设计了一种占比空间小、便于安装的车载准零刚度隔振器，在考虑加工误差的前提下，通过理论、仿真和振动试验的方法分析了系统参数和激励幅值对位移传递率的影响。结果表明，该结构有效提高了系统振动性能，但随激励幅值增加，系统位移传递率幅值大幅提高，稳定性大幅降低。LIU等^［9］采用欧拉屈曲梁作为负刚度元件构建准零刚度隔振器，利用谐波平衡法对系统动力学方程进行求解，分析了系统参数对隔振性能的影响。结果表明，在一定频率范围内该隔振系统有效降低了系统传递率幅值，提高了系统的振动隔离效果。HUANG等^{［10⁃12］}进一步研究了载荷的扰动、系统的缺陷、激励幅值的变化及冲击载荷的作用等工况下准零刚度隔振系统的振动特性。结果表明，相比线性隔振系统，在低幅振动的条件下，系统具有更为优越的隔振性能，但随着激励幅值的变化，系统会表现出软化、硬化和软化⁃硬化等复杂的非线性动力学特性。利云云等^［13］将欧拉屈曲梁引入双层隔振系统中，建立了双层准零刚度隔振系统动力学模型，根据上下两层的刚度约束关系和限制条件给出了刚度有效取值范围，并对系统隔振性能进行了研究。结果表明，采用上层线性、下层准零刚度时系统具有最好的隔振性能。ZHOU等^［14］、WANG等^［15］以圆凸轮⁃滚子⁃弹簧为负刚度元件，建立了考虑凸轮与滚子可能脱离的分段非线性动力学模型，采用平均法进行解析求解，研究了系统的静力学和动力学特性。结果表明，在准零刚度区间内该系统的力传递率峰值和起始隔振频率均优于线性隔振系统，但由于强非线性，系统依然存在明显的跳频现象。AHN等^［16］从理论设计出发，提出了非圆凸轮型线的设计方法。YAO等^［17］根据实际工作条件设计了一种力⁃位移关系呈分段线性函数变化的非圆凸轮型线，构建准零刚度隔振系统，采用平均法得到了基础激励下系统的动态响应，研究了系统的稳定性和参数影响规律。结果表明，该系统具有更宽的隔振频率范围和更小的响应幅值，但随着激励幅值增加，系统位移传递率增加，隔振性能下降。因此，相对线性隔振系统，上述准零刚度隔振系统在理想条件下均能有效降低系统位移传递率，实现低频隔振，但其隔振性能对激励幅值变化较为敏感，因此更适用于激励载荷恒定的工作环境中。

近年，随着仿生学的快速发展，SUN等^［18］、DAI等^［19］、JIANG等^［20］受动物腿部结构的启发提出了一种仿生肢状结构，并对其力学特性进行了深入研究，结果表明，仿生肢状结构不仅结构简单，便于调节，具有良好的承载能力和低频隔振性能，而且仿生肢状结构在压缩过程中的力⁃位移曲线呈现先增加后减小到零的变化规律，即整个变形区间由正刚度区间和负刚度区间两部分组成。但为了保证仿生肢状结构运动过程中的稳定性，上述文献研究中均将正刚度区间作为有效工作区间，研究了仿生肢状结构在该区间内的力学性能和振动特性，而负刚度区间作为无效区间，其特殊的力学性能并未得到充分的研究与利用。

1 模型构建及静力学特性分析

1.1 力学模型

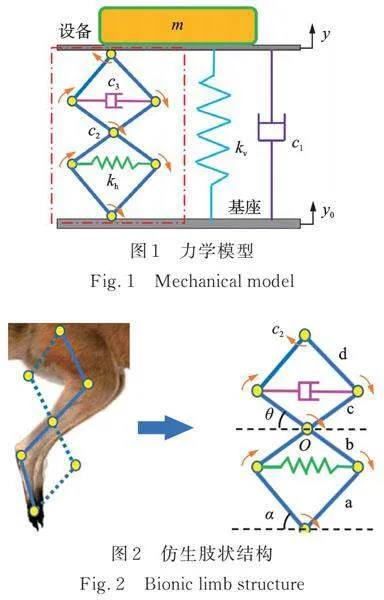
仿生肢状准零刚度隔振系统的力学模型如图1所示，由仿生负刚度结构（图中矩形点划线圈出部分）与垂向正刚度弹簧并联后，一端与质量为m的设备连接，另一端与基座连接。图中，k_v和c₁分别为垂向正刚度弹簧的刚度和阻尼；仿生负刚度结构为受动物在跳跃着陆时利用下肢弯曲、肌肉变形来有效吸收地面的振动与冲击的启发，提出的一种采用连杆a，b，c，d模拟骨骼，7个旋转铰链模拟关节，水平刚度k_h和水平阻尼c₃模拟肌肉变形过程中的刚度与阻尼系数，阻尼c₂模拟关节转动过程中总的旋转阻尼系数的仿生肢状结构，具体结构及参数如图2所示。同时为了便于结构参数的设计与调整，本文研究的仿生肢状结构是关于图2中O点的中心对称结构，杆长关系可以表示为L_a=L_d=L₁，L_b=L_c=L₂，α和θ分别为连杆a和c与水平方向的夹角。

1.2 静力学分析

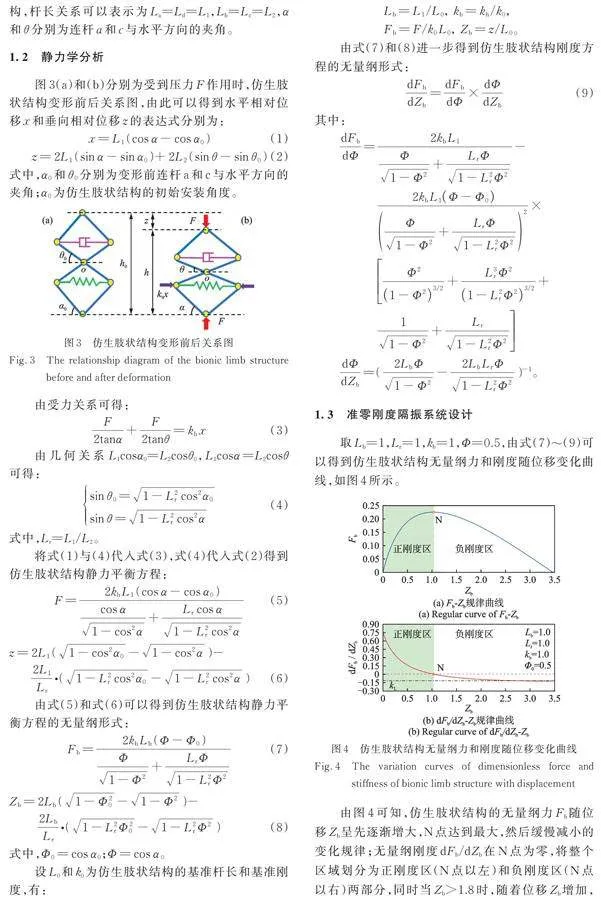
图3（a）和（b）分别为受到压力F作用时，仿生肢状结构变形前后关系图，由此可以得到水平相对位移x和垂向相对位移z的表达式分别为：

（1）

（2）

式中，和分别为变形前连杆a和c与水平方向的夹角；为仿生肢状结构的初始安装角度。

由受力关系可得：

（3）

由几何关系L₁cosα₀=L₂cosθ₀，L₁cosα=L₂cosθ可得：

（4）

式中，L_r=L₁/L₂。

将式（1）与（4）代入式（3），式（4）代入式（2）得到仿生肢状结构静力平衡方程：

（5）

（6）

由式（5）和式（6）可以得到仿生肢状结构静力平衡方程的无量纲形式：

（7）

（8）

式中，；。

设L₀和k₀为仿生肢状结构的基准杆长和基准刚度，有：

由式（7）和（8）进一步得到仿生肢状结构刚度方程的无量纲形式：

（9）

其中：

。

1.3 准零刚度隔振系统设计

取L_b=1，L_r=1，k_b=1，Φ=0.5，由式（7）～（9）可以得到仿生肢状结构无量纲力和刚度随位移变化曲线，如图4所示。

由图4可知，仿生肢状结构的无量纲力F_b随位移Z_b呈先逐渐增大，N点达到最大，然后缓慢减小的变化规律；无量纲刚度dF_b/dZ_b在N点为零，将整个区域划分为正刚度区（N点以左）和负刚度区（N点以右）两部分，同时当Z_bgt;1.8时，随着位移Z_b增加，dF_b/dZ_b的值逐渐趋近常数（用k_L表示），即呈现线性负刚度特性。

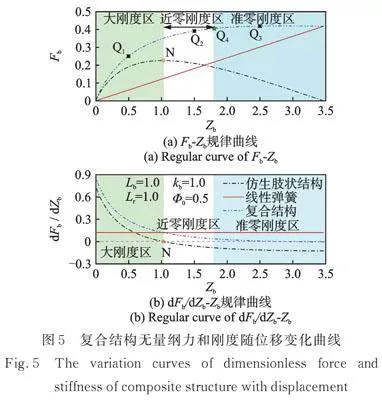
因此，可以选用刚度k_v=|k_L|的正刚度线性弹簧与仿生肢状结构并联，使得复合结构在Z_bgt;1.8时复合刚度近似为零，系统具有准零刚度特性。图5为复合结构的无量纲力和无量纲刚度随位移变化曲线。

由图5可知，复合结构的无量纲力F_b与位移Z_b呈正相关，且当Z_bgt;1.8时，F_b趋于定值，同时系统的承载能力大幅提高；无量纲刚度dF_b/dZ_b与位移Z_b呈负相关，且当Z_bgt;1.8时，dF_b/dZ_b趋近于零，此时系统具有准零刚度特性。因此可以根据刚度特性划分区域，即当0≤Z_blt;1.1时为大刚度区，系统具有较强的非线性刚度，承载能力较低；当1.1≤Z_b＜1.8时为近零刚度区域，系统具有较弱的非线性刚度，承载能力得到大幅提高；当Z_b≥1.8时为准零刚度区，系统具有较高的承载能力以及较低的动态刚度。

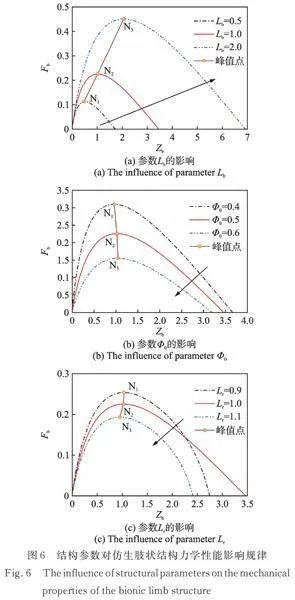
由图6（a）可知，随着参数L_b的增大，无量纲力F_b峰值点N₁～N₃的连线随Z_b增加呈线性增加的趋势，因此，增加参数L_b不仅提高了系统的承载能力，而且扩大了负刚度区域，但负刚度区的线性负刚度k_L不随L_b的增加而发生变化；由图6（b）可知，随着参数的增加，不仅系统的承载能力大幅下降，负刚度区域随之减少，而且负刚度区的线性负刚度k_L值也随之减小；由图6（c）可知，随着参数L_r的增加，系统的承载能力大幅降低，而且以L_r=1为界，参数L_r向两侧变化均导致负刚度区域的减小和线性负刚度k_L值的增大。

综上，增加杆长L_b、增大初始安装角度α₀和适当减小杆长比L_r有利于提高系统的静力学性能。

2 动力学方程的建立与求解

在动力学分析中，考虑了仿生肢状准零隔振系统的垂向线性阻尼c₁、旋转阻尼c₂以及水平阻尼c₃的作用，忽略连杆质量影响，利用拉格朗日原理建立系统动力学方程，并采用谐波平衡法进行求解。其中y₀为作用在基座上的谐波激励，y为设备绝对位移响应，z为设备相对位移响应，即z=y-y₀。

系统动能可以表示为：

（10）

势能为：

（11）

根据拉格朗日原理有：

（12）

式中，L=T-V为朗格朗日函数；D₁，D₂和D₃分别为运动过程中垂向线性阻尼、旋转摩擦阻尼和水平线性阻尼的耗散能，由此可得：

（13）

（14）

将式（13），（14）代入式（12）可得：

（15）

其中：

（16）

采用泰勒级数将式（16）中的f₁（z），f₂（z）和f₃（z）展开得到其近似解公式分别为：

（17）

式中，～为展开式的各级系数；～为展开式的各级系数；～为展开式的各级系数；

将式（17）代入式（15）可得：

（18）

将式（18）无量纲化可以得到：

（19）

其中：

由于系统在零平衡位置具有非对称刚度和阻尼，因此将激励方程和响应方程设为：

（20）

式中，τ=ω₁t；Ω=ω/ω₁；A为基础激励幅值；B₀为位移偏置；B和φ分别为谐波响应幅值和相位角。

将式（20）代入式（19），通过谐波平衡法求得：

（21）

（22）

（23）

联立式（21）～（23）可以求出任意Ω下的响应幅值B和位移偏置B₀。

位移传递率作为评价隔振系统隔振性能的重要指标，定义为设备的位移幅值与激励幅值的比值，即：

（24）

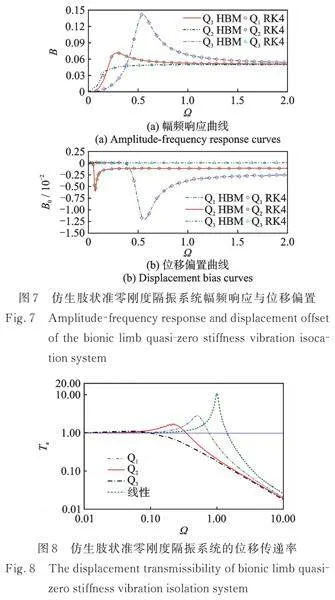
同样选取L_b=1， L_r=1， k_b=1，Φ=0.5，同时在图5中复合结构F_b⁃Z_b特性曲线的不同区域分别选择一个振动平衡点（大刚度区为Z_b=0.5的Q₁点，近零刚度区为Z_b=1.5的Q₂点，准零刚度区为Z_b=2.5的Q₃点）对其幅频响应和位移传递率特性进行了研究，如图7，8所示。

由图7可知，仿生肢状隔振系统在全区域均具有较弱的非线性刚度，因此避免了传统准零刚度隔振器非线性跳跃等不稳定现象。对于大刚度区的振动平衡点Q₁，幅频响应峰值较大，位移偏置现象明显；随着平衡点向右移动到近零刚度区的Q₂点，幅频响应峰值和位移偏置大幅降低；当振动平衡点为准零刚度区Q₃点时，幅频响应峰值达到最小，位移偏置接近为零，说明准零刚度区的仿生肢状隔振系统近似线性系统。同时，由于四阶龙格⁃库塔法得到的仿真曲线与由谐波平衡法得到的解析曲线具有较好的一致性，从而有效验证了理论计算模型的准确性。

由图8可知，相对于线性隔振系统，仿生肢状准零刚度隔振系统绝对位移传递率共振峰值至少降低了74%（具体数据如表1所示），并且随着振动平衡点由Q₁移动到Q₃，主共振频率向左移动，主共振峰值进一步减小，隔振起始频率进一步降低，Q₃点传递率共振峰值仅为1.11，隔振起始频率仅为0.085，同时具有良好的高频隔振性能。因此，仿生肢状准零刚度隔振系统在整个运动行程内的隔振性能均优于线性隔振系统，而且在准零刚度区域内，不仅实现低频超低频隔振，保证了良好的高频隔振性能。

3 隔振特性的分析与讨论

3.1 结构参数对振动性能影响

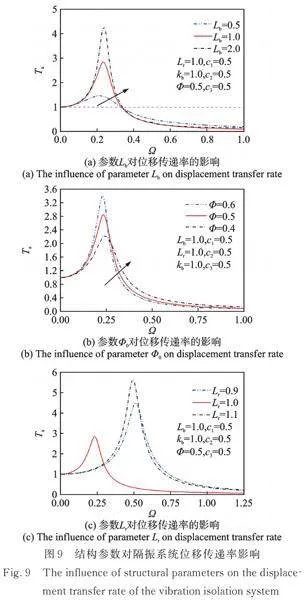
为了更好地研究仿生肢状准零刚度隔振系统的振动特性，首先在图5中复合结构F_b⁃Z_b特性曲线上选定Z_b=1.8对应的Q₄点作为隔振系统振动平衡点，垂向线性阻尼c₁=0.5、旋转阻尼c₂=0.5以及水平阻尼c₃=5.0，激励幅值A=0.10，分析了无量纲参数L_b、Φ₀（Φ₀=cosα₀）和L_r对隔振系统绝对位移传递率特性的影响规律，如图9所示。其中，箭头标注方向为参数增大的方向。

由图9（a）可知，随着参数L_b的减小，隔振系统的共振峰值大幅降低，隔振性能得到提高；由图9（b）可知，随着参数Φ₀的减小（即初始安装角α₀的增大），不仅能够使隔振系统的共振峰值迅速减小，而且能够保证高频区具有良好的隔振性能；由图9（c）可知，无论增大还是减小杆长比L_r，均会导致隔振系统的主共振峰值的大幅增加，起始隔振频率右移，隔振频带变窄，因此在设计仿生肢状准零刚度隔振系统时优先选择参数L_r=1进行结构设计。

综上所述，在设计仿生肢状准零刚度隔振系统时，首先优先选择杆长比L_r=1的参数进行结构设计，然后通过减小杆长L_b，增大初始安装角α₀来进一步提高隔振系统的隔振性能。

3.2 与线性、传统准零刚度隔振系统的对比分析

为了进一步说明仿生肢状准零刚度隔振系统具有的优良隔振性能，本文选择经典三弹簧模型构建传统准零刚度隔振系统进行对比分析，具体计算参数如表2所示。同时由文献［5⁃7］可知，在基础激励下三弹簧准零刚度隔振系统的动力学方程可以用不含线性项的Duffing方程近似表示为：

（25）

由此得到无量纲表达式为：

（26）

其中：。

式中，k₁和k₃分别为系统中线性弹簧和非线性弹簧的刚度；c_l为系统中的线性阻尼。

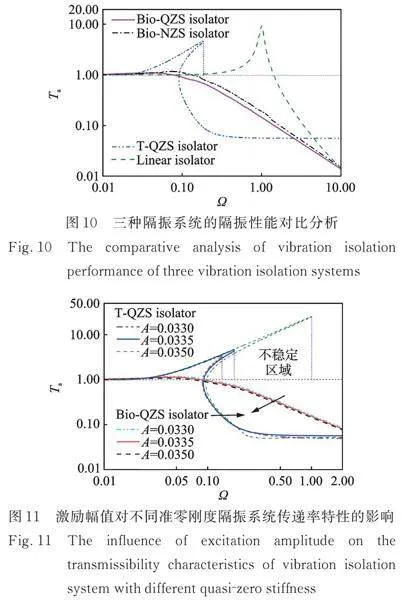
图10中对比分析了在相同负载质量、线性刚度及线性阻尼的条件下施加相同的基础位移激励的仿生肢状准零刚度隔振系统、三弹簧准零刚度隔振系统和线性隔振系统的位移传递率特性。图11中进一步对比分析了不同位移激励幅值对仿生肢状准零刚度隔振系统和三弹簧准零刚度隔振系统位移传递率特性的影响规律（图中用Bio⁃QZS isolator，Bio⁃NZS isolator，T⁃QZS isolator和Linear⁃QZS isolator分别代表仿生肢状准零刚度隔振器、仿生肢状近零刚度隔振器、典型三弹簧准零刚度隔振器和线性隔振器，图11中箭头方向代表位移激励幅值增大的方向）。

由图10可知，相比线性隔振系统，仿生肢状准零刚度隔振系统和典型三弹簧准零刚度隔振系统均具有较低的谐振频率和较宽的隔振频带，有效提高了系统的低频隔振性能。但典型三弹簧准零刚度隔振系统的刚度硬化现象明显，并在跳升和跳降频率区间内存在不稳定区域，极易造成隔振系统失稳现象的发生；相比典型三弹簧准零刚度隔振系统，仿生肢状准零刚度隔振系统在准零刚度区间内具有更低的谐振频率，更小的传递率幅值，同时不存在由跳跃现象导致系统发生失稳，而且即使进入近零刚度区间，虽然谐振频率和传递率幅值均有所增加，但隔振系统依旧具有良好的隔振性能和系统稳定性。

由图11可知，随着位移激励幅值的增大，典型三弹簧准零刚度隔振系统的刚度硬化现象更加严重，这将导致系统不稳定区间增加，有效隔振频带变窄，隔振性能大幅降低。激励幅值的变化对仿生肢状准零刚度隔振系统的位移传递率影响较小，甚至随着激励幅值的增加，系统起始隔振频率有所减小，传递率峰值会进一步降低。因此，仿生肢状准零刚度隔振系统克服了传统准零刚度隔振系统随激励幅值增加系统隔振性能下降的缺陷，能够在较宽的频率范围内有效抑制大幅值的振动，适用于更为复杂多变的工作环境。

4 试验研究

4.1 试验装置及工作原理

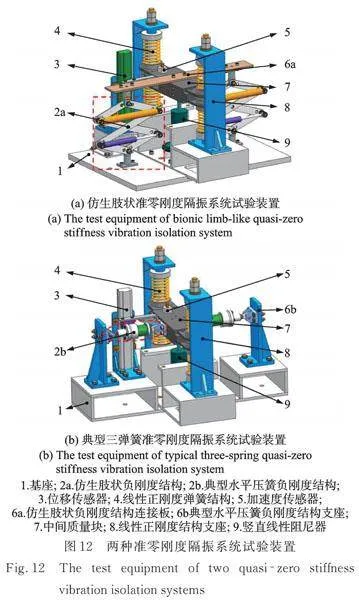
为了验证仿生肢状准零刚度隔振系统的隔振特性及与典型三弹簧准零刚度隔振系统进行对比研究，按照表2中的参数设计了图12中所示的两种试验装置。两种准零刚度隔振试验装置均主要由基座、负刚度结构（仿生肢状负刚度结构或典型水平压簧负刚度结构）、线性正刚度弹簧结构（该装置采用了双压簧正刚度结构，这种结构能够使系统具有更稳定的振动，从而使试验结果更加准确）、中间质量块，竖直线性阻尼器和传感器（分别采用位移传感器和加速度传感器采集中间质量块上的位移信号和加速度信号）等几部分组成。

采用本单位的低频液压振动试验系统进行振动试验研究。试验系统基本参数为：最大推力100 kN，正弦扫频范围0.1～160 Hz，随机扫频最高可达300 Hz。液压振动试验系统主要由油源系统、动力系统、测控系统、振动台面和风冷系统等几部分组成。试验测试的工作原理为：首先安装好试验装置并在测控软件上设置目标谱（振动输入参数），然后由动力系统驱动伺服缸带动试验台面按照目标谱进行振动，最后通过位移传感器、加速度传感器采集实时振动信号传输到测控系统和数据采集系统，用于实时信号监测和数据记录，最终完成振动试验测试工作。

4.2 振动试验与结果分析

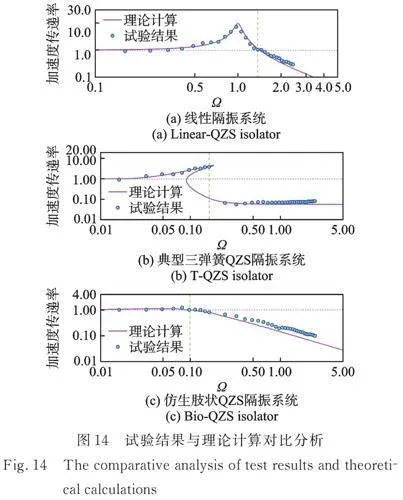
为了能够验证第2节中仿生肢状准零刚度隔振系统动力学模型的准确性，并进一步与第3节的线性隔振系统和典型三弹簧准零刚度隔振系统进行对比分析，采用图13（b）中的低频液压振动测试系统分别对线性隔振系统（图13（a）中准零刚度隔振系统中去掉负刚度结构）、仿生肢状准零刚度隔振系统和典型三弹簧准零刚度隔振系统的试验装置施加正弦激励载荷进行定频振动试验，频率范围为0.1～15 Hz，在0.1～1 Hz的频率间隔为0.1 Hz，1～15 Hz的频率间隔为0.5 Hz。同时通过加速度传感器分别采集每个频率下中间质量块和基座上的加速度时域信号，进一步获得无量纲的加速度传递率，即稳定状态下中间质量块上的加速度幅值与基座上的加速度幅值之比，以便与理论计算进行比较。图14（a）～（c）为三种隔振系统的试验结果与理论计算的对比图。

由图14（a）～（c）可以看出，试验数据与理论计算具有较好的一致性，这说明第2节、第3节中的理论计算模型均能很好地反映出每种隔振系统真实的振动特性规律。由图14（a）可知，线性隔振系统的试验数据与理论计算均在无量纲频率比Ω=1附近出现共振峰值，在Ω=1.4附近进入振动隔离区；由图14（b）可知，典型三弹簧准零刚度隔振系统随着频率比增大，试验数据同样出现了刚度硬化并在最高点出现了跳降现象，虽然跳降频率要低于线性系统的振动隔离频率，但系统存在不稳定状态。由图14（c）可知，相比（a）、（b）中的隔振系统，仿生肢状准零刚度隔振系统在Ω=0.1附近便进入了振动隔离区，具有更小的谐振峰值和更宽的隔振频带，而且不会出现刚度硬化和非线性跳跃现象，系统具有更高的稳定性。同时由14（a）～（c）得到，起始隔振频率比之前的大部分试验数据点落在了理论计算曲线的下方；起始隔振频率比之后的大多数试验数据点落在了理论计算曲线上方，并随着频率比增大有上升趋势，这种现象是试验装置各部件相对运动产生的摩擦阻尼造成的，可以通过润滑的方式减小摩擦阻尼对试验结果造成的影响。

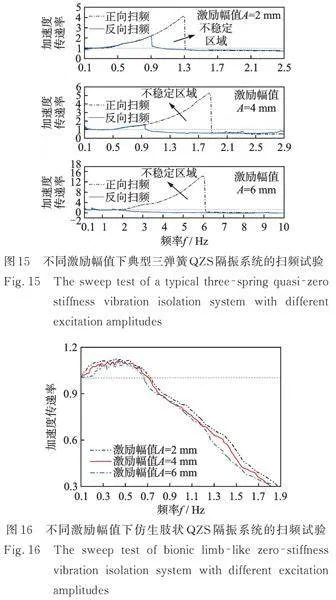
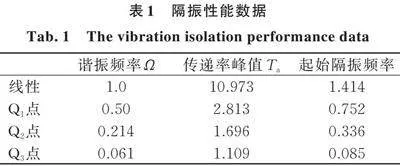
为进一步开展激励幅值变化对仿生肢状准零刚度隔振系统和典型三弹簧准零刚度隔振系统振动特性的对比试验研究，采用低频液压振动试验台分别进行了激励幅值为2、4、6 mm的正反双向扫频试验研究，试验结果如图15和16所示（由于前面研究得到仿生肢状准零刚度隔振系统近似线性系统，单向和双向扫频结果一致，因此图16中只绘制了正向扫频结果）。

由图15可知，通过正反双向扫频试验，典型三弹簧准零刚度隔振系统出现了明显的刚度硬化和非线性跳跃现象，并且随着激励幅值的增加，跳降频率增大，不稳定区域增加，隔振频带变窄，系统隔振性能下降。

由图16可知，通过正向扫频试验，仿生肢状准零刚度隔振系统具有较低的加速度传递率幅值和较小的隔振起始频率，并且随着激励幅值的增加，加速度传递率曲线变化不大，甚至谐振峰值和起始隔振频率有所降低，因此仿生肢状准零刚度隔振系统不仅具有更低的隔振频率，更宽的隔振频带，而且对激励幅值的变化具有低敏性，保证了系统更高的稳定性，可以用于更加复杂多变的工作环境，具有重要的研究意义与工程价值。

5 结" 论

（1） 对于新型仿生肢状准零刚度隔振系统，当其他参数一定，邻边杆长比L_r=1时具有最佳的位移传递率特性，并且通过适当增大初始安装角度和减小连杆长度可以进一步降低系统谐振峰值，提高系统的隔振性能。

（2） 相比线性隔振系统，新型仿生肢状准零刚度隔振系统具有良好的高静低动特性，有效降低了系统的谐振频率，拓宽了其隔振频带，有效提高了系统的隔振性能。

（3） 相比典型的准零刚度隔振系统，新型仿生肢状准零刚度隔振系统不存在刚度硬化和非线性跳跃的现象，具有更高的系统稳定性，而且不会因激励幅值的增加导致系统的隔振性能和稳定性的降低，因此该系统能够在复杂多变的振动环境中保持长期稳定的工作。

（4） 通过定频和扫频的试验研究，不仅验证了新型仿生肢状准零刚度隔振系统理论模型的准确性，而且进一步证明了该准零刚度隔振系统相比线性、典型三弹簧准零刚度隔振系统具有更好的振动隔离性能和系统的稳定性，因此具有重要的研究价值和广阔的应用前景。

参考文献：

［1］""""""" 刘渊博，李明，何琳. 船用气囊隔振系统的非线性动力学特性［J］. 船舶力学，2015，19（11）： 1385-1392.

LIU Yuanbo， LI Ming， HE Lin. Nonlinear dynamics of the marine air-bg vibration isolation system［J］. Journal of Ship Mechanics. 2015，19（11）： 1385-1392.

［2］""""""" 刘海超，闫明，冯麟涵. 带限位隔振系统的冲击响应分析［J］. 振动与冲击，2019，38（21）：172-177.

LIU Haichao，YAN Ming， FENG Linhan， et al. Shock response of a vibration isolation system with displacement restrictors［J］. Journal of Vibration and Shock， 2019， 38（21）：172-177.

［3］""""""" 高双，朱翔，谌宗琦，等. 基于欧拉梁的准零刚度隔振系统动力特性分析［J］. 中国机械工程，2016，27（21）：2869-2876.

GAO Shuang， ZHU Xiang， SHEN Zongqi， et al. Analyses on dynamics characteristics of a quasi-zero-stiffness vibration isolation system based on Euler beam［J］. China Mechanical Engineering，2016，27（21）： 2869-2876

［4］""""""" LI B Y， SHUAI C G， XU W， et al. Review on low frequency control of quasi-zero stiffness［C］//2021 13th International Conference on Computer and Automation Engineering （ICCAE）. Melbourne Australia， 2021：59-63.

［5］""""""" CARRELLA A， BRENNAN M J， WATERS T P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic［J］. Journal of Sound and Vibration， 2007， 301（3-5）： 678-689．

［6］""""""" CARRELLA A， BRENNAN M J， KOVACIC I， et al.On the force transmissibility of a vibration isolator with quasi-zero-stiffness［J］. Journal of Sound and Vibration， 2009， 322（4-5）： 707-717.

［7］""""""" CARRELLA A， BRENNAN M J， WATERS T P， et al.Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness［J］. International Journal of Mechanical Sciences，2012，55（1）： 22-29.

［8］""""""" 赵权，李韶华，冯桂珍. 一种准零刚度车载隔振系统的设计与试验研究［J］.振动与冲击，2021，40（6）：55-63.

ZHAO Quan， LI Shaohua， FENG Guizhen. Design and test of a quasi-zero-stiffness vehicle vibration isolation system［J］. Journal of Vibration and Shock， 2021，40（6）： 55-63.

［9］""""""" LIU X T， HUANG X C， HUA H X. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector［J］.Journal of Sound and Vibration， 2013，332（14）： 3359-3376.

［10］""""" HUANG X C， LIU X T， SUN J Y， et al. Vibration isolation characteristics of a nonlinear isolator using Euler buckled beam as negative stiffness corrector： a theoretical and experimental study［J］.Journal of Sound and Vibration， 2014，333： 1132-1148.

［11］""""" HUANG X C， LIU X T， SUN J Y， et al. Effect of the system imperfections on the dynamic response of a high-static-low-dynamic stiffness vibration isolator［J］. Nonlinear Dynamics， 2014，76：1157-1167.

［12］""""" HUANG X C， CHEN Y， HUA H X， et al. Shock isolation performance of a nonlinear isolator using Euler buckled beam as negative stiffness corrector： theoretical and experimental study［J］.Journal of Sound and Vibration， 2015，345： 178-196.

［13］""""" 利云云，周徐斌，陈卫东，等. 一类双层高静低动刚度隔振系统动力学特性和应用局限性研究［J］. 振动工程学报，2021，34（2） ：364-371.

LI Yunyun， ZHOU Xubin， CHENG Weidong， et al. Dynamic characteristics and application restrictions of a two-stage vibration isolation system with high-static-low-dynamic stiffness［J］. Journal of Vibration Engineering， 2021，34（2）： 364-371.

［14］""""" ZHOU J X， WANG X L， XU D L， et al. Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam-roller-spring mechanisms［J］. Journal of Sound and Vibration，2015，346： 53-69.

［15］""""" WANG X L， ZHOU J X， XU D L， et al. Force transmissibility of a two-stage vibration isolation system with quasi-zero stiffness［J］. Nonlinear Dynamics，2017，87： 633-646..

［16］""""" AHN H J， LIM S H， PARK C.An integrated design of quasi-zero stiffness mechanism［J］. Journal of Mechanical Science and Technology， 2016，30： 1071-1075.

［17］""""" YAO Y H， LI H G， Li Y， et al. Analytical and experimental investigation of a high-static-low-dynamic stiffness isolator with cam-roller-spring mechanism［J］. International Journal of Mechanical Sciences，2020，186：105888.

［18］""""" SUN X T， JING X J. Analysis and design of a nonlinear stiffness and damping system with a scissor-like structure［J］. Mechanical Systems and Signal Processing，2016，66-67： 723-742.

［19］""""" DAI H H， CAO X Y， JING X J， et al. Bio-inspired anti-impact manipulator for capturing non-cooperative spacecraft： theory and experiment［J］. Mechanical Systems and Signal Processing，2020，142：106785.

［20］""""" JIANG G Q， JING X J，GUO Y Q. A novel bio-inspired multi-joint anti-vibration structure and its nonlinear HSLDS properties［J］. Mechanical Systems and Signal Processing，2020，138：106552.

第一作者： 刘海超（1992—），男，博士研究生。E-mail： liu_hc_9206@163.com

通信作者： 闫" 明（1978—），男，博士，教授。E-mail： yanming7802@163.com

基金项目："国防科技创新特区项目（20-163-00-TS-006-002-01）；国家自然科学基金资助项目（51705337）