周期波纹夹芯结构动力学解析建模及振动特性分析

摘要： 本文基于动刚度方法建立了一种周期波纹夹芯结构的动力学解析模型。该模型将耦合结构解耦为若干开口圆柱壳和矩形板，并基于Kirchhoff薄板理论和Flügge薄壳理论推导了对边简支条件下子结构的动刚度矩阵。根据耦合边界处的位移连续性条件和力平衡条件，得到了子结构的坐标转换矩阵，并采用类似于有限元的思想组装了周期结构的全局动刚度矩阵。基于组装的全局动刚度矩阵，计算了三种类型周期波纹夹芯结构的振动特性，并将计算结果与有限元软件ANSYS仿真数据进行对比。研究结果表明，本文建立的解析模型能够在较少的自由度下获得准确的计算结果。此外，还探究了不同夹芯类型和几何参数对周期波纹夹芯结构振动特性的影响。

关键词： 波纹夹芯结构； 振动特性； 动刚度方法； 解析模型

中图分类号： V214.3⁺5； TB532""" 文献标志码： A""" 文章编号： 1004-4523（2025）01-0019-10

DOI：10.16385/j.cnki.issn.1004-4523.2025.01.003

Dynamic analytical modeling and vibration characteristics analysis of periodic corrugated sandwich structures

LI Zhibing， JIN Guoyong， YE Tiangui， YANG Tiejun， CHEN Yukun

（College of Power and Energy Engineering， Harbin Engineering University， Harbin 150001， China）

Abstract： This paper presents a dynamic analytical model of periodic corrugated sandwich structures by using the dynamic stiffness （DS） method. In the model， the coupled structure is decoupled into several open cylindrical shells and rectangular plates， and then based on Kirchoff’s thin plate theory and Flügge’s thin shell theory， the DS matrices of substructures under the condition of simply supported on the opposite side are derived. According to the continuity condition and equilibrium conditions on the coupling boundary， the coordinate transformation matrix of each substructure is derived， and the global DS matrices of the periodic structure are assembled using a similar strategy to the finite element method （FEM）. Based on the assembled global DS matrices， the vibration characteristics for the three types of periodically corrugated sandwich structures are calculated， and the results are compared with those from FEM solutions. The results show that the presented model can obtain accurate calculation results with fewer degrees of freedom. In addition， the effects of different core styles and geometric parameters on the band gap characteristics of the periodic sandwich structure are also explored.

Keywords： corrugated sandwich structure；vibration characteristics；dynamic stiffness method；analytical model

波纹夹芯结构以其轻质、高强度和耐腐蚀等优点被广泛应用于飞机、汽车、船舶等各种工程结构。在实际运用中，该结构的振动是影响其强度和可靠性的关键因素。振动可能导致材料性能下降、疲劳损伤和结构破裂等问题，从而对使用安全构成潜在威胁。因此，对波纹夹芯结构的动力学特性进行研究具有重要意义。

近年来，国内外学者对波纹夹芯结构的动力学特性进行了大量的研究。SHU等^［1］运用Castigliano定理和等效均质理论提出了一种用于预测三角形波纹板弯曲性能的方法。袁文昊等^［2］基于Hamilton变分原理建立了不同边界条件下的波纹板动力学模型，并采用指数剪切变形理论分析了材料和几何参数对其振动特性的影响。随后，李凤莲等^［3］建立了四边简支下的波纹夹芯板的动力学方程，并探究了不同夹芯结构的声振特性。LIU等^［4］基于非线性几何关系和Hamilton变分原理建立了石墨烯增强复合材料波纹板的非线性动力学方程，并探究了几何尺寸对其振动特性的影响。李锁斌等^［5］通过引入超材料提出了一种超结构夹芯板，并基于有限元方法探究了其带隙特性，结果表明所建立的超材料波纹板具有良好的力学承载和低频带隙特性。XIA等^［6］从实验、数值和理论三个方面研究了波纹夹芯板在沿其中心线方向施加纵向载荷时的力学响应。LIU等^［7］ 通过试验和有限元仿真分析深入研究了U型波纹夹芯板在准静态压缩载荷下的变形机理，并推导了U型波纹夹芯板变形抗力的解析公式。李震等^［8］采用微分求积有限元方法建立了由多个圆弧壳组成的波纹板的动力学模型，随后，基于前期的研究，他们又探究了新型波纹夹芯板结构在各种边界条件下的振动特性^［9］。

从以上文献可知，目前对波纹夹芯结构的动力学特性研究主要基于有限元方法和等效介质理论。虽然等效介质理论可以简化数学模型，但它忽略了波纹板内部复杂的结构和材料不均匀性，对模型的精确度和可靠性有一定的影响。有限元方法虽然对模型具有很强的适应性，但在处理大型结构和高频计算时，往往需要将结构划分成足够小的单元，这会导致巨大的计算量并对计算机性能有更高的要求。鉴于此，本文采用动刚度方法建立了对边简支条件下周期波纹夹芯结构的动力学精确解析模型。在本模型中首先将耦合结构划分为若干开口圆柱壳和矩形板，并基于相应的控制微分方程获得其在对边简支条件下的精确位移解。然后，根据边界处位移和力的关系推导出各子结构的动刚度矩阵，并根据耦合边界处的位移连续性和力平衡条件，得到了子单元的坐标变换矩阵。接着，采用与有限元方法类似的策略组装了周期波纹夹芯结构的全局动刚度矩阵。最后，基于建立的解析模型，计算了三种不同波纹夹芯结构的振动特性，并将计算结果与有限元软件ANSYS的仿真结果进行对比。同时，探究了不同夹芯类型和几何参数对周期波纹夹芯结构振动特性的影响。

1 模型介绍

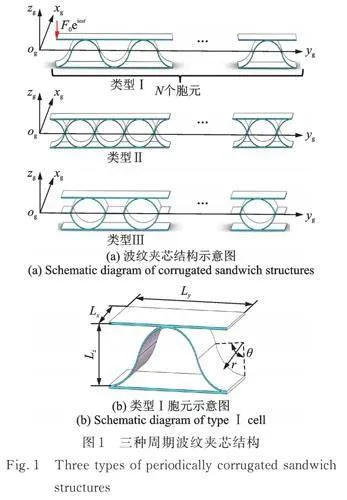
本研究建立的周期波纹夹芯结构如图1（a）所示，整个周期结构由多个胞元沿着y_g方向相互耦合而成。图1（b）给出了其中一种胞元结构，其由开口圆柱壳和矩形板组成，其中L_x、L_y、L_z是胞元在不同方向上的长度，θ和r分别为开口圆柱壳的圆心角和半径。在本研究中假设矩形板和开口圆柱壳都为均匀的、各向同性的弹性材料，且都具有相同的厚度，并忽略转动惯量和剪切效应的影响，故分别采用Kirchhoff薄板理论和Flügge薄壳理论进行动力学建模。

1.1 子结构动力学模型

1.1.1 矩形板

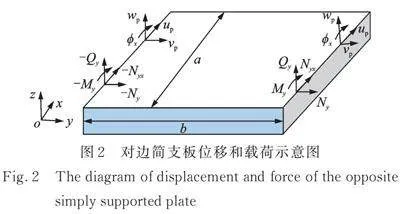
首先，建立矩形板的动力学模型，其位移和载荷如图2所示。在本研究中，将同时考虑板的横向和面内振动，并假设板在x=0和x=a上处于简支支撑（v_p=w_p=0）。根据Kirchhoff薄板理论，在小变形范围内，板的横向和面内振动控制微分方程可以解耦为^{［10⁃11］}：

（1）

式中，分别为矩形板不同方向的位移；为圆频率；为板的弯曲刚度；；；，E_p为板的弹性模量；ρ_p为板的密度；υ_p为板的泊松比；h_p为厚度。

矩形板的位移与力和力矩的关系为^{［10⁃11］}：

（2）

式中，和分别为矩形板内对应方向的面内剪力；和为横向剪力和弯矩。

简支边界条件下，板的位移解可以表示为：

（3）

式中，m表示板单元在x方向上的波数；M为三角级数项数；分别为矩形板在y方向的位移分量。将式（3）代入方程（1）可得到如下的位移解析解：

（4）

式中，c_i为未知系数；r_i为特征方程的4个根。将式（4）得到的位移解析解代入式（2）便可得到矩形板力和力矩的解析表达式。

沿着边界线y=0和y=b的位移和载荷可以表示为：

（5）

（6）

式中，上标“in”和“out”分别代表板面内和横向振动；。结合式（3）～（6）及载荷和位移的关系，可得到如下矩阵：

（7）

（8）

式中，分别为与波数m相关的矩形板边界位移和载荷组成的矩阵，其维度为4M×4M。通过式（5）～（8），可以得到矩形板的动力学方程为：

（9）

式中，为板的面内/横向动刚度矩阵。

板完整的动力学方程可表示为：

（10）

式中，

（11）

其中每个子矩阵的维度为2M×2M。

1.1.2 开口圆柱壳

接下来，将建立开口圆柱壳的动力学方程，其位移和载荷如图3所示。在本研究中，假设开口圆柱壳两曲边 （α=0，α=L）为简支支撑（v_s=w_s=0）。基于Flügge 薄壳理论，开口圆柱壳的振动控制微分方程为^［12］：

（12）

式中，，，分别为开口圆柱壳不同方向的位移。

（13）

式中，，h_s为厚度；系数A_i （i=1，2，3，4，5，6，7，8，9，10）的详细表达式见文献［12］。

开口圆柱壳的位移与力和力矩的关系为^［12］：

（14）

式中，为开口圆柱壳的弯曲刚度；，分别为开口圆柱壳的弹性模量和泊松比。

简支边界条件下，开口圆柱壳的位移解可以表示为^［12］：

（15）

式中，m代表开口圆柱壳单元在α方向上的波数；为三角级数项数；分别为开口圆柱壳在β方向的位移分量。

将式（15）代入式（12）便可得到开口圆柱壳的位移解析解如下：

（16）

式中，p_i （i=1，2，3，4，5，6，7，8） 为特征方程的根；δ_i、γ_i为将U_s.m和V_s.m用W_s.m表示时的系数；为未知系数。

将式（16）代入式（14）便可得到开口圆柱壳的力和力矩的解析解。与板单元类似，沿着边界线β=θ和β=0的位移和载荷可以表示为：

（17）

式中，。结合式（14）～（17）及载荷和位移的关系，可得到如下矩阵：

（18）

式中，分别为与波数m相关的开口圆柱壳边界位移和载荷组成的矩阵，其维度为8M×8M。通过式（17）～（18），可以得到开口圆柱壳的动力学方程为：

（19）

式中，为开口圆柱壳动刚度矩阵，其维度为8M×8M。

1.2 耦合结构动力学模型

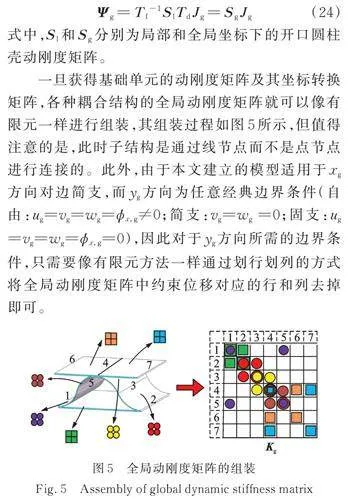
为了建立耦合结构的整体动力学方程，需将开口圆柱壳和矩形板的动刚度矩阵从局部坐标系转换到统一的全局坐标系下。在本研究中，选取以开口圆柱壳的圆心为原点的笛卡尔坐标系作为整体结构的全局坐标系（如图4所示），对于图1所示的波纹夹芯结构，由于其上下面板与所建立的全局坐标系在同一平面，因此对于矩形板单元，无需进行坐标变换。若芯层由矩形板组成，仅需进行类似于文献［13］描述的坐标变换即可。此外，在组装全局动刚度矩阵和进行坐标变换之前，应先对矩形板和开口圆柱壳的动刚度矩阵进行排序，具体排序过程可参考文献［13］。

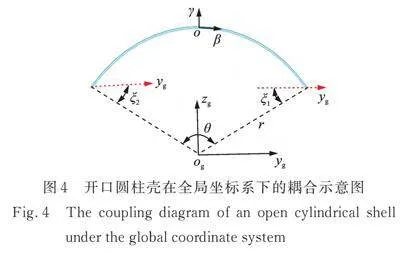
图4给出了开口圆柱壳在全局坐标下的几何关系示意图，其中ξ₁和ξ₂为开口角连线与全局坐标y_g正方向之间的夹角，当其在z_g正方向为正，反之为负。根据耦合边界上的位移连续性条件和平衡条件，可得到如下关系矩阵^［14］：

（20）

式中，分别表示局部坐标下开口圆柱壳的位移和载荷向量；分别表示全局坐标下开口圆柱壳的位移和载荷向量。

（21）

（22）

（23）

式中，右上角上标数字代表开口圆柱壳边界；I、I_cosξ，I_sinξ分别为对角线元素为1、cosξ和sinξ的对角矩阵，且维度均为M×M。

结合式（20）～（23），全局坐标下的开口圆柱壳的动力学方程可以表示为：

（24）

式中，和分别为局部和全局坐标下的开口圆柱壳动刚度矩阵。

一旦获得基础单元的动刚度矩阵及其坐标转换矩阵，各种耦合结构的全局动刚度矩阵就可以像有限元一样进行组装，其组装过程如图5所示，但值得注意的是，此时子结构是通过线节点而不是点节点进行连接的。此外，由于本文建立的模型适用于x_g方向对边简支，而y_g方向为任意经典边界条件（自由：u_g=v_g=w_g=≠0；简支：v_g=w_g =0；固支：u_g=v_g=w_g==0），因此对于y_g方向所需的边界条件，只需要像有限元方法一样通过划行划列的方式将全局动刚度矩阵中约束位移对应的行和列去掉即可。

在研究周期结构的振动特性时，需要考虑外部载荷的施加，由于夹芯结构外部载荷主要作用于上下面板，故本研究只考虑外部载荷作用于面板的情况。对于外部载荷，一般有两种载荷形式，一种是点载荷，一种是线载荷，具体表达式如下：

点载荷：

（25）

线载荷：

（26）

式中，F₀、M₀分别为外部简谐力和的幅值。

2 数值算例

为了验证本文建立模型的准确性，对图1所示的三种胞元进行自由振动分析。为了方便计算，所有开口圆柱壳和矩形板均采用相同的厚度和材料参数，包括弹性模量E=210 GPa、密度ρ=7800 kg/m³、泊松比υ=0.3和厚度h=0.003 m，且所有壳和板的尺寸分别相同，除非特殊说明。三种胞元的整体尺寸分别为L_x=0.3 m，L_y=0.2828 m，L_z=0.0586 m，其中所有开口圆柱壳的尺寸为r=0.1 m，θ=45°，L=0.3 m，耦合角度ξ_i有两种情况，分别为90°和45°，对应不同的坐标系方向有不同的值，具体可见图4。对于类型Ⅲ胞元，芯层中板的宽度L_y=0.0707 m。 此外，值得注意的是，本文给出的所有算例边界条件均为x_g方向两端简支约束，而y_g方向全自由。

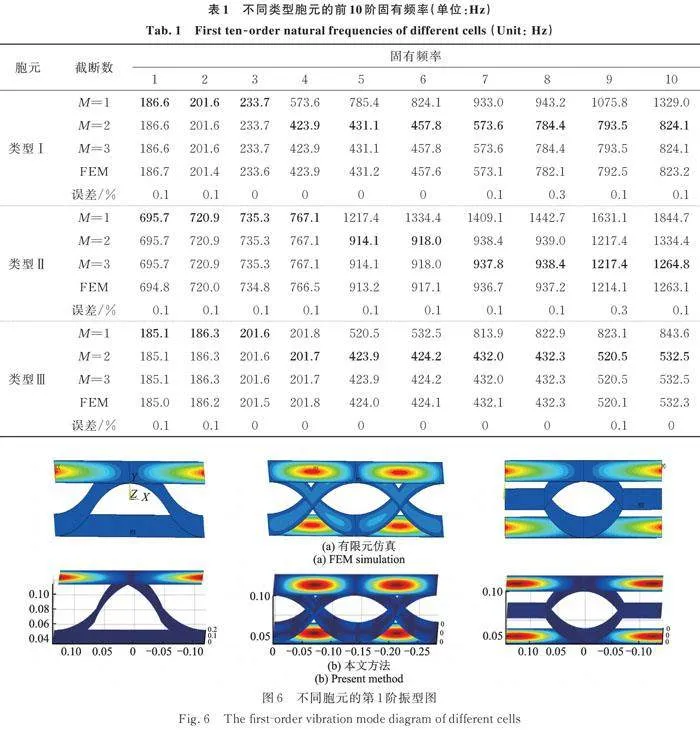
表1给出了对边简支条件下不同类型胞元的前10阶固有频率，其中有限元结果采用ANSYS仿真软件计算得到。在有限元仿真中，单元类型采用SHELL63，单元尺寸为0.01×0.01 m²，该网格尺寸已满足收敛性要求。从表1可以看出，所建立的模型具有良好的收敛性（粗体表示收敛值），并且计算结果与有限元仿真结果基本相同。此外，图6展示了本文方法和有限元软件绘制的不同类型胞元的第1阶振型图。从中不难发现，两种方法绘制的振型图吻合良好，进一步验证了本文建立模型的正确性。

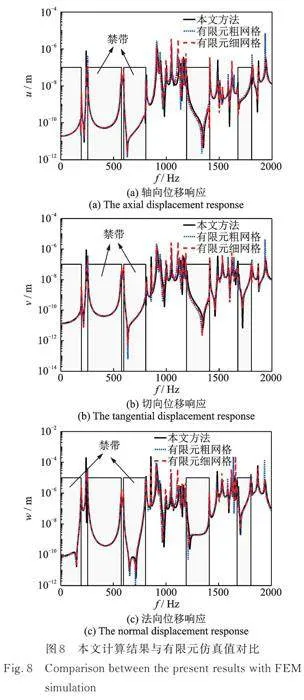
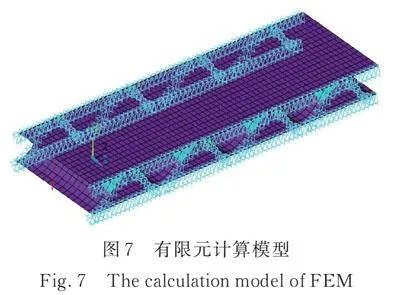
为了进一步验证本文提出方法的正确性，分别采用本文方法和有限元仿真软件ANSYS对图1所示的类型Ⅰ周期结构进行谐响应分析。在本次计算中，模型的整体尺寸为：0.3 m×1.1312 m×0.0586 m，由4个类型Ⅰ胞元组成，其有限元计算模型如图7所示。点载荷F=10e^iωt作用于最左侧边界中点（0.15， 0， 0.0586） m，响应提取位置为最右测边界点（0.05， 1.1312，0.0586） m，如图1（a）所示。在ANSYS中，采用SHELL63单元，并分别采用（0.015×0.015） m²粗网格和（0.01×0.01） m²细网格进行求解。当使用粗网格时，整个结构需要5120个单元和5250个节点，而使用细网格时，达到11040个单元和11222个节点，可见，在有限元方法中网格数量是巨大的，而本文方法只需要使用28个动刚度单元和22个线节点。图8对比了两种方法的计算结果，从中可以看出，三条曲线的整体趋势吻合良好，且细网格的计算结果更接近本文结果。此外，从图8中可以发现，在0～2000 Hz范围内有5个较明显的禁带（灰色区域），这些禁带主要由周期结构对弹性波或振动的反射和折射效应引起，当振动或弹性波传播到周期性结构表面时，根据Bragg定律，弹性波会被散射回去或者在结构内部被反射和折射，当波长与周期结构的间距相适应时，散射和反射将不断增强，使得特定频率范围内的振动和弹性波无法传播，从而形成Bragg带隙。

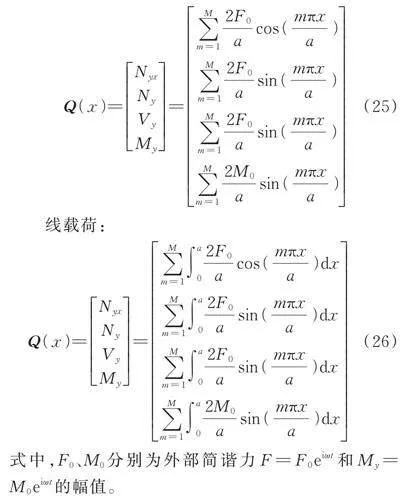
如前文所述，周期波纹夹芯结构主要生成Bragg带隙，而这种带隙通常受到结构几何参数的影响。接下来，将研究不同的几何和材料参数以及夹芯类型对周期结构带隙特性的影响。值得注意的是，在接下来的研究中，计算模型的材料和几何参数与前文的谐响应分析时相同，除非另有说明。首先，探究不同厚度对带隙特性的影响。在本次研究中，假定上下面板和芯层具有相同的厚度，并分别选取0.002，0.003和0.004 m。图9给出了不同厚度下周期波纹板结构的频率响应曲线。从图9中可以观察到，不同厚度的周期波纹结构的禁带位置和谐振频率变化明显，随着板厚的增加，周期夹芯结构的带隙越来越明显。因此，若要充分利用周期结构的带隙特性以实现所需的隔振效果，结构的厚度是一个值得考虑的重要因素。

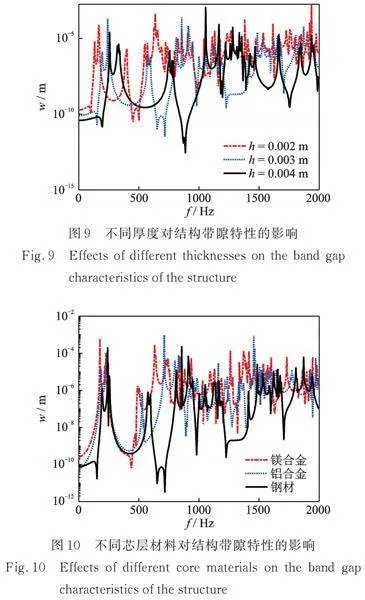
周期结构的带隙特性不仅取决于其几何参数，还受到材料特性的影响。为了探究不同材料对整体结构带隙的影响，在本次研究中假定夹芯结构的上下面板采用钢材，这是因为钢材具有较高的强度和刚度，能够提供足够的支撑和保护，而芯层材料分别选取钢材、镁合金和铝合金，其中，镁合金的材料参数为E=45 GPa，ρ=1800 kg/m³，υ=0.35；铝合金的材料参数为E=79 GPa，ρ=2800 kg/m³，υ=0.33，厚度均为0.003 m。图10给出了不同芯层材料下周期结构的频响曲线。通过对比，可以观察到钢材芯层具有最宽的带隙。这意味着钢材能够更有效地限制波在结构中的传播。相比之下，镁合金芯层的带隙相对较小，其限制波传播的效果较差。铝合金芯层的带隙介于镁合金和钢材之间，因此芯层材料对周期结构的影响也是不可忽略的。

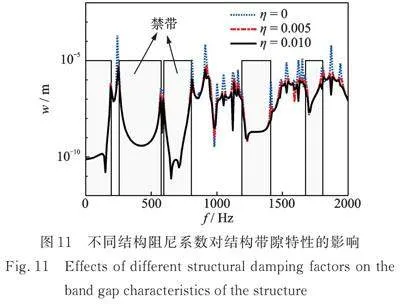
接下来探究结构阻尼对带隙特性的影响。在周期波纹结构中，结构阻尼可以通过选择不同的材料、调整结构设计等方式来实现。在此次计算中，采用复杨氏横量来描述结构阻尼的影响，阻尼系数η分别设置为0、005和0.01。图11展示了周期结构在不同结构阻尼水平下的频响曲线。从中可以发现，结构阻尼并不会影响结构的禁带数目和范围，但随着结构阻尼的增加，共振峰值会明显降低。因此，在设计周期波纹板的面板和夹芯时，应根据实际应用情况，选择适当的结构阻尼。

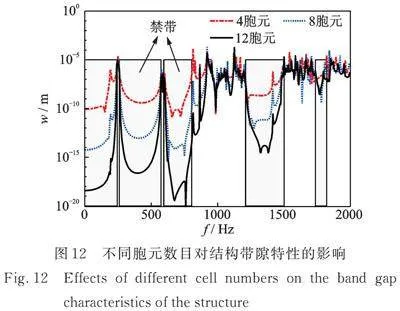
此外，胞元数目也是影响Bragg带隙的重要因素。图12展示了沿y_g方向不同胞元数目时周期结构的带隙特性曲线。通过观察可以发现，由于胞元的几何和材料参数相同，不同胞元数目的周期结构具有相同的禁带位置。然而，随着胞元数目的增加，禁带内的响应下降得更为显著，这意味着禁带中的波在结构中传播更加困难。通常情况下，通过增加胞元数目可以增加周期结构的复杂性，并增强材料的非均匀性，从而扩大带隙的范围。然而，需要注意的是，胞元数目越多并不一定意味着带隙越明显，因为周期结构的带隙特性还取决于结构的材料和几何参数等其他因素。

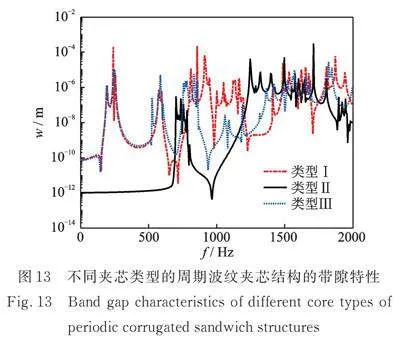
芯层是波纹夹芯结构中不可或缺的一部分，它可以引入额外的振动模态并影响结构的带隙特性。不同类型的夹芯会影响周期结构的频率响应函数，并对带隙特性产生不同的影响。例如，水平型连通的夹芯可以提高结构的剪切刚度，从而引入新的振动模态，并扩大带隙范围。在这种类型的夹芯中，上下面板通过夹芯角连接起来，形成类似于梁的结构，从而增强了结构的剪切刚度。相反，采用更柔软的泡沫夹芯可以减小结构的剪切刚度，并降低结构的共振频率，从而缩小带隙宽度。因此，接下来将分析图1中的三种不同形状夹芯结构的带隙特性，其中所有板和开口圆柱壳均采用前文所述的材料参数（钢材），且三种类型的结构整体长度均为0.3 m×1.1312 m×0.0586 m，对于类型Ⅲ，芯层中板的长度L_y=0.0707 m。图13展示了不同夹芯类型的周期波纹夹芯结构的带隙特性，可以看出在0～2000 Hz范围内，类型Ⅱ结构的带隙特性最为显著，这是因为类型Ⅱ结构具有更多的开口圆柱壳单元，增强了反射声波或振动的能力，相比之下，类型Ⅰ和类型Ⅲ的带隙特性不怎么明显，究其原因是其壳体单元较少，间隔较大，使得声波和振动容易穿透。

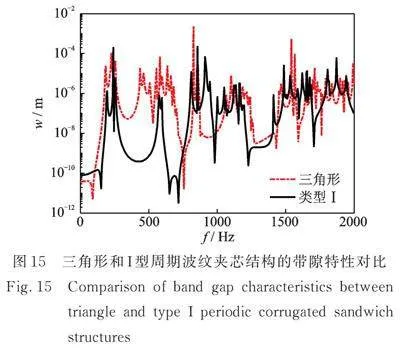
为了深入研究夹芯类型对结构带隙特性的影响，本文还构建了一个由矩形板夹芯组成的三角形周期夹芯结构，如图14所示。该结构的整体尺寸与前文研究中相同，即0.3 m×1.1312 m×0.0586 m，中间夹芯板的尺寸为0.3 m×0.1531 m，板与板之间的夹角为22.51°。图15展示了三角形周期夹芯结构和前文建立的类型Ⅰ周期夹芯结构的频率响应曲线。在计算过程中，仍然采用钢材材料，并保持激励力大小、激励位置、响应位置以及约束条件与之前的研究相同。从图15中可以观察到，在给定的频段内，类型Ⅰ波纹板具有更宽的禁带，表明它能更有效地抑制振动。然而，三角形波纹板具有更简单的结构和便于制造的优势，因此在实际应用中，应根据具体需求和约束条件选择适当的结构形式。

3 结 论

本文基于动刚度方法建立了由开口圆柱壳和矩形板组成的周期夹芯结构的通用解析模型。首先详细推导了子结构动刚度矩阵，并阐述了耦合结构全局动刚度矩阵的组装过程和外部载荷的处理方法。接着，基于建立的解析模型计算了三种类型的周期波纹夹芯结构的振动特性，并将计算结果与有限元仿真值进行比较。结果表明，所建立的解析模型能够在较少自由度下获得准确的计算结果。此外，还探究了周期结构几何、材料参数以及夹芯类型对结构带隙特性的影响。研究结果表明，增加结构的厚度有利于周期结构获得更宽的带隙，而增加胞元数目也会导致带隙宽度的增加。此外，随着夹芯类型的变化，带隙宽度也会发生变化。结构阻尼对结构的禁带数目和范围没有明显影响，但随着结构阻尼的增加，共振峰值会显著降低。总之，这项研究为波纹夹芯结构的理论建模提供了思路和方法，为周期波纹夹芯结构的设计和优化提供了理论参考。

参考文献：

［1］""""""" SHU C F， HOU S J. Theoretical prediction on corrugated sandwich plates under bending loads［J］. Acta Mechanica Sinica， 2018， 34（5）： 925-935.

［2］""""""" 袁文昊， 李凤莲， 吕梅. 不同边界条件下波纹夹芯板的自由振动特性［J］. 复合材料学报， 2020， 37（12）： 3149-3159.

YUAN Wenhao， LI Fenglian， LYU Mei. Free vibration characteristics of corrugated sandwich plates under different boundary conditions［J］. Acta Materiae Compositae Sinica， 2020， 37（12）： 3149-3159.

［3］""""""" 李凤莲， 袁文昊， 吕梅. 梯形和三角形波纹夹芯板的声振特性研究［J］. 振动工程学报， 2022， 35（2）： 514-526.

LI Fenglian， YUAN Wenhao， LYU Mei. Vibro-acoustic characteristics of trapezoidal and triangular corrugated sandwich plates［J］. Journal of Vibration Engineering， 2022， 35（2）： 514-526.

［4］""""""" LIU Y F， QIN Z Y， CHU F L. Nonlinear free vibration of graphene platelets reinforced composite corrugated plates［J］. Journal of Central South University， 2022， 29（9）： 3054-3064.

［5］""""""" 李锁斌， 魏儒义， 周安安，等. 超结构夹芯板及其低宽频振动带隙机理［J］. 西安交通大学学报， 2021， 55（4）： 77-85.

LI Suobin， WEI Ruyi， ZHOU Anan， et al. A new sandwich type metamaterial plate and its mechanism of low-frequency broad vibration band gap［J］. Journal of Xi’an Jiaotong University， 2021， 55（4）： 77-85.

［6］""""""" XIA F K，YU T X， DURANDET Y， et al. Triangular corrugated sandwich panels under longitudinal bending［J］. Thin-Walled Structures， 2021， 169： 108359.

［7］""""""" LIU K， ZONG S， LI Y， et al. Structural response of the U-type corrugated core sandwich panel used in ship structures under the lateral quasi-static compression load［J］. Marine Structures， 2022， 84： 103198.

［8］""""""" 李震， 钟锐， 秦斌， 等. 波纹板结构动力学建模及其自由振动特性分析［J］. 计算力学学报， 2023，40（4）：568-575.

LI Zhen， ZHONG Rui， QIN Bin， et al. Analysis on dynamic modeling and free vibration characteristics of corrugated plate structure［J］.Chinese Journal of Computational Mechanics， 2023，40（4）：568-575.

［9］""""""" LI Z， QIN B， WANG Q S， et al. Vibration behavior analysis of novelty corrugated-core sandwich plate structure by using first-order shear deformation plate and shell theories［J］. The European Physical Journal Plus， 2022， 137： 270.

［10］""""" BANERJEE J R， PAPKOV S O， LIU X， et al. Dynamic stiffness matrix of a rectangular plate for the general case［J］. Journal of Sound and Vibration， 2015， 342： 177-199.

［11］""""" NEFOVSKA-DANILOVIĆ M， PETRONIJEVIĆ M. In-plane free vibration and response analysis of isotropic rectangular plates using the dynamic stiffness method［J］. Computers amp; Structures， 2015， 152： 82-95.

［12］""""" KOLAREVIĆ N， NEFOVSKA-DANILOVIĆ M. Dynamic stiffness-based free vibration study of open circular cylindrical shells［J］. Journal of Sound and Vibration， 2020， 486： 115600.

［13］""""" ZHANG C Y， JIN G Y， YE T G， et al. Harmonic response analysis of coupled plate structures using the dynamic stiffness method［J］. Thin-Walled Structures， 2018， 127： 402-415.

［14］""""" LI Z B， JIN G Y， YE T G， et al. A unified vibration modeling of open cylindrical shell-rectangular plate coupling structures based on the dynamic stiffness method［J］. Journal of Sound and Vibration， 2023， 563： 117870.

第一作者： 李直兵（1996―），男，博士研究生。E-mail：zhibingli@hrbeu.edu.cn

通信作者： 靳国永（1980―），男，博士，教授。E-mail：guoyongjin@hrbeu.edu.cn

基金项目："国家自然科学基金资助项目（5225109，52241101，52271309）；黑龙江省优秀青年科学基金资助项目（YQ2022E104）