风浪联合作用下驳船型海上浮式风机的非线性耦合模型与TMD振动控制研究

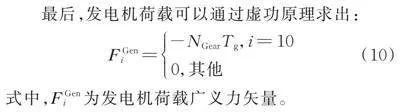
摘要： 海上浮式风机是捕获深远海风能的重要装置，是风能开发的主要研究方向之一。驳船型风机多采用二维低阶简化动力学模型和非线性最小二乘参数识别方法，建立高阶耦合动力模型能更准确地反映其动力特性。本文关注驳船型海上浮式风机的多体系统，建立风浪联合作用下的16自由度耦合动力学模型，通过数值仿真验证模型的准确性。其中，利用修正的叶素动量理论计算叶片气动荷载，利用线性势流理论计算波浪荷载，采用准静态法计算系泊张力。此外，为减小驳船型海上浮式风机的结构振动，在考虑发电机转矩控制和叶片集体变桨控制的基础上，提出将双向碰撞调谐质量阻尼器置于机舱中，并引入限位装置控制振子行程。随后，通过穷举法和遗传算法进行控制参数优化。仿真分析表明，本文所建模型可准确计算驳船型海上浮式风机的动力响应；双向碰撞调谐质量阻尼器对结构振动有较好的控制效果。

关键词： 振动控制； 驳船型海上浮式风机； 非线性耦合模型； 双向TMD； 风浪联合作用

中图分类号： TB535； TK83""" 文献标志码： A""" 文章编号： 1004-4523（2025）01-0008-11

DOI：10.16385/j.cnki.issn.1004-4523.2025.01.002

Nonlinear coupled model and TMD vibration control of barge-type" floating offshore wind turbine under combined wind and wave action

KONG Fan^1，2， CHEN Lingshuang¹， ZHENG Dacheng¹， LI Shujin¹， DONG Hua³

（1.School of Civil Engineering and Architecture， Wuhan University of Technology， Wuhan 430070， China；2.College of Civil Engineering， Hefei University of Technology， Hefei 230009， China；3.China Construction Third Bureau First Construction Engineering Co.， Ltd.， Wuhan 430080， China）

Abstract： Capable of capturing offshore wind energy， the floating wind turbine is one of the primary research interests for researchers in the wind energy community. Researchers usually adopt two-dimensional low-degree-of-freedom simplified planar models for offshore barge-type wind turbines， where the model parameters are identified by the nonlinear least square method. In this case， the accuracy of these models depends highly on parameter fitting. Given the unique structure of offshore floating wind turbines and the surrounding environment， a multi-degree-of-freedom coupled dynamical model is necessary to yield more realistic dynamic behaviors. In this paper， we present a coupled dynamic model with 16 degrees of freedom for the multi-body system of barge-type offshore floating wind turbines under the combined action of wind and waves. The model accuracy is verified through numerical simulation using OpenFAST， developed by the National Renewable Energy Laboratory （NREL）. In particular， the modified Blade Element Momentum theory is used to calculate the blade aerodynamic load， the linear potential flow theory is used to determine the wave load， and the quasi-static method is used to obtain the tension of the mooring systems. Besides the generator torque control and blade pitch control， a bi-directional tuned mass damper （TMD） is placed in the nacelle to mitigate the structural vibration of the floating wind turbine of the barge‑type， where a limiting device is introduced to limit the TMD stroke. Subsequently， the control parameters are optimized by the method of exhaustion and the genetic algorithm. The simulation analyses show that the model proposed in this paper accurately alculates yields the dynamic response of the barge-type offshore floating wind turbine. The bi-directional TMD with collision mechanism is efficient in mitigating the structural response.

Keywords： vibration control；barge-type floating offshore wind turbine；nonlinear coupled model；bi-directional TMD；combined wind and wave action

海洋蕴含丰富的风能资源，具有风力稳定、风速大的特点。远海风能利于大规模风电开发，是未来风电行业的主要发展方向之一^［1‑2］。海上浮式风机是一种捕获远海风能的发电装置。然而，海洋复杂的风浪环境作用会使浮式风机产生较大位移，使风机系统负荷增加，可使用性能降低^［3］。桨距控制能有效降低风机响应，但目前针对浮式风机的多数研究未考虑变速和变桨控制；此外，桨距控制的减振作用通常以增加桨距作动器的使用、降低风机功率稳定性以及增大结构疲劳载荷为代价^［4‑6］。因此，国内外学者将土木工程领域中的振动控制方法应用到风机中，以减小风机系统响应并保证风机正常工作。

调谐质量阻尼器（tuned mass damper， TMD）作为常见的结构振动控制手段^［7‑8］，在海上浮式风机的减振控制中效果显著。LACKNER等^［9］将TMD设置在静水无风的驳船（barge）型浮式风机机舱中，通过在仿真工具OpenFAST中加入结构控制模块来研究风机振动控制响应；经过工程经验的初步优化，发现控制效果仅达到10%。STEWART等^［10］为不同类型浮式风机建立了3自由度（DOF）动力学模型；将TMD放入机舱或平台中，利用最小二乘法拟合模型未知参数；研究发现塔架疲劳损伤降低了5%～20%。HE等^［11］对驳船型海上风机配置了机舱TMD，建立三自由度简化模型；由于机舱空间有限，引入了限位装置。YANG等^［12］根据拉格朗日方程建立驳船型风机的3‑DOF简化模型；将TMD置于其底部平台，并优化了控制参数和控制效果。LI等^［13］通过FAST模拟单桩和驳船型风机模型，并对比了TMD与主动控制的减振效果。

综上所述，目前多采用二维平面简化动力学模型模拟驳船型浮式风机，忽略了叶片、塔架和平台之间的耦合效应。此外，模型还需利用非线性最小二乘法识别结构和环境荷载参数，因此，模型适用性依赖参数拟合精度。上述两个原因极大地限制了简化模型的应用范围。也有学者直接利用FAST控制模块模拟风机减震试验^［14］，但这只适用于FAST已集成的控制装置。若要研究其他控制装置的减振效果，则要对FAST进行二次开发，从而导致工作量加大。因此，为更真实地计算风机振动响应，须建立多自由度的耦合模型^［15］。值得注意的是，目前多数研究将转子转速视为定值，并使发电功率保持恒定，忽略了发电机、叶片和系统间的耦合效应，从而限制了上述研究的适用性^{［16‑17］}。本文以美国可再生能源实验室（National Renewable Energy Laboratory， NREL）的5 MW驳船型海上浮式风机为研究对象，考虑发电机转矩控制和叶片集体变桨控制的影响，以便更好地描述环境荷载下转子转速和发电功率的变化，并在此基础上研究双向TMD的控制效果。

1 驳船型风机模型

1.1 模" 型

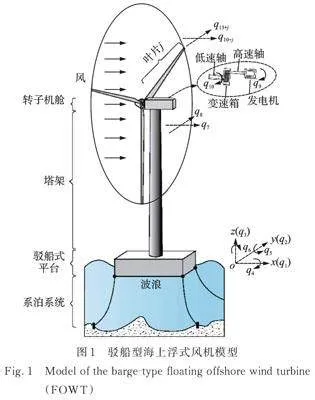
本节建立驳船型海上浮式风机的16‑DOF耦合模型。风机系统中的平台、机舱和轮毂视为刚体，塔架、叶片视为弹性悬臂梁，并忽略它们的轴向变形^［15］。利用准静态法求解浮式风机的系泊荷载^［18］，即任意时刻的系泊都处于静平衡状态，通过悬链线方程得到系泊张力。值得注意的是，根据文献［15］，作用在浮式风机塔架上的气动荷载远小于叶片气动荷载，因此本文忽略风荷载对塔身的影响。另外，本文不再赘述系泊荷载的计算过程，具体推导可参考文献［18‑19］。

图1为驳船型海上浮式风机的16‑DOF模型示意图，表1列出了其具体参数。图中，对应平台的6个自由度，即横荡、纵荡、垂荡、横摇、纵摇和艏摇；分别为塔架纵向和侧向振动；分别为三叶片的摆振向（flapwise）和挥舞向（edgewise）振动。此外，为更好地描述传动系的作用以及模拟风机发电功率的变化，本文考虑了传动系旋转‑柔性自由度和发动机自由度。

1.1.1 坐标系

为描述驳船型海上浮式风机的运动特征，本文分别在平台、塔架、机舱、轮毂和叶片处建立局部坐标系，以定义各构件的位置信息。取初始时刻平台中轴线与静水面的交点为原点建立惯性坐标系，用于定义平台6个自由度。在局部坐标系上定义结构参数，然后通过旋转变换矩阵实现局部坐标系到惯性坐标系的转换，并进一步建立运动方程。

对于欧拉角（，，），可根据欧拉角转换公式^［20］求得绕三轴旋转的坐标变换矩阵为分别。参考坐标系xyz转动角度，其位置可通过下式表示：

（1）

式中，。

此外，用于计算系统动能的角速度可通过变换矩阵得到：

（2）

式中，为欧拉角速度与角速度的变换矩阵。建立坐标系后，可得到位置矢量的表达式；进而，对位置矢量求时间导数得到速度矢量；最后，求解风机系统的动能和势能。

1.1.2 运动方程

本节通过欧拉‑拉格朗日方程推导barge型海上浮式风机运动方程：

（3）

式中，T为系统动能；V为系统势能；为广义坐标；为对时间求导；分别为系统的气动力、静水力、水动力、系泊荷载和发电机荷载；为系统阻尼矩阵。

由于浮式风机系统的非线性，其质量矩阵和刚度矩阵过于复杂，不具体列出。利用四阶龙格‑库塔法直接对运动方程进行求解^{［15，21］}。

1.2 荷" 载

驳船型海上浮式风机受到的环境荷载主要包括：系泊的定位约束作用、波浪和海流等产生的水动力荷载、湍流风导致的气动荷载以及发电机荷载。本文计算作用于驳船型浮式风机的环境荷载，并通过虚功原理计算广义力。

1.2.1 水动力荷载

通过谱表现法，选用JONSWAP波高谱，模拟海上随机波高：

（4）

式中，为频率；为有效波高；为谱峰周期；为不规则海况的峰型参数；为比例因子。

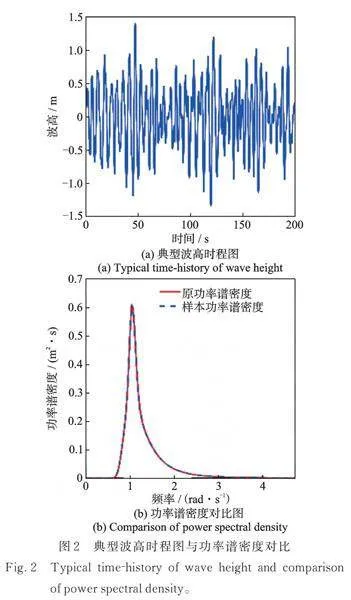
取有效波高，谱峰周期，模拟时长，利用谱表现法^［22］模拟典型波高时程图，如图2（a）所示；图2（b）对比了原目标功率谱与样本功率谱估计值，验证模拟所得波高时程样本的集合特征。

采用JONKMAN^［18］提出的线性势流理论计算波浪荷载。该法结合了势流理论和莫里森（Morison）方程，利用势流理论计算波浪力和辐射力，利用莫里森方程计算黏滞阻力。水动力荷载广义力矢量可表示为：

（5）

式中，为波浪绕射力；为卷积积分时间的代数；为黏滞阻力；表示静水刚度矩阵；为结构附加阻尼和质量导致的水动力；为海水密度；g为重力加速度；为平台静止时的排量；为克罗内克函数。

1.2.2 气动力荷载

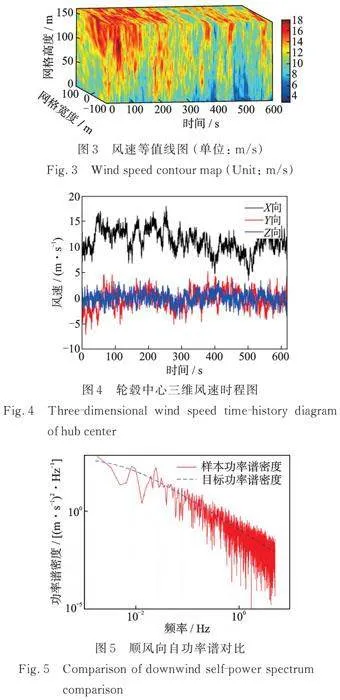
风速样本由平均风和脉动风的风速叠加形成。本文采用指数率确定平均风速，选择Kaimal谱模拟脉动风速。图3为NREL提供的TurbSim生成的以轮毂为中心的二维风速场。随后，利用泰勒冻结湍流假设（Taylor’s frozen turbulence hypothesis）^{［23‑24］}生成三维风速时程，用以准确描述叶片与风场之间的耦合效应。图4所示为轮毂中心处三个方向的风速时程图（X为迎风向；Y、Z为横风向），图5为顺风向相应的自功率谱对比图。然而，浮式风机在风浪作用下易发生较大位移，为使运行时的风轮仍能被风场完全覆盖，应生成足够大的风场平面。本文网格宽度取为200 m，网格高度取160 m，轮毂高度处平均风速，风切变指数，叶片转速"r/min。

采用叶素动量（blade element momentum， BEM）理论计算作用在旋转叶片上的空气动力荷载。BEM理论中存在的一些假定（如圆盘假设）会导致计算精度降低，因此许多学者提出Glauert、 Prandtl修正模型使计算值更精确^［25］。本文利用普朗特叶尖损失因子（Prandtl’s tip loss factor）弥补叶片数量无限的缺陷，考虑格劳特校正（Glauert correction）修正轴向感应系数大于0.4时的失效情况。修正后叶片的法向力和切向力可通过下式计算^［26］：

（6）

（7）

式中，为空气密度；为入流风与叶片的相对速度；为弦长；分别为法向和切向系数。求解得到和后，将气动荷载转换到惯性坐标系中，通过虚功原理计算广义气动力矢量。

1.2.3 发电机荷载

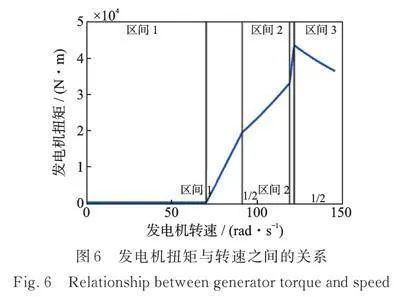
本文通过引入传动系旋转‑柔性自由度和发动机自由度考虑变速控制和叶片桨距控制对驳船型海上浮式风机的影响。根据JONKMAN^［18］的建议，采取恒功率的发电机转矩控制策略。图6反映了5个工作区的过渡关系^［18］：

（8）

式中，和分别为发电机扭矩和转速。注意到式（8）中的小数进行了舍入。

由于驳船型浮式风机的平台尺寸较大，叶片变桨和平台变桨运动之间会产生耦合^［26］，产生负阻尼效应。因此，本文采用LARSEN等^［27］修正过的叶片集体变桨控制，其桨距角的计算可表示为：

（9）

式中，为变化的桨距角值；为低速与额定转速的差值；为高速转轴与低速转轴的转速比。分别为桨距控制的比例、积分和导数增益，详见文献［28‑29］。

最后，发电机荷载可以通过虚功原理求出：

（10）

式中，为发电机荷载广义力矢量。

1.3 模型验证

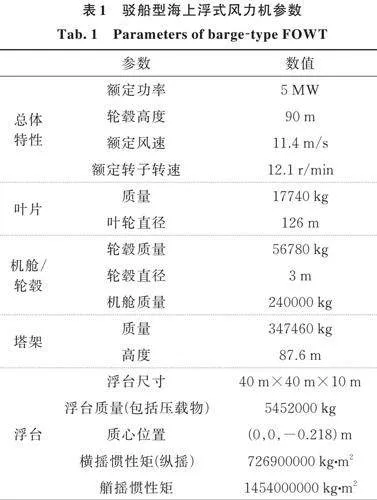
以驳船型海上浮式风机为研究对象，机舱和轮毂重296780 kg，叶片长度61.5 m，重17740 kg，平台尺寸为40 m×40 m×10 m，浮台质量（包括压载物）重5452000 kg。

根据美国国家海洋和大气管理局（National Oceanic and Atmospheric Administration， NOAA）海上浮标的数据显示，风浪荷载常存在大量的偏角，这种风浪失调会导致风机出现前后和侧向的振动^［30］。由于海上浮式风机在侧向的结构阻尼很小，且与转子推力在前后方向提供的空气动力阻尼正交，所以错位波会增加支撑结构^{［31‑32］}的整体荷载。因此，假定风浪偏角为30°，可更好地考虑风浪荷载的耦合作用，贴合真实的风浪条件。

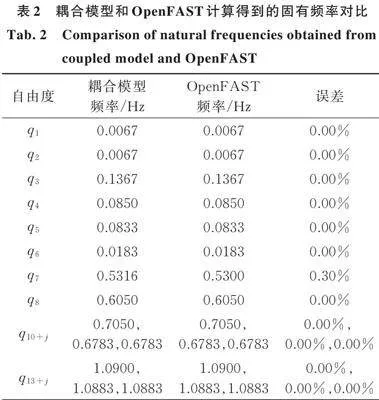
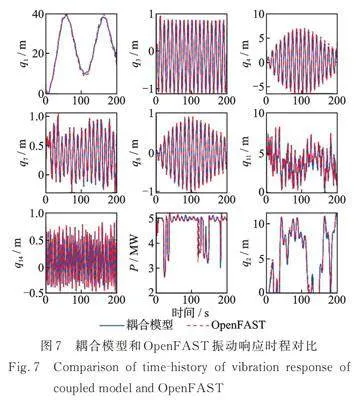
在上述环境荷载作用且风机正常运行情况下，可由1.1节给出的运动微分方程得到驳船型海上浮式风机的16‑DOF耦合响应。通过分析静水无风情况下各个自由度的自由振动，对所得的时程曲线作快速傅里叶变换（FFT），从而求得系统各个自由度的固有频率，表2对比了静水无风条件下耦合模型和OpenFAST计算得到的固有频率，可见耦合模型能精确模拟浮式风机的动力特性。图7对比了耦合模型计算得到的结构若干自由度上的振动响应时程以及发电机功率P和OpenFAST模型所得相应结果，可见两种模型所得结果吻合甚好。综上所述，本文提出的16‑DOF耦合模型正确且有效，能准确计算各自由度的振动响应，为振动控制研究奠定基础。

2 控制装置模型

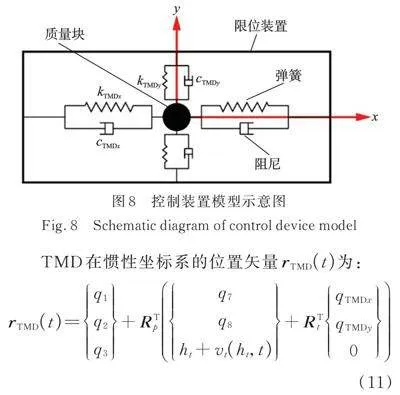
将TMD放置于机舱内以控制驳船型风机的振动，图8为双向TMD控制装置模型示意图。双向TMD模型由质量块和正交方向的弹簧阻尼系统组成，在机舱局部坐标系中定义TMD两个正交方向自由度，建立18‑DOF包含双向TMD的驳船型海上浮式风机结构动力学模型。

TMD在惯性坐标系的位置矢量为：

（11）

则双向TMD的动能和势能可分别表示为：

（12）

（13）

式中，为双向TMD的质量；为双向TMD的速度矢量，由位置矢量对时间求导可得；为双向TMD的刚度；、为双向TMD的阻尼；为TMD在惯性坐标系中的方向分量，用于表征TMD的重力势能。将式（12）和（13）求得的动能和势能代入式（3）即可计算和双向TMD控制下的18‑DOF系统耦合响应。

机舱的尺寸约为^［12］，TMD可使用空间非常有限。此外，风浪作用下的TMD行程较大，易与浮式风机主结构发生碰撞，从而影响风机结构安全^［33］。此外，由于驳船型风机主频较低，为达到更好的控制效果，TMD常调谐至较低频率，这会导致振子产生较大冲程。因此，为防止TMD与机舱发生直接碰撞，有必要设置限位装置。作为算例，将TMD纵向（x方向）限制为，侧向（y方向）限制为。采用FAST的限位模型^［34］，它类似于线性黏弹性碰撞模型，其碰撞力为：

（14）

式中，为碰撞刚度；为碰撞阻尼；为碰撞过程中的相对变形；和分别TMD纵向和侧向允许的最大和最小位移。

3 TMD参数优化

将双向TMD置于机舱内，研究控制效果。风机结构采用16‑DOF驳船型风机耦合模型，TMD采用第2节所述的双向带限位装置的模型。根据VILLOSLADA^［35］使用的TMD质量比，选择机舱中TMD的振子质量为40000 kg。

3.1 穷举法

在计算效率允许的情况下，本文采用穷举法（采用TMD不同刚度和阻尼的组合）计算塔架振动位移的标准差，并找到最优控制参数。双向TMD的刚度区间取为"，阻尼区间取为"。此外，双向TMD中限位装置的刚度和阻尼依据文献［35］分别取为"N/m和"。图9为不同刚度与阻尼下塔架纵向和侧向位移响应的标准差，最优控制刚度和阻尼如表3所示。此时，x方向TMD的最优频率（0.52 Hz）与塔架纵向振动基频（0.53 Hz）接近，具有较优的控制效果；对于y方向，TMD最优频率（0.22 Hz）与塔架侧向振动基频（0.61 Hz）和平台横摇频率（0.083 Hz）均相差较远。出现这种情况的原因可能是TMD质量块在y向发生频繁碰撞导致的。图10为双向TMD控制下振子最大行程图，由于y向限位作用，TMD振子与结构发生碰撞，导致控制频率与结构主频相差较大。

图11（a）和（b）分别为TMD参数（刚度和阻尼）与塔顶纵向和侧向位响应移标准差的等值线图。图中，颜色越深代表塔顶位移标准差越小，减振效果越好。对比图11（a）和（b）可见，x方向TMD的鲁棒性明显优于y方向，TMD参数偏离x方向最优刚度和阻尼时，仍能获得较好控制效果。反之，在y方向的低刚度和阻尼处，全局最优值附近会出现多处局部最优值；而较高刚度和阻尼处曲面平滑。显然，这是由于刚度和阻尼较低时，振子更容易与限位装置产生碰撞造成的。穷举法计算量较大，进而本文采用遗传算法优化双向TMD的控制参数。

3.2 遗传算法

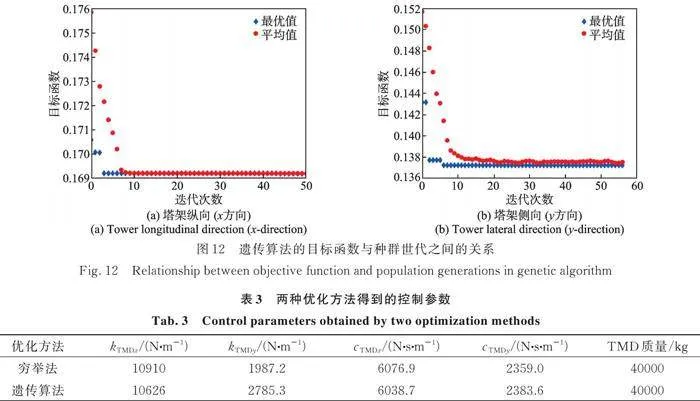
遗传算法（genetic algorithm， GA）的参数设置如下：寻优范围与穷举法相同，采用50个个体的种群规模，交叉概率为0.8，突变函数符合高斯分布，采用塔架机舱处位移标准差为目标函数，算法的目的为使目标函数值最小。GA的目标函数与种群世代之间的关系如图12所示。由图12可见，10代左右时，x方向最优个体的目标函数值即可达到平均值。这表示GA仅需要评价目标函数500次左右即能得到最优参数，相较穷举法，GA的计算效率有大幅提高。y方向上，GA收敛速度较x方向慢，直到第20代左右，种群目标函数平均值才接近最优值；世代数增加并不能使种群平均值达到个体最优值。显然，这是由于y方向上TMD参数存在多处局部最优导致的，与上文穷举法提到的结论相符。穷举法和GA得到最优参数如表3所示，两种计算方法得到的优化参数差异在2%以内，但y方向上的刚度参数差异较大。这是由于穷举法所设间隔不够小，从而搜索不到GA所得最优值，可见GA能准确有效地优化控制参数。对于存在局部最优的y方向，遗传算法能更快地找到全局最优。

4 结果分析

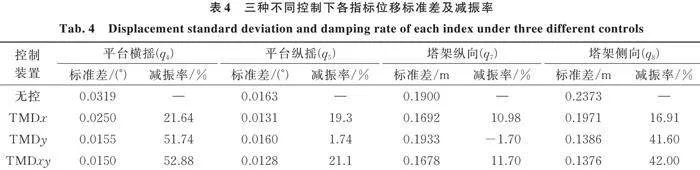
图13（a）～（d）为驳船型风力发电机在有/无双向TMD控制下的结构振动位移时程图，分别反映了双向TMD在平台横摇、平台纵摇、塔架纵向（）和塔架侧向（）自由度上的减振效果。由图13可见，放置在机舱中的双向TMD对浮式风机塔架和平台的振动均有很好的控制作用。双向TMD从开始工作到发挥稳定控制作用，塔架和平台振幅明显减小，并保持在一定幅度范围内。取4个自由度的位移响应标准差为评价指标：双向TMD控制下平台横摇位移标准差为0.0150 m，相对无控减少了52.88%；平台纵摇位移标准差为0.0128，达到了21.1%的控制效果；塔架纵向和侧向位移标准差分别为0.1678和0.1376，分别达到了11.7%和42.0%的控制效果。图13（e）～（f）为双向TMD控制下振子行程图，虚线表示挡板位置。可见限位后的行程满足机舱内使用空间要求。此外，挡板使振子运动轨迹发生改变，耗散了部分能量。

对比平面内/外双向TMD的控制效果可以发现，平台纵摇和塔架侧向振动的减振作用明显优于平台横摇和塔架纵向振动。可能是由于在建模过程中考虑了叶片的桨距控制，而它能一定程度上减小x方向振动。另外，有研究^［36］发现，风浪方向的不一致性和波流相互作用都可能进一步激发平面内风机的振动，而本文为模拟真实的风浪条件，假设风浪偏角为30°。综上所述，双向TMD在y方向的振动控制作用更明显。

频域上的振动控制效果体现得更加明显。图14（a）～（d）为平台横摇、平台纵摇、塔架纵向位移、塔架侧向位移响应的功率谱密度（power spectral density， PSD）。由图14（a）和（b）可见，平台横摇和纵摇只有一个主频，塔架对平台的影响较小；由图14（c）和（d）可见，塔架纵、侧向位移均有两个主频，表明平台对塔架位移响应影响较大。此外，在双向TMD控制下，平台和塔架PSD曲线的峰值均明显减小。比较无控和受控情况下PSD曲线覆盖的面积可知，风机平台横摇、纵摇和塔架纵向、侧向振动的能量分别减少了64.99%、36.63%和23.23%、46.32%。无论控制前后，塔架振动能量均集中于低频（平台）处，且控制装置的能量削减作用也主要集中于低频。在塔架纵向自由度上，控制后低频对应的峰值约为高频的3.02倍；在塔架侧向自由度上，控制后低频处峰值约为高频的6.65倍。在塔架纵向和侧向自由度上，低频比高频减振率分别提高了68.83%和61.26%。由此可见，平台是影响塔架振动的重要原因，双向TMD对平台和塔架位移均能起到较好的抑制作用。图14（e）和（f）分别为叶片摆振向、挥舞向位移的功率谱密度图。由于叶片振动主要由气动荷载导致，与塔架耦合的效应不大，置于机舱内部的双向TMD对叶片减振效果不明显。

上述分析说明双向TMD发挥了可观的平台和塔架减振作用。此外，表4列出了机舱放置两种单向TMD和双向TMD装置时，平台和塔架两个方向振动的位移标准差及减振率， 此时单向TMD采用双向TMD中对应的最优参数。由表4可知，尽管单向TMD对结构振动有一定控制效果，但仅布置单向TMD对另一方向的振动控制效果不明显。例如，只在y方向布置TMD甚至会增大塔架纵向位移。由此可见，双向比单向TMD对结构振动的控制作用更充分全面，效率更高。

5 结" 论

（1）建立了风浪联合作用下驳船型风机的16‑DOF耦合动力模型：采用考虑普朗特叶尖损失因子和格劳特校正的叶素动量理论计算叶片气动荷载，利用线性势流理论和莫里森方程计算波浪荷载，利用准静态法计算系泊张力，并引入发电机转矩控制和叶片集体变桨控制。通过与仿真软件OpenFAST对比，验证了所建模型的正确性。

（2）基于16‑DOF耦合动力模型验证了双向调谐质量阻尼器的控制效果，并利用穷举法和遗传算法优化了双向TMD的控制参数。在两个方向引入限位装置，防止TMD行程过大。双向TMD对塔架侧向的振动控制效果比纵向更好；双向TMD比单向TMD具有更好的控制效果。

参 考 文 献：

［1］""""""" SHAH K A， MENG F T， LI Ye， et al. A synthesis of feasible control methods for floating offshore wind turbine system dynamics［J］. Renewable amp; Sustainable Energy Reviews， 2021， 151： 111525.

［2］""""""" 罗金平， 喻旭明， 陈杰峰，等.一种海上浮式风电基础频域动力响应分析新技术［J］. 振动工程学报， 2019， 32（2）： 288-295.

LUO J P， YU X M， CHEN J F， et al. A technique of floating wind turbine dynamic response estimation in frequency domain［J］. Journal of Vibration Engineering， 2019， 32（2）： 288-295.

［3］""""""" SALIC T， CHARPENTIER J F， BENBOUZID M， et al. Control strategies for floating offshore wind turbine： challenges and trends［J］. Electronics， 2019， 8（10）： 1185.

［4］""""""" OLONDRIZ J， ELORZA I， JUGO J， et al. An advanced control technique for floating offshore wind turbines based on more compact barge platforms［J］. Energies， 2018， 11（5）： 1187.

［5］""""""" 唐耀， 范菊， 邹早建，等.浮式风机平台在规则波和定常风作用下的动力响应分析［J］. 中国海洋平台， 2014， 29（1）： 50-56.

TANG Y， FAN J， ZOU Z J， et al. Dynamic response analysis of floating offshore wind turbine platform in regular waves and steady winds［J］. China Offshore Platform， 2014， 29（1）： 50-56.

［6］""""""" 张洪建， 蔡新， 许波峰. 浮式风机半潜式平台动力响应研究［J］. 可再生能源，2021， 39（9）： 1210-1216.

ZHANG H J， CAI X， XU B F. Study on dynamic response of floating wind turbine semi-submersible plateform［J］. Renewable Energy Resources， 2021， 39（9）： 1210-1216.

［7］""""""" 贺辉， 谭平， 刘彦辉，等.圆形高耸结构两级变阻尼TMD风振控制［J］. 振动工程学报， 2020， 33（3）： 503-508.

HE H， TAN P， LIU Y H， et al. Wind-induced vibration control of circular section high-rise structures employing TMD with two-stage damping level［J］. Journal of Vibration Engineering， 2020， 33（3）： 503-508.

［8］""""""" 李亚峰， 李寿英， 陈政清.旋转惯质双调谐质量阻尼器的优化与风振控制研究［J］. 振动工程学报， 2020， 33（2）： 295-303.

LI Y F， LI S Y， CHEN Z Q. Optimization and wind-induced vibration suppression of rotational inertia double tuned mass damper［J］. Journal of Vibration Engineering， 2020， 33（2）： 295-303.

［9］""""""" LACKNER M A， ROTEA M A. Structural control of floating wind turbines［J］. Mechatronics ， 2011， 21（4）： 704-719.

［10］""""nbsp; STEWART GORDON， LACKNER MATTHEW. Offshore wind turbine load reduction employing optimal passive tuned mass damping systems［J］. IEEE Transactions on Control Systems Technology， 2013， 21（4）： 1090-1104.

［11］""""" HE E M， HU Y Q， ZHANG Y. Optimization design of tuned mass damper for vibration suppression of a barge-type offshore floating wind turbine［J］. Proceedings of the Institution of Mechanical Engineers， Part M： Journal of Engineering for the Maritime Environment， 2017， 231（1）： 302-315.

［12］""""" YANG J， HE E M， HU Y Q. Dynamic modeling and vibration suppression for an offshore wind turbine with a tuned mass damper in floating platform［J］. Applied Ocean Research， 2019， 83： 21-29.

［13］""""" LI X W， GAO H J. Load mitigation for a floating wind turbine via generalized H_∞ structural control［J］. IEEE Transactions on Industrial Electronics， 2016， 63（1）： 332-342.

［14］""""" DING Q W， LI C， CHENG S S， et al. Study on TMD control on stability improvement of barge-supported floating offshore wind turbine based on the multi-island genetic algorithm［J］. China Ocean Engineering， 2019， 33（3）： 309-321.

［15］""""" 李书进， 郑达成， 孔凡.海上浮式风机多体系统耦合动力模型研究［J］. 振动工程学报， 2024， 37（1）： 20-30.

LI S J，ZHENG D C， KONG F. Coupled dynamic model of multi-body system of floating offshore wind turbine［J］. Journal of Vibration Engineering， 2024， 37（1）： 20-30.

［16］""""" 刘增辉，陈建兵，宋玉鹏，等.考虑桨叶伺服控制的浮式风机多刚体动力学建模与验证［J］. 振动工程学报， 2023， 36（4）： 892-902.

LIU Z H， CHEN J B， SONG Y P，et al. Modeling and verification of multi-rigid body dynamics of floating offshore wind turbines considering servo control［J］. Journal of Vibration Engineering， 2023， 36（4）： 892-902.

［17］""""" 陈建兵， 宋玉鹏.海上浮式风机的一体化建模及其整体可靠性［J］.空气动力学学报，2022， 40（4）： 191-202.

CHEN J B， SONG Y P. Integrated dynamic modeling and global reliability analysis of floating offshore wind turbines［J］. Acta Aerodymamica Sinica， 2022， 40（4）： 191-202.

［18］""""" JONKMAN J M. Dynamics of offshore floating wind turbines—model development and verification［J］. Wind Energy： An International Journal for Progress and Applications in Wind Power Conversion Technology， 2009， 12（5）： 459-492.

［19］""""" HØEG C， ZHANG Z L. The influence of different mooring line models on the stochastic dynamic responses of floating wind turbines［J］. Journal of Physics： Conference Series， 2018， 1037（6）： 062016.

［20］""""" FOSSEN T I. Handbook of Marine Craft Hydrodynamics and Motion Control［M］. United Kingdom： John Wiley amp; Sons Ltd.， 2011.

［21］""""" 孔凡， 夏红兵， 孙超，等.风浪联合作用下海上风力涡轮机的碰撞阻尼减振控制［J］. 振动与冲击， 2021， 40（3）： 19-27.

KONG F， XIA H B， SUN C， et al. Pounding tuned mass damper for vibration control of offshore wind turbine subjected to combined wind and wave excitations［J］. Journal of Vibration and Shock， 2021， 40（3）： 19-27.

［22］""""" SHINOZUKA M， DEODATIS G. Simulation of stochastic processes by spectral representation［J］. Applied Mechanics Reviews， 1991， 44（4）： 191-204.

［23］""""" JONKMAN B J. TURBSIM user’s guide［R］. NREL/TP‑500-39797. Golden， Colorado， USA： National Renewable Energy Laboratory （NREL）， 2006.

［24］""""" PLATT A， JONKMAN B， JONKMAN J. InflowWind user’s guide［EB/OL］. https：//www.nrel.gov/wind/nwtc/assets/downloads/InflowWind/InflowWind_Manual.pdf.

［25］""""" HANSEN M O L. Aerodynamics of Wind Turbines［M］. Sterling， USA： Earthscan， 2015.

［26］""""" NING A， HAYMAN G， DAMIANI R， et al. Development and validation of a new blade element momentum skewed-wake model within AeroDyn［C］//33rd Wind Energy Symposium. Kissimmee， Florida， USA， 2015：20-37.

［27］""""" LARSEN T J， HANSON T D. A method to avoid negative damped low frequent tower vibrations for a floating， pitch controlled wind turbine［J］. Journal of Physics： Conference Series， 2007， 75（1） ：012073.

［28］""""" JONKMAN J M. Dynamics modeling and loads analysis of an offshore floating wind turbine［D］. Boulder： University of Colorado at Boulder， 2007.

［29］""""" HANSEN M H， HANSEN A D， LARSEN T J. Control design for a pitch-regulated， variable speed wind turbine［R］. Risoe National Laboratory ， Roskilde， 2005.

［30］""""" STEWART G M， LACKNER M A.The impact of passive tuned mass dampers and wind‑wave misalignment on offshore wind turbine loads［J］. Engineering Structures， 2014， 73： 54-61.

［31］""""" SUN C， NAGARAJAIAH S， DICK A J. Experimental investigation of vibration attenuation using nonlinear tuned mass damper and pendulum tuned mass damper in parallel［J］. Nonlinear Dynamics， 2014， 78（4）： 2699-2715.

［32］""""" SUN C， NAGARAJAIAH S， DICK A J. Family of smart tuned mass dampers with variable frequency under harmonic excitations and ground motions： closed-form evaluation［J］. Smart Structures and Systems， 2014， 13（2）： 319-341.

［33］""""" 杨佳佳， 贺尔铭， 姚文旭，等. 抑制海上浮式风力机振动的 TMD 限位策略研究［J］. 振动与冲击， 2020， 39（15）： 18-24.

YANG J J， HE E M， YAO W X， et al. TMD limited position strategy for vibration suppression of floating offshore wind turbines［J］. Journal of Vibration and Shock， 2020， 39（15）： 18-24.

［34］""""" LA C W， LACKNER M A. Theory manual for the tuned mass damper module in FAST v8［EB/OL］. https：//www.nrel.gov/wind/nwtc/assets/pdfs/tmd-theory.pdf.

［35］""""" VILLOSLADA D， SANTOS M， TOMÁS-RODRÍGUEZ M. TMD stroke limiting influence on barge-type floating wind turbines［J］. Ocean Engineering， 2022， 248： 110781.

［36］""""" ZHANG Z L， HØEG C. Inerter-enhanced tuned mass damper for vibration damping of floating offshore wind turbines［J］. Ocean Engineering， 2021， 223： 108663.

第一作者：孔" 凡（1984―），男，博士，教授。 E-mail： kongfan@hfut.edu.cn

通信作者： 董" 华（1984―），男，硕士，高级工程师。E-mail： donghua@cscec.com

基金项目：国家自然科学基金面上项目（52078399）