不同极槽配合车用永磁电机多物理场仿真分析

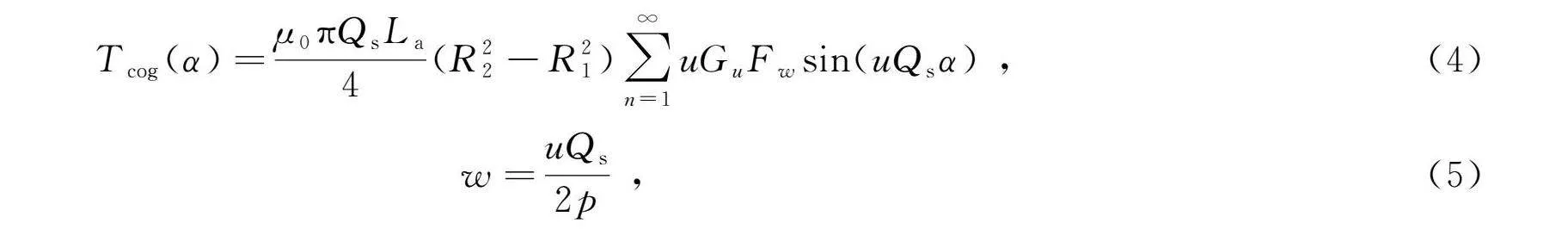
摘 要：针对车用永磁同步电机设计面临的诸多挑战，以8极48槽和8极36槽内置式永磁同步电机为研究对象，研究了不同极槽配合对车用永磁同步电机电磁性能以及振动噪声的影响。首先，比较分析不同极槽配合永磁同步电机的转矩波动、空载反电势，探究不同极槽配合对电机电磁性能的影响；其次，基于麦克斯韦应力张量法推导电磁力波的解析模型，并通过解析模型和有限元模型分别分析不同极槽配合的电机电磁力波的空间阶次和频率特征；最后，建立电机多物理场耦合模型，探究不同极槽配合对永磁同步电机振动噪声的影响。结果表明，8极36槽电机在转矩波动、空载反电势等电磁性能方面要显著优于8极48槽电机，然而，由于其存在较低的空间非零电磁力波，更易引发共振，产生振动噪声。分析结果揭示了不同极槽配合对永磁同步电机电磁性能及电机振动噪声的影响，为电机设计选取极槽配合以及后续优化提供了理论参考。

关键词：电机学；永磁同步电机；极槽配合；电磁性能；振动噪声；电磁力波

中图分类号：TM359.9

文献标识码：A"" DOI：10.7535/hbkd.2025yx01002

收稿日期：2024-08-05；修回日期：2024-10-23；责任编辑：冯民

基金项目：

国家自然科学基金（52305267）；山东省自然科学基金（ZR2022QE116）；山东省精密制造与特种加工重点实验室资助项目（90015322019）

第一作者简介：

李国昊（1998—），男，山东聊城人，硕士研究生，主要从事电动动力系统理论与技术方面的研究。

通信作者：

尹红彬，副教授。E-mail：hbinyin@163.com

Multi physics field simulation analysis of different pole slots

combined with automotive permanent magnet motors

LI Guohao" YIN Hongbin" "SUN Yigang" ZHANG Zhe" BI Xiangjun" HU Wenjing1

（1.School of Traffic and Vehicle Engineering， Shandong University of Technology， Zibo， Shandong 255049， China;

2.China National Heavy Duty Truck Group Company Limited， Jinan， Shandong 25001" China）

Abstract：Aiming at the problems in the design of permanent magnet synchronous motor for vehicles， taking the 8-pole 48-slot and 8-pole 36-slot interior permanent synchronous motors as subject， the influence of different pole-slot combinations on the electromagnetic performance and vibration noise of permanent magnet synchronous motor for vehicles were researched. Firstly， the torque ripples and no-load back electromotive forces of the permanent synchronous motor with different pole-slot combinations were comparatively analyzed in order to investigate the influence of different pole-slot combinations on the electromagnetic performance of the motor. Secondly， the analytical model of electromagnetic force wave was deduced based on Maxwell stress tensor method， and the spatial order and frequency characteristics of the electromagnetic force wave of the motor with different pole-slot combinations were analyzed by the analytical model and the finite element model， respectively. Finally， a multi-physical field coupling model of the motor was established to investigate the effects of different pole-slot combinations on the vibration noise of the permanent magnet synchronous motor. The results show that the 8-pole 36-slot motor is significantly better than the 8-pole 48-slot motor in terms of torque ripple， no-load back electromotive force， and other electromagnetic performances. However， due to the existence of lower spatial non-zero electromagnetic force waves， it is more likely to trigger resonance and generate vibration noise. The analytical results reveal the effects of different pole-slot combinations on the electromagnetic performance and vibration noise of permanent magnet synchronous motors， and provide theoretical references for the selection of pole-slot combinations and subsequent optimization of motor design.

Keywords：electrical machinery; permanent magnet synchronous motor; pole-slot combination; electromagnetic performance; vibration noise; electromagnetic force wave

内置式永磁同步电机以其高效能、高功率密度、宽调速范围等显著优点，被广泛应用于航空航天、机器人、电动汽车领域，特别是在汽车领域，永磁同步电机因其独特的优势，成为车用驱动电机的主要发展方向^[1-2]。然而，随着汽车驱动性能要求的不断提高，如低齿槽转矩、低转矩波动、振动噪声等，永磁同步电机的设计面临诸多挑战。其中，极槽配合作为影响电机性能的关键要素之一，其选择对电机的电磁性能及振动噪声特性具有显著影响。

在电机电磁性能的研究领域内，KIMS^[3]对比分析了8极12槽与8极9槽表贴式电机的特性，明确指出8极9槽电机在高转矩密度和低齿槽转矩方面展现出显著优势，但伴随有径向力不对称及功率因数偏低的问题，为解决这些缺陷，提出了采用多倍极槽数的策略。与此同时，李烽等^[4]针对交替极电机，深入研究了不同极槽配合下的气隙磁密非对称性，建立了齿槽转矩的数学模型，并揭示了非对称气隙磁场中偶次谐波对齿槽转矩的具体影响。ZSOY等^[5]则致力于寻找最适合电动汽车驱动的电机方案，利用有限元方法对不同极数和槽数的双转子轴向磁通感应电机进行了全面分析，最终发现8极双转子轴向磁通电机在输出功率方面尤为突出。此外，黄磊等^[6]对不同极槽配合的内置式永磁同步电机在高速弱磁工况下的电磁性能进行了系统的比较分析。

在电机振动噪声的研究方面，左曙光等^[7]构筑了坚实的理论基础，系统剖析了不同极槽配合与绕组层数对电机最低阶径向力波的阶数和来源的影响。GUO等^[8]则进一步探讨了不同极槽配合对分数槽表贴式电机径向电磁力的影响，建立了磁场与径向电磁力之间的相位角和阶次关系，并发现对于槽数相近的电机，磁场谐波可通过齿调制产生与主谐波同阶且相位相反的分量，进而有效减小主径向力；而对于重叠绕组的电机，电枢谐波磁场相位的不同则可能导致径向力分量的叠加，从而增加径向力。针对大功率直驱永磁牵引电机在转速范围90～105 r/min内振动加剧的问题，吴楠等^[9]综合运用解析法、振动检测及有限元方法，精准定位问题根源，并通过调整极槽配合显著降低了电机的振动。此外，CHEN等^[10]提出了一种创新的电磁力-振动-声学分析模型，利用该模型深入分析了五相感应电动机的极槽方案对电磁噪声的影响，结果表明，特定极槽配合方案在降低电磁噪声方面具有显著效果。KIM等^[11]则对比分析了10极12槽与14极12槽内置式永磁同步电机在考虑齿调制效应下的电磁力和振动特性，结果显示，由于10极12槽电机具有较大的调制力，因此在振动方面相较于14极12槽电机处于不利地位。

综上所述，分析不同极槽配合对永磁同步电机电磁性能及电磁振动噪声的具体影响，不仅有助于人们深入理解电机内部电磁场的分布与变化规律，还能为电机设计的优化提供坚实的理论依据和实践指导。然而，目前多数文献的研究焦点往往局限于单一维度，或者侧重于不同极槽配合下的电机电磁性能分析，或者专注于振动噪声的探讨。鉴于车用驱动电机在实际应用中需兼顾卓越的电磁效率与低振动噪声的严苛要求，对上述两方面的综合性能进行全面而系统的分析显得尤为重要。

以8极48槽和8极36槽内置式永磁同步电机为研究对象，根据其设计参数，分别建立8极48槽和8极36槽永磁同步电机有限元模型，2个模型基本拓扑结构尺寸和永磁体用量保持一致。根据有限元模型比较分析不同极槽配合永磁同步电机的转矩波动、空载反电势及其谐波含量，以探究不同极槽配合对电机性能的影响。基于麦克斯韦张量法推导电磁力的解析模型，并通过解析模型和有限元模型分别分析不同极槽配合的电机电磁力的空间阶次和频率特征；建立电机多物理场耦合模型，分析对比不同极槽配合的电机结构模态和振动噪声特性。

1 永磁电机模型

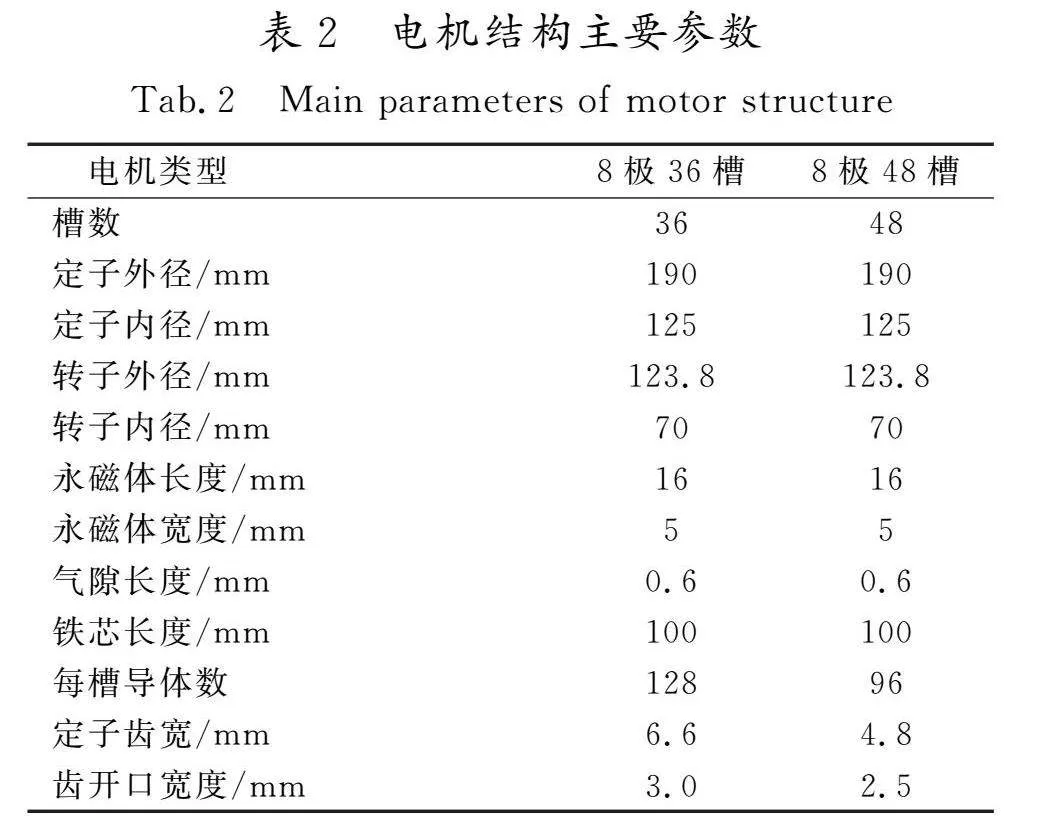
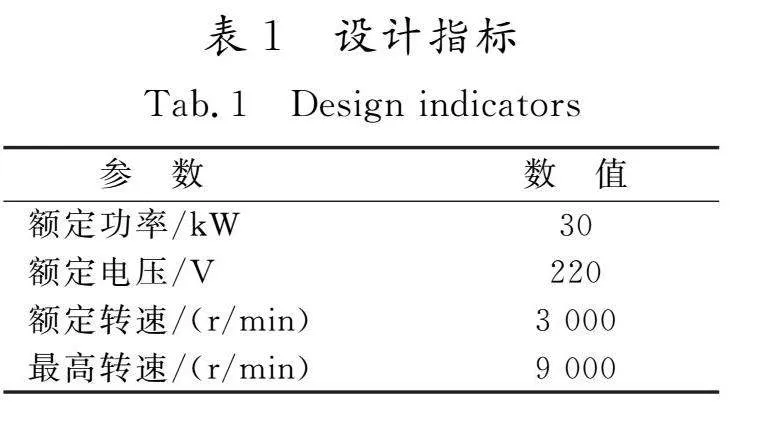
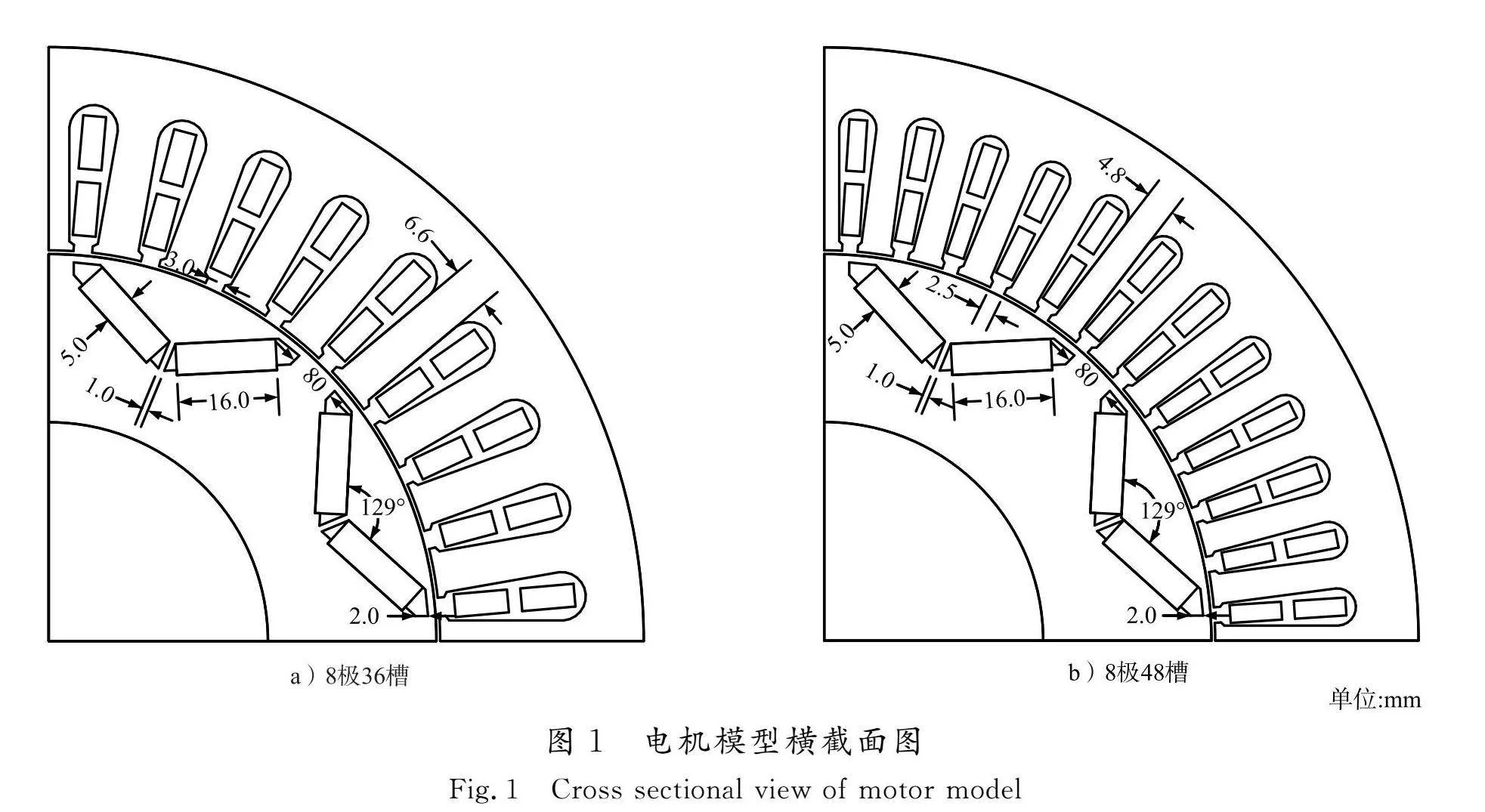
在电动汽车驱动领域，8极48槽内置式V型永磁同步电机凭借其卓越的效率特性和宽广的调速范围，已成为广泛采纳的解决方案。另一方面，8极36槽电机则凭借其分数槽设计的独特优势，在有效削弱齿槽转矩、增强电机运行平稳性方面展现出显著效果。鉴于此，本文选取这2种具有代表性的极槽配合电机作为深入研究的对象，旨在全面剖析其电磁性能及振动噪声特性。2台电机的设计指标如表1所示，其结构参数

如表2所示。

2台电机的主要尺寸相同，如定子内外径、转子内外径、气隙长度、永磁体用量等。为了确保电机公平性的对比，对2台电机的每槽导体数、定子齿宽、齿开口宽度进行了调整。2台内置式永磁同步电机模型的截面图如图1所示。

2 电磁性能分析

根据8极36槽和8极48槽2台电机模型，通过理论解析和有限元计算的方法分析了不同极槽配合对电机空载反电势、齿槽转矩、转矩波动的影响。

2.1 空载反电势

空载反电势的表达式为^[12]

Eφ t=2πNkNtftφt ， （1）

式中：N为电机线圈匝数；kNt为t次谐波绕组系数；ft为t次谐波电动势频率；φt为t次谐波每极磁通量；t为谐波次数，取奇数。

谐波绕组因数计算公式为

kNt=kytkqt=sin（ty1τπ2）sinqtα12qsintα12 ，（2）

式中：kyt为t次谐波的短距系数；kqt为t次谐波的分布系数；y1为绕组节距；τ为极距；q为每极每相槽数；α1为槽距电角度。

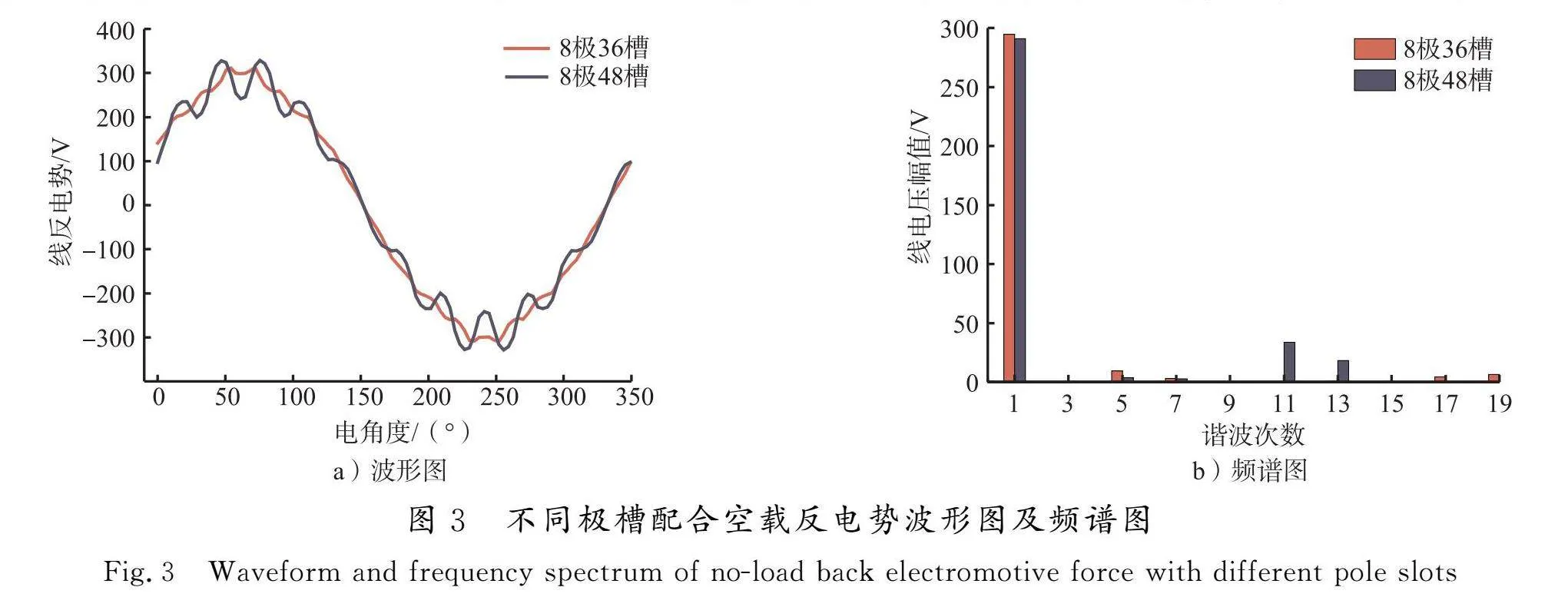
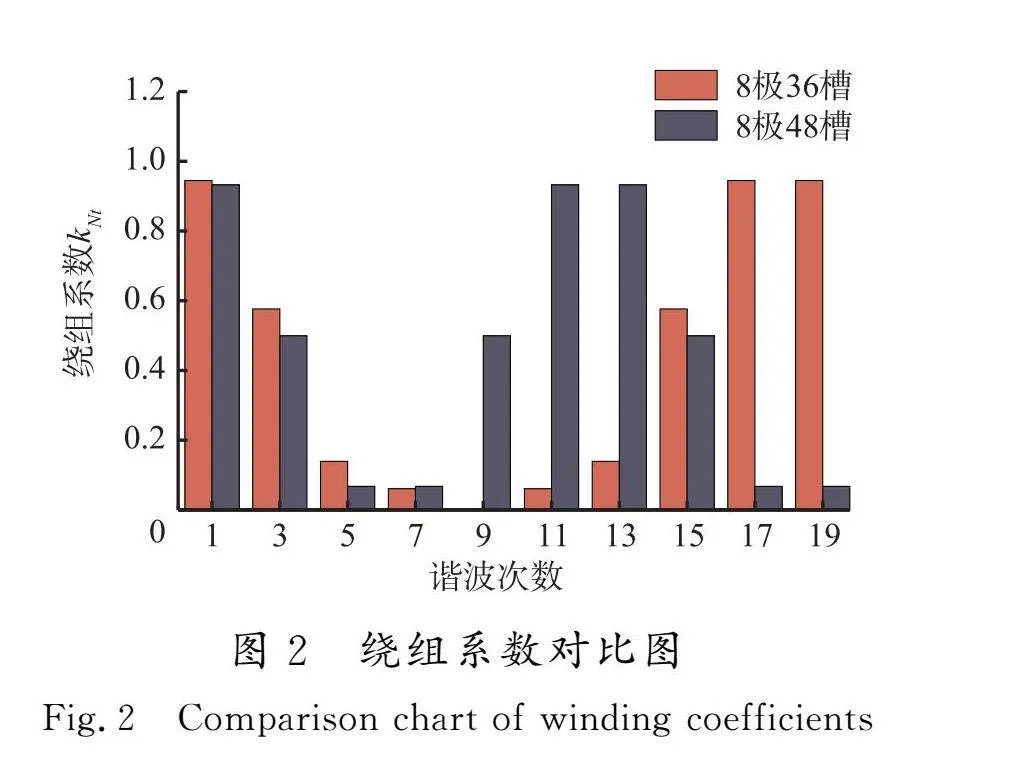
由空载反电势的表达式可知，影响空载反电势的因素包括线圈匝数、绕组因数、电动势频率、每极磁通量。对于本文2台不同极槽配合电机，转子结构和额定转速相同，因此其主要受线圈匝数和绕组因数的影响。在电机设计中，为了确保2台电机空载反电势有效值相近，对其匝数进行了修改，故此时空载反电势主要受绕组系数的影响，通过式（2）计算得到2台电机的不同谐波阶数绕组系数如图2所示。可以看出，36槽电机对于9、11、13次谐波削弱明显，而48槽电机对3、5、15、17、19次谐波削弱明显。

通过ANSYS-Maxwell分别建立8极36槽和8极48槽的二维有限元模型，设定其为空载工况，转速为额定转速，仿真得到电机的空载反电势波形，如图3所示，其有效值大小分别为208.6和207.5 V，再通过快速傅里叶变换（FFT）得到其频谱图，可以看出8极48槽电机的11、13次谐波明显高于8极36槽，与上述绕组系数分析结果相对应。为比较2台电机空载反电势的正弦度，引入谐波畸变率进行分析，其公式为

THD=（UH/U1）×100% ，（3）

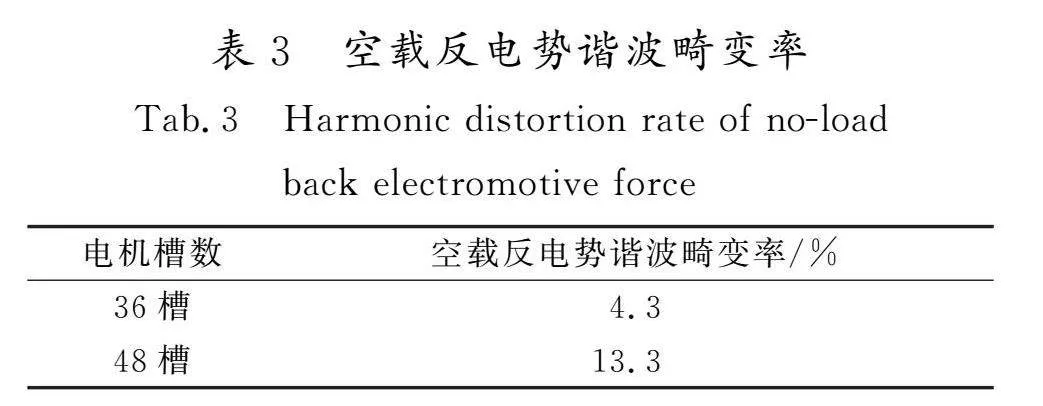
式中：THD为谐波畸变率；UH为其他谐波含量的均方根值；U1为基波的均方根值。2台电机空载反电势谐波畸变率如表3所示，可见36槽谐波畸变率比48槽谐波畸变率小，其正弦度更高，有利于电机的稳定运行。

2.2 齿槽转矩

在永磁同步电机中，永磁体与带槽的电枢铁心之间的相互作用会诱发齿槽转矩，这是一种随定转子相对位置变化而正负交替的转矩波动。这种波动不仅叠加在电机的电磁转矩上，降低控制精度，还可能引发电磁振动和噪声问题。为探究槽极数配合对齿槽转矩的影响，基于能量法对齿槽转矩进行推导，数学表达式^[13]见式（4）。

Tcog（α）=μ0πQsLa4

（R22-R21）∑∞n=1uGuFwsin（uQsα） ，（4）

w=uQs2p ，（5）

式中：Qs为定子槽数；p为极对数；La为电枢铁心的轴向长度；R1和R2分别是转子铁心的外半径和定子铁心的内半径；Gu为电机气隙长度分布傅里叶展开后的各阶次幅值；Fw为电机气隙磁动势分布傅里叶展开后的各阶次幅值；u为确保w为整数的整数。

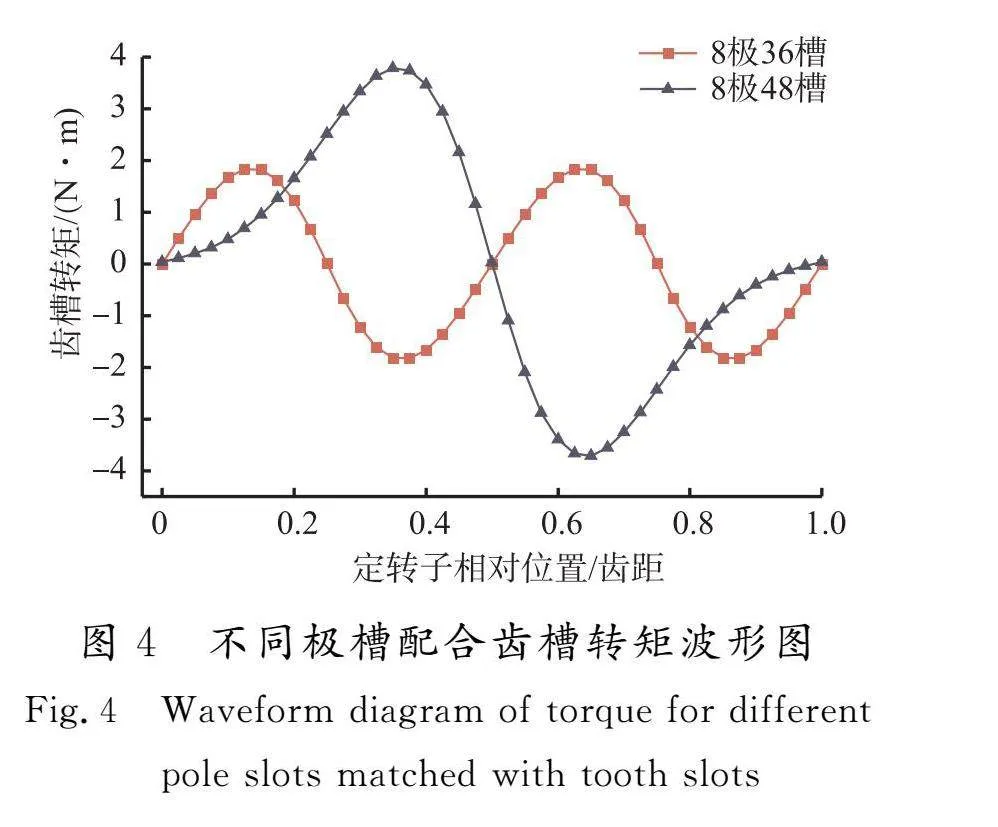
图4为不同极槽配合齿槽转矩波形图。可以看出，在定转子相对位置变化一个齿距内，齿槽转矩具有周期性，其周期性取决于极槽配合，周期数为u的最小值，公式为

Np=2PGCD（Qs，2P） ，（6）

式中：Np为周期数；GCD（Qs，2P）为电机槽数和极数的最大公约数。以本文2台电机为例，8极48槽电机的周期数为 而8极36槽电机的周期数为 与图4中的波形图吻合。

进一步分析图4可以发现，齿槽转矩的周期数与齿槽转矩幅值之间存在显著关系：周期数越多，齿槽转矩的幅值越小，齿槽转矩幅值主要取决于Fw，而Fw随着w的增加而逐渐衰减。由于周期数决定了w的最小值，因此周期数的增加会导致w的最小值增大，进而使得Fw减小，最终降低齿槽转矩的幅值。综上所述，分数槽电机因具有更大的周期数，其相较于整数槽电机对齿槽转矩的削弱更具优势。

2.3 转矩波动

在电机体积相等、转速为3 000" r/min的条件下，通入有效值为75 A的相电流，对2台电机额定工况进行有限元分析，得到的波形见图5。结合图中数据，可计算出2台电机的转矩波动^[14]为

Tn=Tmax-TminTavg×100% ，（7）

式中：Tn为转矩波动；Tmax为转矩脉动最大值；Tmin为转矩脉动最小值；Tavg为转矩脉动平均值。

由图5和式（7）可知，36槽电机的转矩波动为10.72%，平均转矩为96.19 N·m，48槽电机的转矩波动为16.03%，平均转矩为96.60 N·m。通过对比发现，分数槽电机的转矩输出相较于整数槽电机更加稳定，但在相同电流输入时，分数槽的平均转矩要低于整数槽的，这是因为各极下绕组分布不对称从而使电机的有限转矩分量部分被抵消。

3 气隙电磁力分析

3.1 理论分析

对于电机而言，气隙中的磁场可以看作一个旋转力波，其作用在定子齿上，引起定子产生变形和周期性振动，因此，对电机振动噪声的分析，首先要对电机气隙处的电磁力波进行分析。

根据麦克斯韦张量法可知，径向电磁力可以用径向和切向气隙磁通密度表示：

fr=B2r-B2t2μ0≈B2r2μ0 ，（8）

式中：Br和Bt分别是电机气隙磁通密度的径向和切向分量；μ0为真空磁导率。一般情况下，径向电磁力可以由径向气隙磁通密度表示，因为切向气隙磁通密度相比径向气隙磁通密度非常小。

径向磁通密度可以由永磁磁场、电枢磁场和相对磁导表示^[15-16]：

Br=（BPM+Barm）λa ，（9）

BPM=∑nBmncos（npθ-2πnf1t+βn） ，（10）

Barm=∑vBavcos（vpθ-2πsvf1t+βv） ，（11）

λa=λ0+∑μλaμcos（μQsθ） ，（12）

式中：BPM和Barm分别是永磁磁场和电枢反应磁场产生的径向磁通密度；

m为相数；λa为考虑开槽效应的等效气隙磁导；n为永磁场空间谐波阶数，n=2i+1（i=0， …）；p为电机极对数；θ为转子机械角度；f1为电流基频；t为时间；β为相位；v为电枢反应磁场谐波次数；sv的值取决于次电枢反应磁场的旋转方向（当v次电枢反应磁场向前旋转时，sv=1；反之，sv=-1）；Qs为定子槽数；μ为齿谐波阶数。

电枢反应磁场的空间谐波次数根据极槽配合决定，其可表示为

q=Qs2mp=bc， v=6kc+1 ，（13）

式中：b和c互为质数；k=0， …，对于本文2台电机，48槽电机v=6k± 36槽电机v=3k±1。

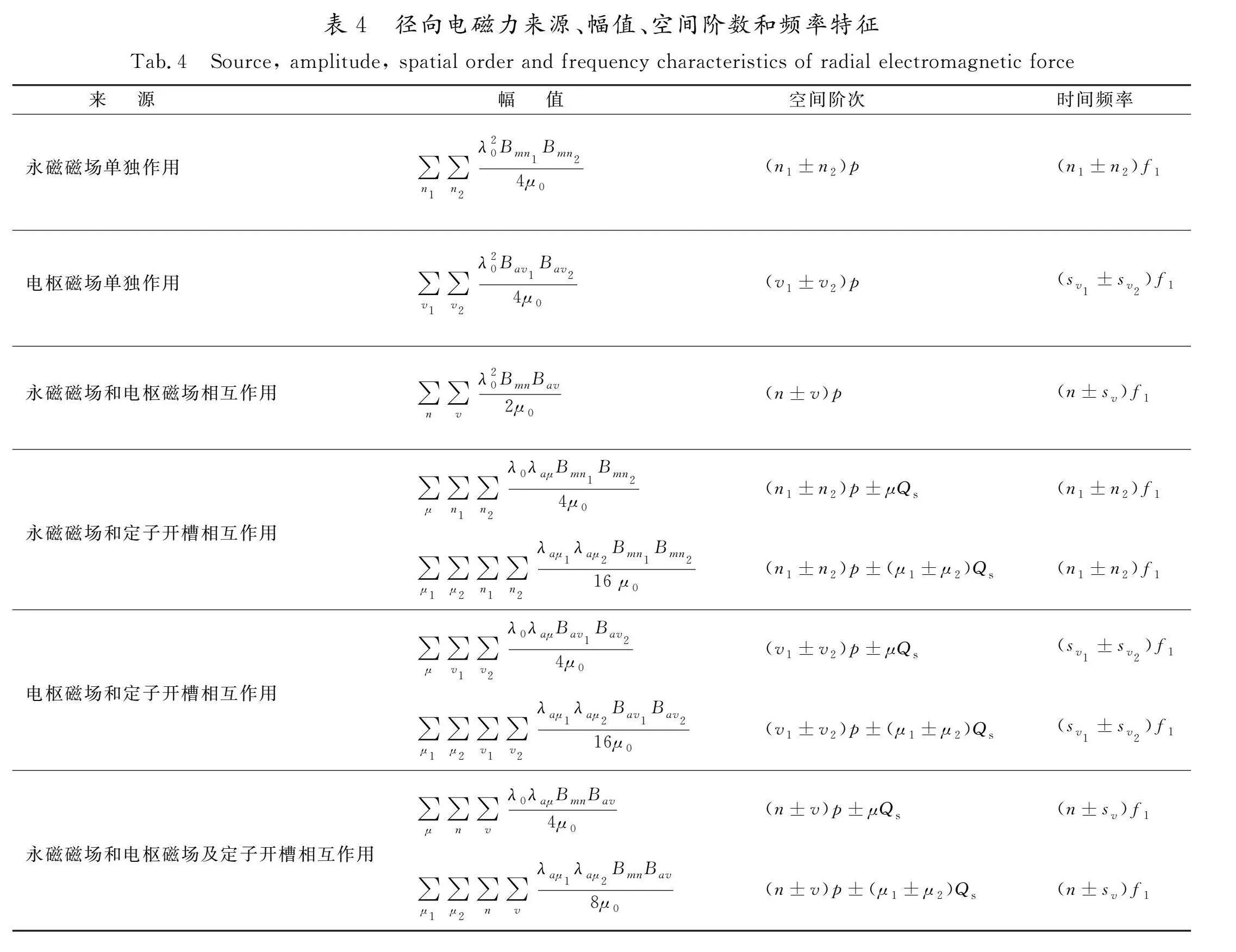
将式（9）—（12）代入式（8），可得定子铁心所受到的径向电磁力的详细表达式。表达式中总共有9项，再根据三角函数积化和差公式进行简化，可以获取径向电磁力的来源、幅值、空间阶数和频率特征，如表4所示。

为了突出对比不同极槽配合电机的电磁力阶次，结合表4中的空间阶次和时间频率特征，对本文2台不同极槽配合电机进行分析，总结归纳出其主要电磁力波阶次和时间频率如表5、表6所示（表中数据均以a/b形式，其中a表示电磁力波空间阶次，b代表电磁力波频率相对于基频的倍数）。表中只列出了幅值较高的永磁磁场和电枢磁场与气隙磁导恒定分量和低次谐波分量相互作用的结果。带括号项表示永磁磁场和电枢磁场与气隙磁导低次谐波分量相互作用的结果，负号表示与基波磁场的旋转方向相反；不带括号项表示永磁磁场和电枢磁场与气隙磁导恒定分量相互作用的结果，负号含义同上。

3.2 有限元分析

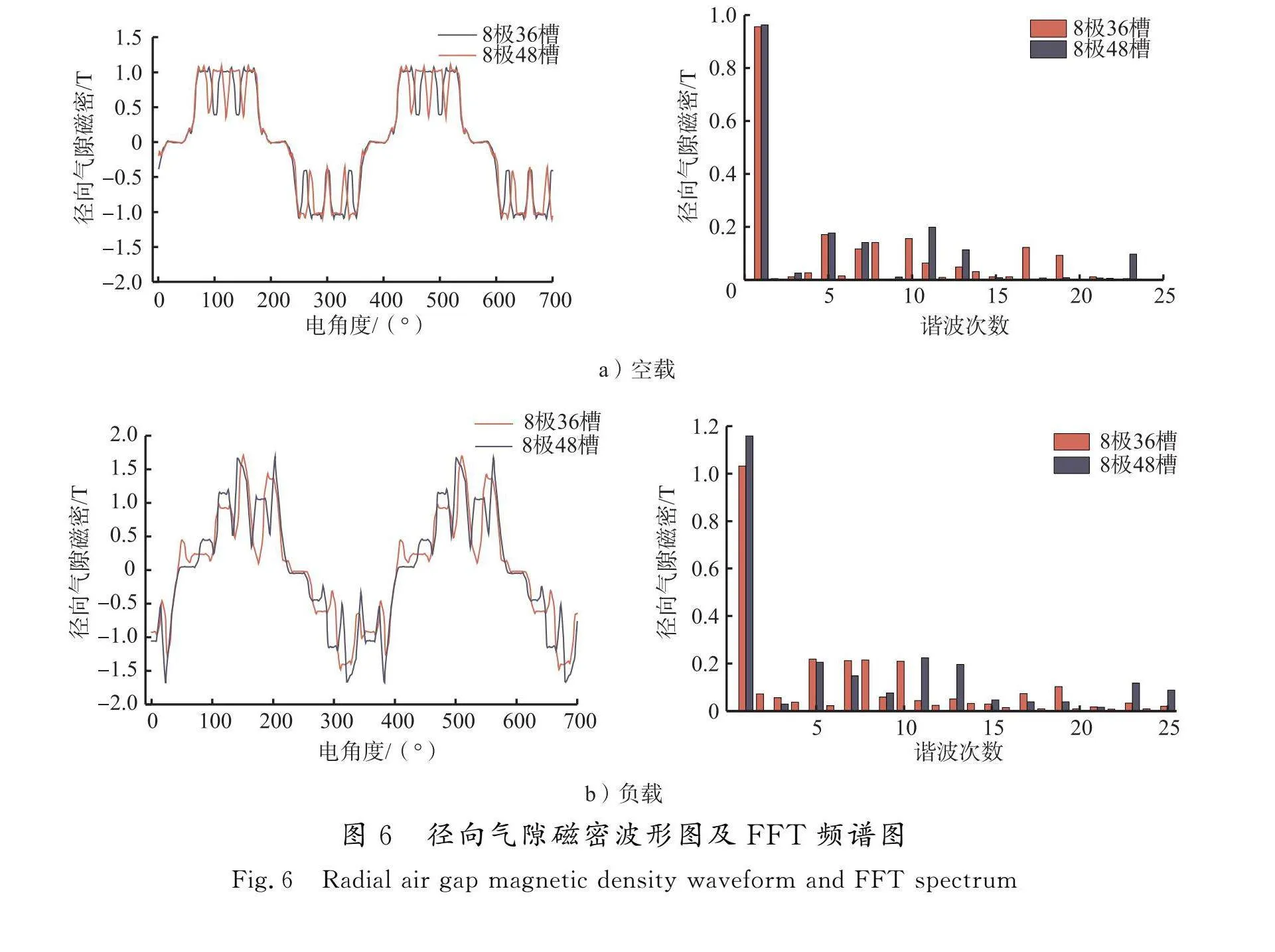
根据式（8）可知，电机径向电磁力的大小主要由径向气隙磁密确定。为了获得更精确的结果，对本文2台电机模型的空载工况和负载工况进行有限元分析。2台电机的负载工况均以额定功率和额定转速进行有限元计算，得出径向气隙磁密波形图和FFT频谱图，如图6所示。对比电机空载工况和负载工况可以发现，负载工况由于通入电流谐波，谐波含量高且各阶次谐波幅值有所增加，气隙磁密波形正弦度降低。对比2台电机可以发现，径向气隙磁密波形幅值相差不大。通过频谱图对比可以看出，48槽电机基波幅值大，低阶谐波幅值低，谐波含量少。因此，相对36槽电机，48槽电机径向气隙磁密波形具有更高的正弦度。

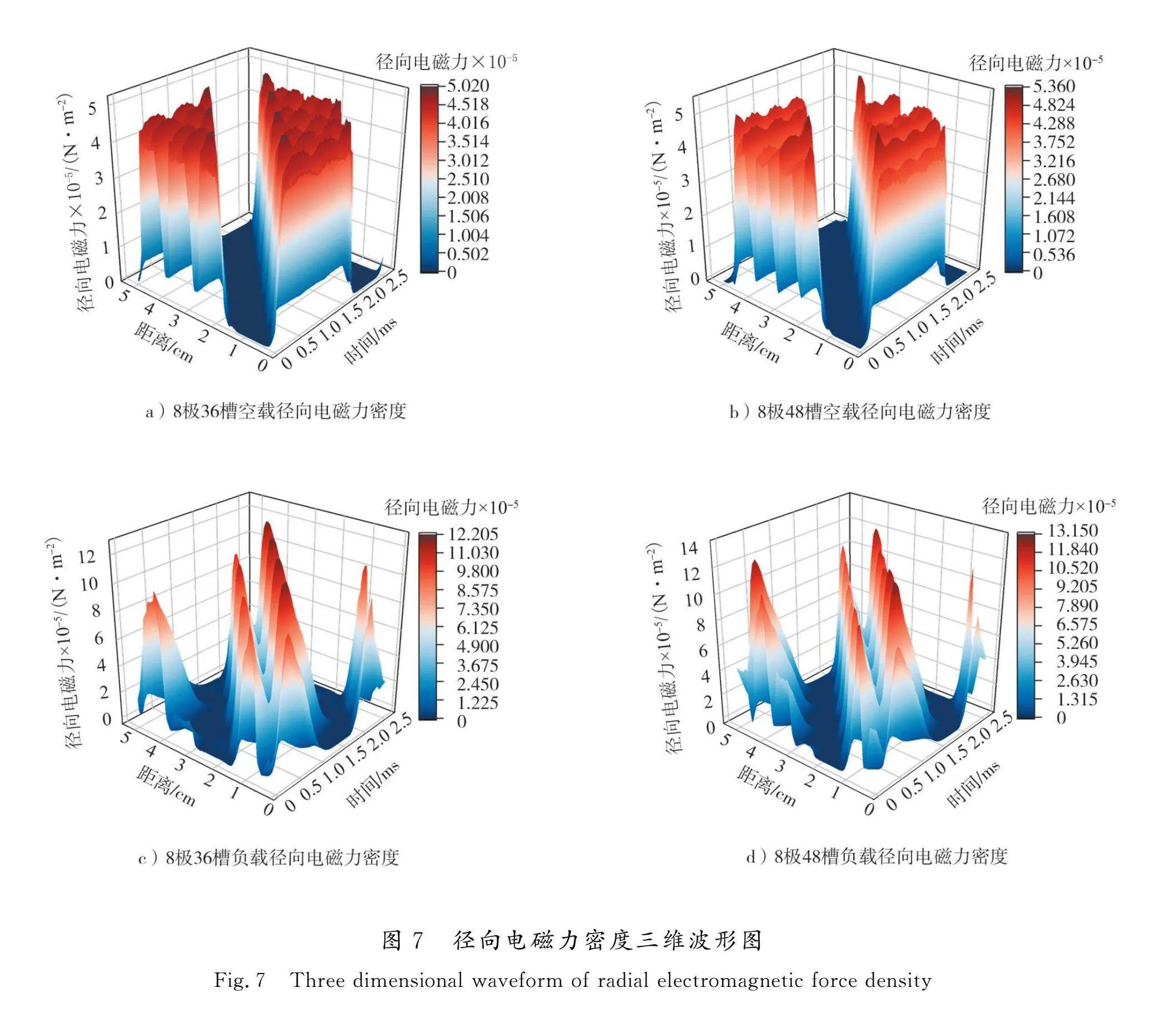
径向电磁力波具有时间和空间2个特性，为了更好地分析径向电磁力，通过有限元分析得到2台电机在空载和负载工况下的径向电磁力波的三维波形图如图7所示。通过图7可以看出，48槽电机在2种工况下的径向电磁力波幅值均比36槽电机高，负载工况更为明显，这是因为48槽电机的径向气隙磁密基波幅值比36槽电机的径向气隙磁密基波幅值高，负载工况两台电机径向气隙磁密基波幅值相差更大。

为了深入探究径向电磁力波的阶次特征，采用二维傅里叶分解对电机产生的径向电磁力波进行分析，主要聚焦于2台电机在各自2种不同工况下的表现，所生成的谐波含量图如图8所示。

基于定子形状为圆柱模型的传统位移方程，力波阶次和电机振动位移的关系^[17-18]可以表示为

Y=12R2R3yokeEl3yoke

（r2-1）2fr ，（14）

式中：Y是位移；R2是定子内半径；Ryoke是平均轭半径；r是振动阶次；E是等效环模型的弹性模量；l³yoke为定子轭宽度。

可以看出，电机振动位移与振动阶次的四次方成反比，所以空间阶数越高对电磁振动的贡献越小。分析图8可知，径向电磁力波主要电磁力阶次与表5、表6所示一致，空间阶次均为极对数的偶数倍，时间分量均为电流基频的偶数倍，其中幅值最高的谐波为（0，0f），但其为时间和空间均不变的静态力，对振动噪声影响很小。值得关注的是（0，6f）、（0，12f）等随时间变化的空间零阶次电磁力，对于本文2台电机，36槽电机主要零阶电磁力为（0，6f），而48槽电机主要零阶电磁力为（0，12f）且幅值较高，可能会对电机振动噪声产生影响。对于2台电机的空间非零阶次电磁力，从图8中可以看出，36槽电机的最低空间非零阶次电磁力阶次为（- 2f）、（- 8f）、（ 4f）、（ 10f），其中（- 8f）幅值偏高，48槽电机的最低空间非零阶次电磁力阶次

为（8，2f），因此36槽电机容易发生比较大的振动，在设计过程中需要提高定子的固有频率以避免与空间阶次为4的电磁力发生共振。对比2台电机的空载和负载工况可以发现，其随时间变化的空间零阶次电磁力的产生以及36槽电机的最低空间非零阶次电磁力比48槽电机低主要是因为负载工况下电流谐波的注入。

4 电机模态分析

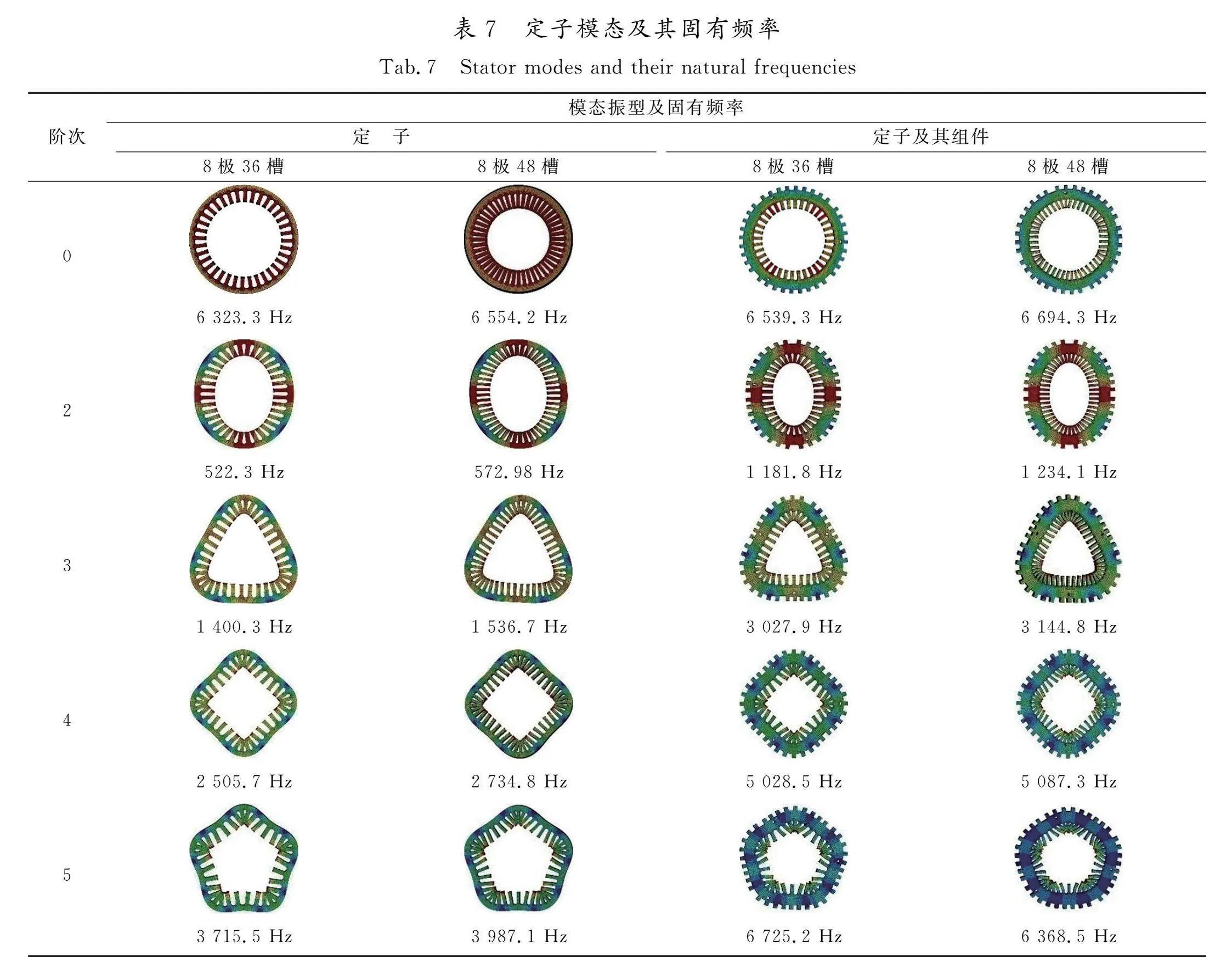
模态分析能够准确识别电机的各阶固有频率以及模态振型，固有频率是电机结构在自由振动时的特定频率，当外部激励频率接近或等于固有频率时，电机可能会发生共振，导致振动加剧^[19-21]。而通过分析电机的模态振型，可以了解电机在不同频率下的振动形态，有助于确定电机振动的主要贡献模态，为后续的振动控制和噪声抑制提供依据。

本文利用有限元法对电机定子及其组件进行自由模态求解。由于2款电机无转子斜极，且电机轴向电磁力分布相近，忽略模型轴向模态，求解得到的定子及其组件的模态振型及固有频率如表7所示。由表7可以看出，2款电机定子及其组件模态频率相近，48槽电机定子及其转子模态频率略高于36槽电机，而且添加机壳有利于提高固有频率，减少多转速运行下共振的可能。

5 电机振动噪声分析

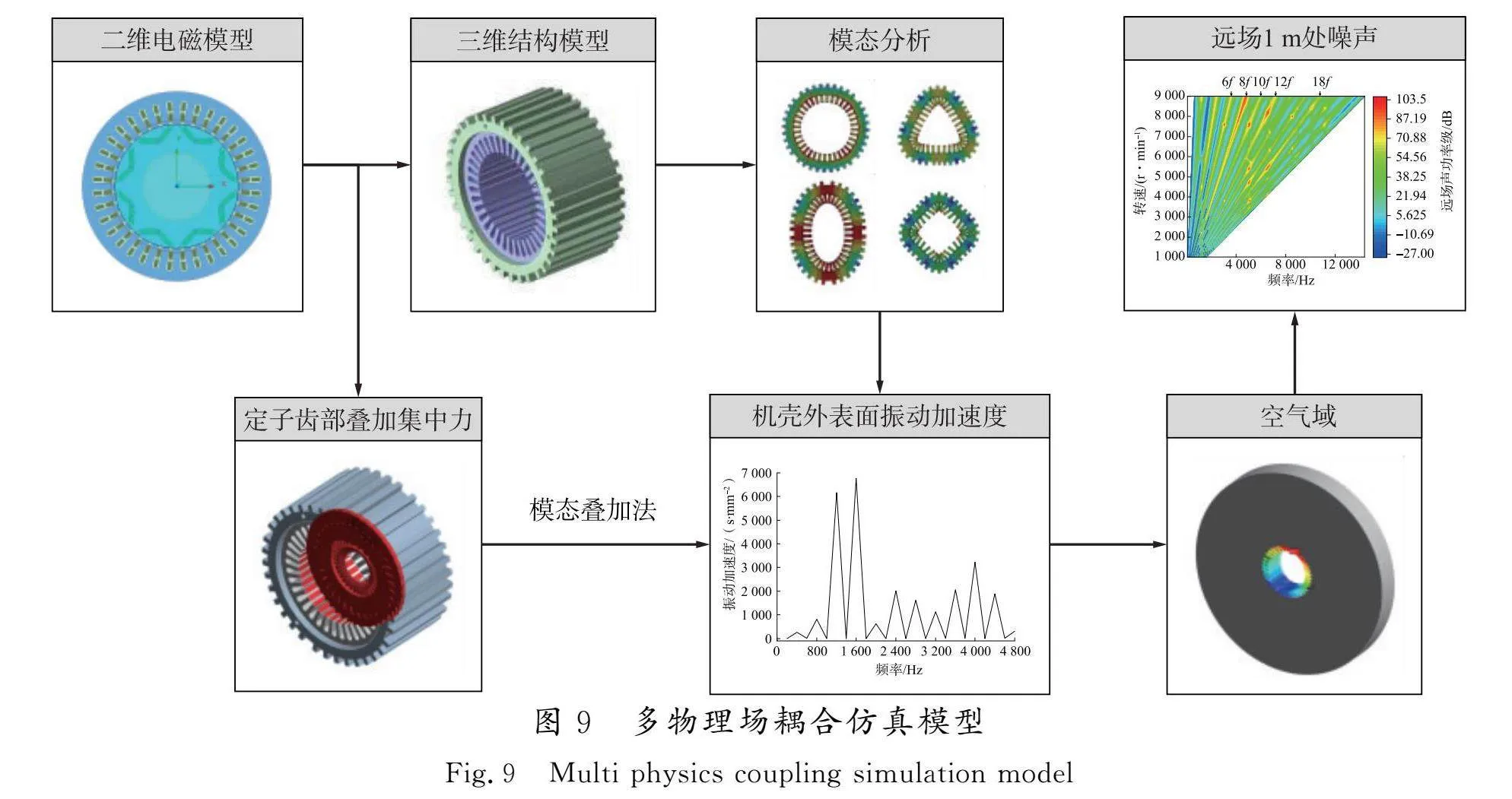
为了对比分析极槽配合对电机振动噪声的影响，建立多物理场耦合仿真模型，如图9所示。通过二维电磁模型计算定子齿部所受电磁力，电磁力以集中力的形式体现；将求解所得齿部电磁

力导入三维结构模型，结合三维结构模型模态分析结果，采用模态叠加法对机壳表面振动加速度进行求解；建立远场1 m处空气域，将机壳表面加速度添加到空气域内表面，继而求解电机远场1 m处噪声。

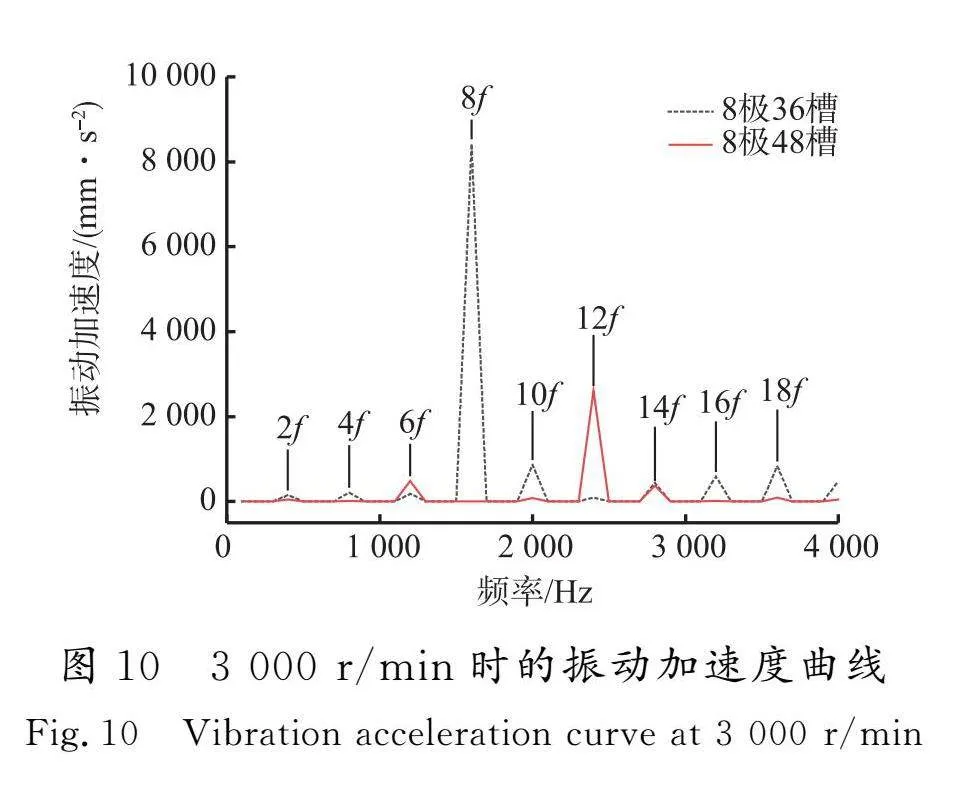
通过上述多物理场耦合仿真模型对2台电机额定工况3 000 r/min 转速下的振动加速度进行仿真，得到机壳表面振动加速度如图10所示。由图10可以看出，振动加速度大的频率与激振力波的频率相同，均为电机电流基频的偶数倍。另外，8极36槽电机振动加速度峰值在8f处，结合上述对电机径向电磁力的分析，其主要是由径向电磁力（- 8f）导致的。由表5可知，径向电磁力（- 8f）主要是由永磁磁场7p、9p次谐波与电枢磁场1p次谐波以及1阶齿谐波相互作用生成。而8极48槽电机振动加速度峰值在12f处，其主要是由径向电磁力（0，12f）导致的，说明电磁振动主要与低阶电磁力谐波和零阶电磁力谐波有关。由表6可知，径向电磁力（0，12f）主要是由永磁磁场11p、13p次谐波与电枢磁场1p次谐波以及1阶齿谐波相互作用生成。在后续优化时应着重对这些谐波进行抑制。

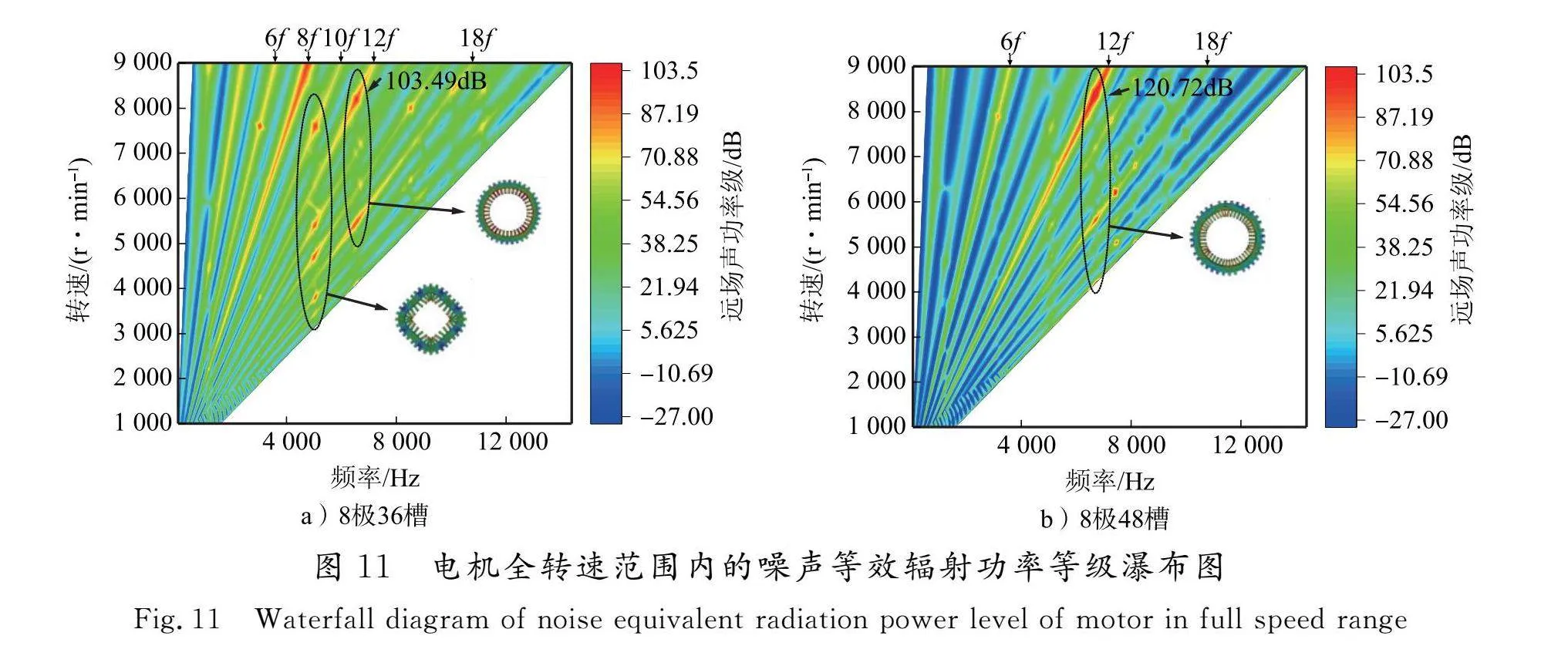
为了更好地分析电机在全转速范围内的噪声响应，基于上述所建多物理场耦合模型，对2台电机的噪声频谱特性进行分析。本文电机转速为1 000～9 000 r/min，为获得精确结果，以100" r/min为转速增加步长，得到远场1 m处噪声等效辐射功率等级瀑布图如图11所示。可以看出，对于8极36槽电机，当其运行频率接近8f时，其产生的电磁噪声幅值大，而对于8极48槽电机，其运行频率接近12f时，产生的电磁噪声幅值大，与上述分析电磁振动结果相似，均由低阶电磁力与零阶电磁力产生。

电磁力激励下的定子共振需要同时满足电磁力空间阶数等于定子的模态阶数以及此阶数的电磁力包含的频率靠近对应阶数的定子模态频率^[22-23]。由图11可以看出，8极36槽电机在5 000 Hz和6 500 Hz附近会出现噪声幅值增大，结合表7和图8可以发现，2个频率带分别与4阶振型和0阶振型的固有频率接近，且噪声为空间4阶电磁力谐波与零阶电磁力谐波导致，因此即使激振力波幅值不是很高也会发生共振，从而导致噪声幅值大幅度增加，而对于8极48槽电机，其零阶振型固有频率为6 694.3 Hz，因此在6 700 Hz附近出现噪声幅值大幅度增加。对比2款电机噪声峰值，8极36槽电机噪声峰值为103.49 dB，8极48槽电机噪声峰值为120.72 dB，其出现位置如图11所示，均由（0，12f）电磁力导致，因8极48槽电机该阶次电磁力幅值大，故其噪声幅值大。虽然8极48槽电机在全转速运行范围内噪声峰值比8极36槽电机噪声峰值高，但其主要受零阶电磁力波的影响，无其他低阶电磁力波，除了共振区域，幅值均低于8极36槽电机，因此，在宽调速范围8极48槽电机相比于8极36槽电机更有利于噪声的抑制。

通过上述分析，车用永磁同步电机的振动噪声主要源自低阶径向电磁力的激励以及系统共振的产生，其中共振问题可通过提升定子及其组件的固有频率进行规避。低阶电磁力主要是由永磁磁场、电枢反应磁场以及定子开槽相互作用产生，对于内置式永磁同步电机，其永磁磁场主要与转子结构有关，可通过改变极弧系数、隔磁桥宽度、改变转子拓扑结构等方式对其产生的谐波进行抑制；电枢磁场则主要与绕组的布局和电枢电流产生的谐波有关，可通过改变绕组层数以及谐波注入的方式对谐波进行抑制；齿谐波主要由定子开槽产生，可通过调整定子槽开口宽度的方式对谐波进行抑制。

6 结 语

本文以8极48槽和8极36槽内置式永磁同步电机为研究对象，对电机的空载反电势、齿槽转矩、转矩脉动、径向电磁力密度、定子模态以及电磁振动噪声性能进行分析比较，主要结论如下。

1）8极36槽电机由于其绕组系数对空载反电势低阶谐波的抑制更为明显，以及齿槽转矩周期数多，在电机的稳定运行上，要优于8极48槽电机，但由于其各极下绕组分布不对称，会使电机的有限转矩分量部分被抵消。

2）径向电磁力是电机产生电磁振动的主要原因，极槽配合的不同会对电机的谐波阶次以及其幅值产生影响。在空载工况下，8极36槽电机和8极48槽电机的最小电磁力谐波非零空间阶次均为8阶，而在负载工况下，8极36槽电机出现了更低的空间4阶电磁力，说明36槽电机的低空间阶次电磁力谐波主要是由电枢反应磁场导致的。

3）8极36槽电机振动峰值集中在8f处，由低阶径向电磁力谐波（- 8f）导致，其主要是由永磁磁场7p、9p次谐波与电枢磁场1p次谐波以及1阶齿谐波相互作用生成，而8极48槽电机振动峰值集中在12f处，由零阶径向电磁力（0，12f）导致，其主要是由永磁磁场11p、13p次谐波与电枢磁场1p次谐波以及1阶齿谐波相互作用生成，说明电磁振动主要与低阶电磁力和零阶电磁力有关，在后续优化时应着重对这些谐波进行抑制。

4）电机在宽转速范围运行时，对比两款电机噪声峰值，8极36槽电机噪声峰值为103.49 dB，8极48槽电机噪声峰值为120.72 dB，均由（0，12f）电磁力导致，因8极48槽电机该阶次电磁力幅值大，故其噪声幅值大。虽然8极48槽电机在全转速运行范围内噪声峰值比8极36槽电机噪声峰值高，但其主要受零阶电磁力波的影响，无其他低阶电磁力波，除了共振区域，幅值均低于8极36槽电机，因此，在宽调速范围8极48槽电机相比于8极36槽电机更有利于噪声的抑制。

综上所述，8极36槽与8极48槽内置式永磁同步电机各有优势，8极36槽电机在稳定运行和转矩特性上表现更佳，而8极48槽电机在宽调速范围内有利于噪声抑制。分析得出了8极36槽和8极48槽电机产生振动噪声的主要径向电磁力激励源，对后续采用调整电机极弧系数、隔磁桥宽度、绕组层数和改变转子拓扑等结构优化方式抑制特定阶次径向电磁力谐波，从而显著抑制电机振动噪声，提高电动汽车舒适性具有指导作用。

本文只对比分析了不同极槽配合对分布式绕组电机电磁性能以及振动噪声的影响，后续还需进一步分析不同极槽配合对近极槽配合集中式绕组电机电磁性能以及振动噪声的影响。

参考文献/References：

[1] 唐任远.现代永磁电机[M].北京：机械工业出版社，2016.

[2] 马伟明，王东，程思为，等.高性能电机系统的共性基础科学问题与技术发展前沿[J].中国电机工程学报，2016，36（8）：2025-2035.

MA Weiming，WANG Dong，CHENG Siwei，et al.Common basic scientific problems and development of leading-edge technology of high performance motor system[J].Proceedings of the CSEE，2016，36（8）：2025-2035.

[3] KIMS Y.A study on motor characteristics based on pole-slot combinations[J].AIP Advances，2024.DOI： 10.1063/9.0000647.

[4] 李烽，王凯，高培伟，等.不同极槽配合交替极永磁电机齿槽转矩和转矩脉动的研究[J].中国电机工程学报，202 42（17）：6491-6498.

LI Feng，WANG Kai，GAO Peiwei，et al.Investigation of cogging torque and torque ripple in consequent pole permanent magnet machine with different slot/pole number combinations[J].Proceedings of the CSEE，202 42（17）：6491-6498.

[5] ZSOY M，KAPLAN O，AKAR M.The effect of stator slot number and pole number on motor performance in double-sided axial flux induction motors for electric vehicles[J].Electrical Engineering，202 104（6）：4289-4304.

[6] 黄磊，彭兵.不同极槽配合电动汽车永磁同步电机弱磁性能及抗饱和能力研究[J].微电机，2020，53（11）：61-64.

HUANG Lei，PENG Bing.Research on flux weakening performance and anti-saturation capability of IPM machines having different pole/slot number combinations[J].Micromotors，2020，53（11）：61-64.

[7] 左曙光，林福，孙庆，等.极槽配合和绕组层数对永磁同步电机振动的影响分析[J].振动与冲击，201 33（13）：130-134.

ZUO Shuguang，LIN Fu，SUN Qing，et al. Analysis of vibration in permanent magnet synchronous motor with different slot-pole combinations and winding layers[J].Journal of Vibration and Shock，201 33（13）：130-134.

[8] GUO Y D，WANG K，SUN H Y.Influence of magnet field harmonics on radial force of fractional-slot PM machines considering slot/pole combinations[J].IEEE Transactions on Magnetics，202 59（11）：1-6.

[9] 吴楠，迟连强，李嘉宾，等.直驱永磁牵引电机振动原因分析[J].城市轨道交通研究，202 26（12）：143-146.

WU Nan，CHI Lianqiang，LI Jiabin，et al.Cause analysis of direct-drive permanent magnet traction motor vibration[J].Urban Mass Transit，202 26（12）：143-146.

[10]CHEN Qixu，CHEN Zhizhong，LI Guoli，et al.Comparative analysis of vibration and noise of axial flux motor with different pole and slot combinations[J].Chinese Journal of Electrical Engineering，202 9（4）：144-156.

[11]KIM J H，PARK S H，RYU J Y，et al.Comparative study of vibration on 10-pole 12-slot and 14-pole 12-slot PMSM considering tooth modulation effect[J].IEEE Transactions on Industrial Electronics，202 70（4）：4007-4017.

[12]辜承林，陈乔夫，熊永前.电机学[M].武汉：华中科技大学出版社，2010.

[13]王秀和，杨玉波，朱常青，等.永磁同步电机：基础理论，共性问题与电磁设计[M].北京：机械工业出版社，2022.

[14]胡耀华.电动汽车用内置式永磁同步电机的研究[D].南京：南京航空航天大学，2017.

HU Yaohua.Research on Interior Permanent Magnet Synchronous Machines for EV Applications[D].Nanjing：Nanjing University of Aeronautics and Astronautics，2017.

[15]高辉，尹红彬，王永超，等.不同槽极数配合的永磁电机噪声特性分析[J].微电机，2019，52（3）：1-4.

GAO Hui，YIN Hongbin，WANG Yongchao，et al.Noise analysis of permanent magnet motors with different slot-pole combinations[J].Micromotors，2019，52（3）：1-4.

[16]陈鹏飞，尹红彬，张学义，等.内嵌式永磁电机电磁振动噪声多物理场仿真与优化[J].汽车技术，2020（12）：25-29.

CHEN Pengfei，YIN Hongbin，ZHANG Xueyi，et al.Multi-physics field simulation and optimization of electromagnetic vibration amp; noise of interior permanent magnet synchronous motor[J].Automobile Technology，2020（12）：25-29.

[17]马霖，陈学军.定子槽结构的永磁同步电机振动噪声优化[J].福州大学学报（自然科学版），202 52（2）：198-206.

MA Lin，CHEN Xuejun.Vibration and noise optimization of permanent magnet synchronous motor based on stator slot structure[J].Journal of Fuzhou University（Natural Science Edition），202 52（2）：198-206.

[18]FANG Haiyang，LI Dawei，QU Ronghai，et al.Modulation effect of slotted structure on vibration response in electrical machines[J].IEEE Transactions on Industrial Electronics，2019，66（4）：2998-3007.

[19]WANG Shanming，HONG Jianfeng，SUN Yuguang，et al.Analysis of zeroth-mode slot frequency vibration of integer slot permanent-magnet synchronous motors[J].IEEE Transactions on Industrial Electronics，2020，67（4）：2954-2964.

[20]陈永校.电机噪声的分析和控制[M].杭州：浙江大学出版社，1987.

[21]LEE Y G，BANG T K，LEE J I，et al.Characteristic analysis and experimental verification of electromagnetic and vibration/noise aspects of fractional-slot concentrated winding IPMSMs of e-Bike[J].Energies，2022.DOI： 10.3390/en15010238.

[22]左曙光，吴旭东.车用同步电机噪声与振动[M].北京：机械工业出版社，2021.

[23]宋腾飞.电动汽车永磁同步电机电磁振动噪声特性与抑制研究[D].北京：北京交通大学，2022.

SONG Tengfei.Electromagnetic Vibration and Noise Characteristics and Its Suppression of Permanent Magnet Synchronous Motor Used for Electric Vehicles[D].Beijing：Beijing Jiaotong University，2022.