求解逆拟变分不等式的时滞神经网络

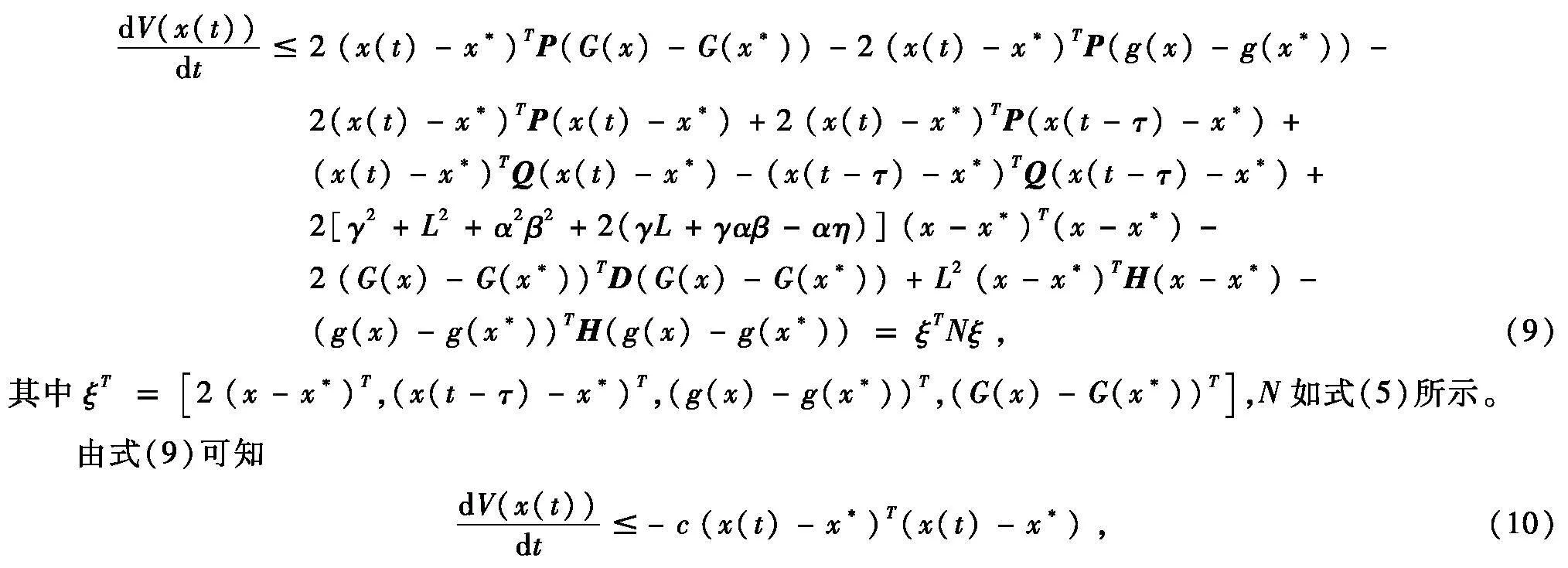
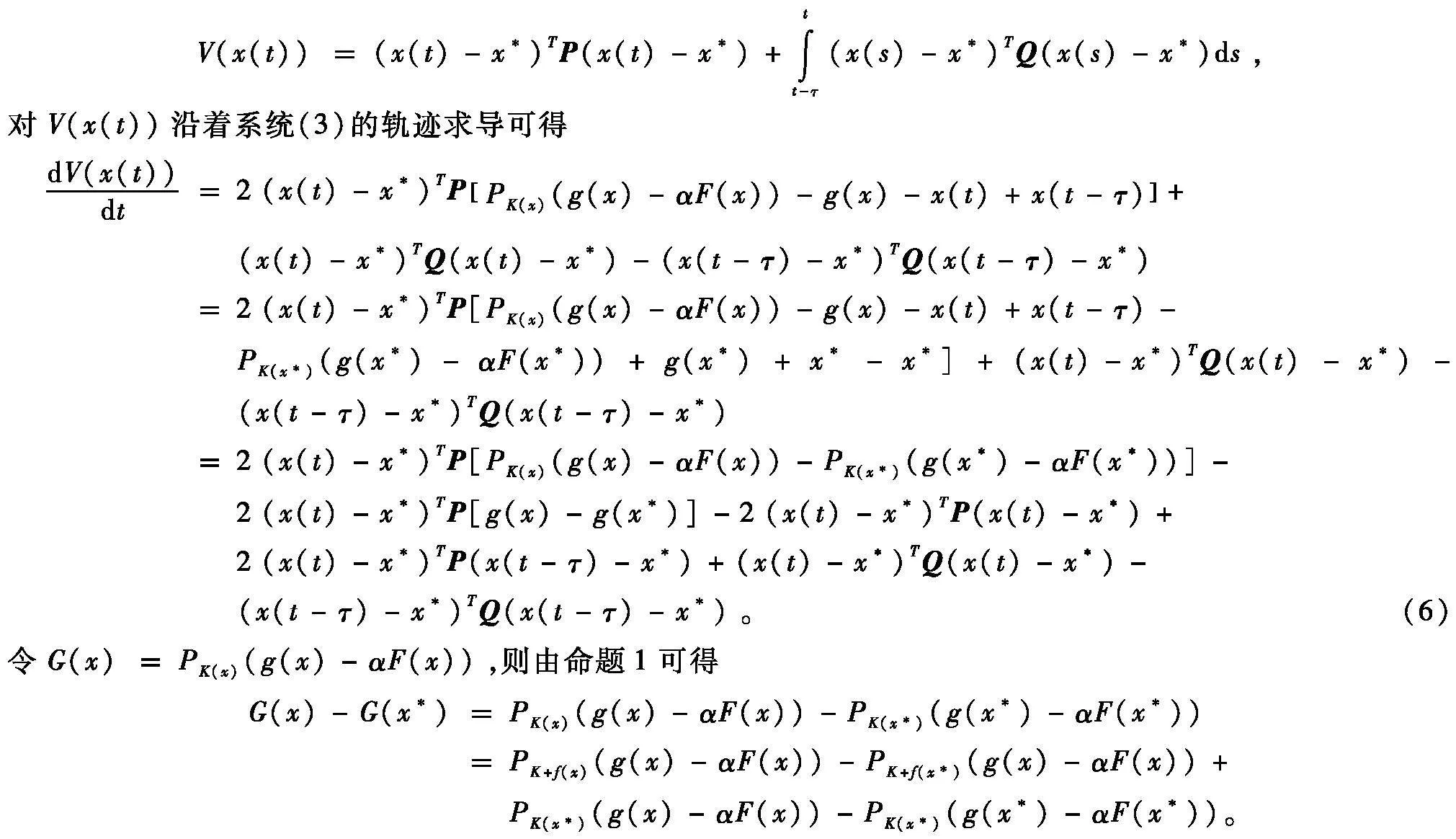
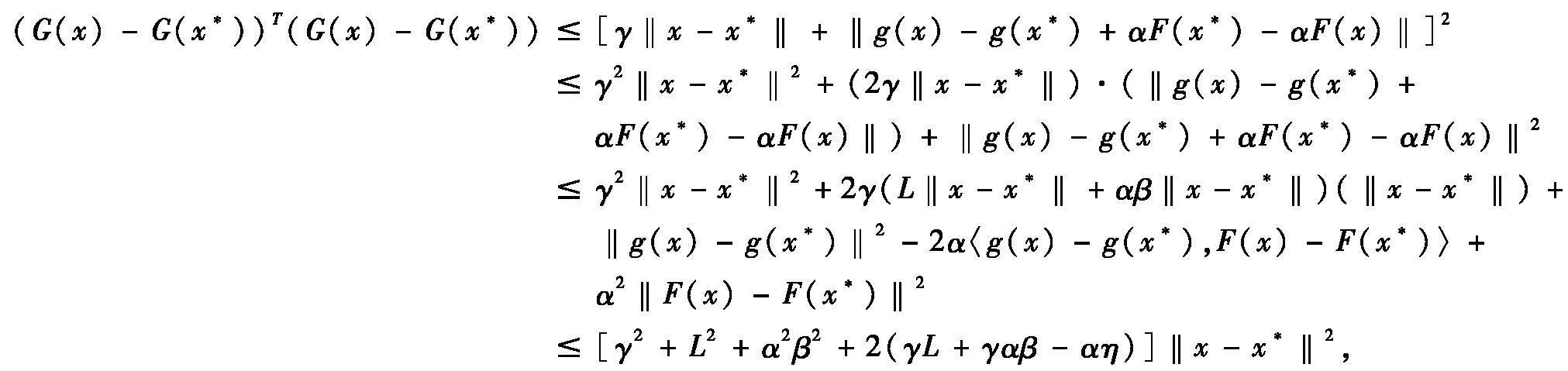
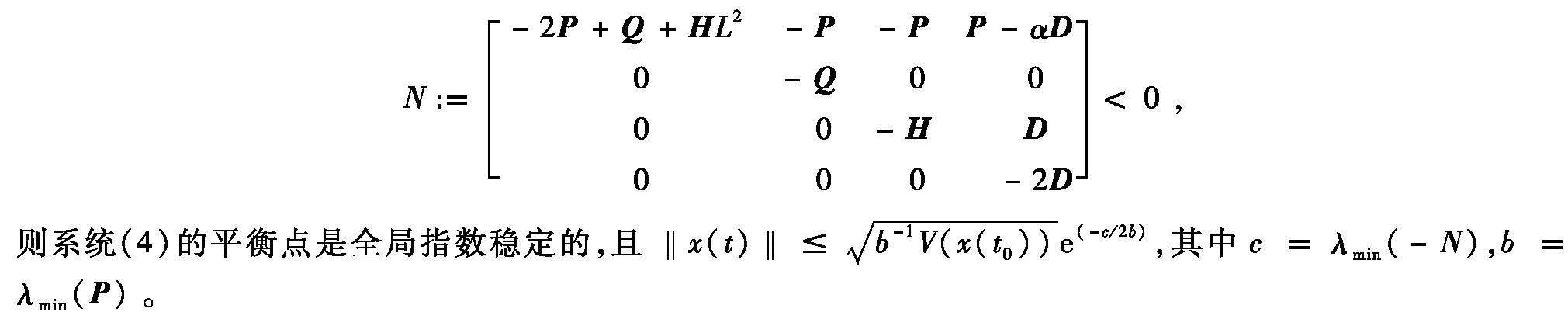
摘要：文章主要研究求解欧氏空间中逆拟变分不等式问题的一种时滞神经网络。首先，在余强制和Lipschitz连续性的条件下，利用不动点原理得到逆拟变分不等式问题解的存在性和唯一性。进一步考虑求解逆拟变分不等式问题的一种时滞神经网络，并且在强单调和Lipschitz连续性的条件下证明该时滞神经网络的全局指数稳定性。

关键词：余强制；Lipschitz连续性；强单调；逆拟变分不等式；时滞神经网络；全局指数稳定

中图分类号：O221文献标志码：A文章编号：1673-5072（2025）01-0036-06

Time-delay Neural Networksfor Solving Inverse Quasi-variational Inequalities

Abstract：In this paper，a delay neural network for solving inverse quasi-variational inequalities in Euclidean space was studied.Firstly，under the conditions of cocoercion and Lipschitz continuity，we obtained the existence and uniqueness of the solution of the inverse quasi-variational inequality problem by using the fixed point principle.Furthermore，we considered a delayed neural network for solving the inverse quasi-variational inequality problem，and proved the global exponential stability of the delayed neural network under the conditions of strongly monotone and Lipschitz continuity.

Keywords：cocoercion；Lipschitz continuity；strongly monotone；inverse quasi-variational inequality；time-delay neural network；global exponential stability

变分不等式在经济、交通、优化、运筹学和工程科学等领域有着广泛的应用，逆拟变分不等式（IQVI）是一类重要的变分不等式。2004年，Xia和Wang［1］ 提出了一种求解变分不等式的通用投影神经网络，并研究其全局指数稳定性。2012年，Noor ［2］使用投影算子技术建立了一般拟变分不等式与不动点问题和维纳-霍普夫方程之间的等价性。2020年，张从军等［3］研究了Hilbert空间中逆拟变分不等式问题，利用不动点原理得到逆拟变分不等式问题解的存在性和唯一性，利用投影技巧给出求解逆拟变分不等式的迭代算法以及误差界。2022年，常浩等［4］借助不动点理论，给出拟均衡问题解存在唯一的充分条件并考虑了一个动力系统方法来求解拟均衡问题。2023年，Dey 和Reich ［5］研究了一类拟变分不等式逆问题解的存在唯一性，考虑了相关的动力系统，并建立了该系统解的存在唯一性。

近年来，应用神经网络求解变分不等式问题已经取得很好的成果，但是在神经网络电路实现中，时滞往往是不可避免的，时滞的存在会导致系统的不稳定，但也可以改变神经网络的拓扑结构，因而可以利用时滞来改善网络动态行为，研究时滞神经网络求解优化问题更具有实际价值［6-10］。2007年，毕红梅和王婧［9］考虑了一类新的非线性变分不等式，提出了求解的一个神经网络模型，证明了该网络是Lyapunov稳定的。2014年，黄博南［10］提出一类用于求解非线性逆变分不等式问题的时滞投影神经网络模型，根据泛函微分方程理论给出神经网络平衡点的存在性和唯一性证明，根据Lyapunov稳定性理论并利用线性矩阵不等式技术和自由矩阵技术得到了神经网络是全局指数稳定的。

本文首先提出逆拟变分不等式在余强制和Lipschitz连续性的前提下，通过不动点原理证明了该问题解的存在性和唯一性。同时，考虑求解该问题的一种时滞神经网络，根据Lyapunov稳定性理论，利用线性矩阵不等式技术和自由矩阵技术，在强单调和Lipschitz连续性的条件下证明该时滞神经网络的全局指数稳定性。

1预备知识和基本概念

2解的存在性和唯一性

3时滞神经网络

下面提出一种求解逆拟变分不等式的时滞神经网络

在文献［13］中也给出了类似的时滞神经网络全局指数稳定性的定义。

由定义5可以看出，x*∈Rn是IQVI（F，g，K）问题的解，当且仅当x*是系统（3）的平衡点。

在系统（3）中，当F（x）=x且K（x）≡K，K是Rn中的非空闭凸子集，则可以退化为文献［10］提出的求解逆变分不等式的时滞神经网络，如下

则系统（3）的平衡点是全局指数稳定的，且

令（5）式为N，则上式中c=λmin（－N），b=λmin（P）。

证明考虑如下Lyapunov泛函

对以上式子进行整理可得

从而，对任意的正定对角矩阵D，都有如下不等式成立

2（G（x）－G（x*））TD（G（x）－G（x*））2［γ2+L2+α2β2+2（γL+γαβ－αη）］（x－x*）TD（x－x*）。（7）

又因为‖g（x）－g（x*）‖L‖x－x*‖，所以对任意正定对角矩阵H，都有如下不等式成立

（g（x）－g（x*））TH（g（x）－g（x*））L2（x－x*）TH（x－x*）。（8）

将式（7）和（8）代入式（6）中可得

其中c=λmin（－N）gt;0。

注释3当F（x）=x且K（x）≡K时，定理3退化为文献［10］中的结果，如下。

设g是L-Lipschitz连续的，若存在正定对称矩阵P，Q∈Rn×n，正定对角矩阵D，H∈Rn×n和正常数α，使如下的线性矩阵不等式成立

参考文献：

［1］XIA Y，WANG J.A general projection neural network for solving monotone variational inequalities and related optimization problems［J］.IEEE Transactions on Neural Networks，2004，15（2）：318-328.

［2］NOOR M A.On general quasi-variational inequalities［J］.Journal of King Saud University-Science，2012，24（1）：81-88.

［3］张从军，李杨，孙杰，等.逆拟变分不等式问题的相关研究［J］.数学杂志，2020，40（3）：341-353.

［4］常浩，冯世强，李军.求解强伪单调拟均衡问题的动力系统方法［J］.西华师范大学学报（自然科学版），2022，43（2）：170-175.

［5］DEY S，REICH S.A dynamical system for solving inverse quasi-variational inequalities［J］.Optimization，2023，90（2）：1-21.

［6］CHENG L，HOU Z G，TAN M.A neutral-type delayed projection neural network for solving nonlinear variational inequalities［J］.IEEE Transactions on Circuits and Systems II：Express Briefs，2008，55（8）：806-810.

［7］CHENG L，HOU Z G，TAN M.A delayed projection neural network for solving linear variational inequalities［J］.IEEE transactions on neural networks，2009，20（6）：915-925.

［8］HE X，HUANG T，YU J，et al.An inertial projection neural network for solving variational inequalities［J］.IEEE transactions on cybernetics，2016，47（3）：809-814.

［9］毕红梅，王婧.求解一类新的非线性变分不等式的神经网络［J］.重庆工商大学学报（自然科学版），2007，25（2）：111-115.

［10］黄博南.基于神经计算的变分不等式优化求解方法研究［D］.辽宁：东北大学，2014.

［11］FUKUSHIMA M.非线性最优化基础［M］.林贵华，译.北京：科学出版社，2011.

［12］张伟年，杜正东，徐冰.常微分方程［M］.北京：高等教育出版社，2014.

［13］LIEN C H，YU K W，LIN Y F，et al.Global exponential stability for uncertain delayed neural networks of neutral type with mixed time delays［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B （Cybernetics），2008，38（3）：709-720.