基于声发射的木材裂缝数量辨识研究

关键词：声发射； 变分模态分解； 奇异值分解； 马氏距离； 木材裂缝缺陷

中图分类号：S781. 5；S781. 38 文献标识码：A DOI：10. 7525/j. issn. 1006-8023. 2025. 01. 004

0引言

木材作为一种可再生的环保材料已经被广泛运用于生产和生活之中，但由于木材在生长、加工、保存以及运输等过程中容易产生缺陷或损伤，而缺陷的存在将会对材料的力学性质产生重要影响，降低木材使用价值，实现对木材的缺陷识别与检测一直是木材无损检测领域的研究热点之一。声发射（acoustic emission，AE）信号能够动态反映材料内部应力应变的产生和发展状况，从而为材料损伤提供了一种主动的无损检测方法［1-2］。由于木材AE信号具有非线性、非平稳的特性，所以选择合适的信号处理方法尤为重要［3］。在信号处理方面学者们也提出了很多方法，比如快速傅里叶变换（fast fouriertransform，FFT）［4］、小波变换（wavelet transform，WT）［5］、经验模态分解（empirical mode decomposition，EMD）［6］和变分模态分解（variational mode decomposition，VMD）［7］等方法。虽然以上信号处理方法能够很好地将AE信号分解成包含主要信息的分量，但是为分析AE信号的特征，需要提取各分量的内在特征，而矩阵奇异值是矩阵的固有特征，具有良好的稳定性［8］，因此矩阵奇异值符合模式识别中特征提取的要求。近年来，奇异值分解（singular" valuedecomposition，SVD）在信号降噪、特征提取等方面有广泛的应用［9-10］。除了对故障特征信息进行提取外，还需要对故障或缺陷进行识别，其中欧氏距离与马氏距离是最常用的距离度量。骆志高等［11］对金属板材拉伸过程中的AE信号提取并计算正常状态下及裂纹状态下的检验样本与各训练样本之间的马氏距离，来实现金属裂纹的识别。

当AE信号经过具有不同缺陷特征的木材时，会存在一定的差异，王明华等［12］探究了木材表面裂纹对AE信号的影响，结果发现人工裂纹主要影响AE信号的频率分布，随着人工裂纹深度的增加，AE信号的主成分频率变高，而且自然裂纹与人工裂纹中的AE信号传播速率并无明显变化。黄长林等［13］研究发现，木材AE横波能量衰减和传播速度都能够反映裂纹的存在。存在裂纹时，AE纵波的能量衰减率显著增加，而AE横波的能量衰减速率变慢，且当裂纹宽度增加时，纵波能量衰减更快，横波能量衰减更慢。Xu等［14］探究了榉木试件中不同孔洞直径与孔洞数量对AE信号的影响。麻胜兰等［15］探究了杉木在不同裂缝深度时各声发射参数的变化规律，并耦合各发射参数来检测裂缝深度。上述对木材缺陷的研究大部分集中在木材深度，并无对裂缝数量的识别。而缺陷识别的关键是特征参数的选取，现有的特征参数有小波能量矩［16］和EMD的本征模态函数协方差矩阵［17］等。小波变换过分依赖小波基的选择，EMD在分解过程中产生模态混叠和端点效应，这些会影响特征提取。VMD通过迭代搜索最优解获得中心频率和带宽，进而获得模态函数，有效抑制模态混叠。由于VMD的参数选择会影响特征提取［18］，因此选择粒子群算法（particle swarmOptimization，PSO）来确定VMD参数，避免人为参与的干扰。

本研究以樟子松为试验材料，提出基于声发射的PSO-VMD-SVD 的木材裂缝数量特征提取的方法，在此基础上用马氏距离对裂缝数量进行识别。试验中采用铅芯折断来模拟产生AE信号，铅芯折断方式参照美国ASTM-E976标准，通过对具有不同数量裂缝的樟子松试件进行试验，首先通过PSO算法确定VMD参数，并对采集的AE信号进行VMD处理，得到包含裂缝数量特征的IMF分量，然后在此基础上进行SVD，将得到的奇异值构建为能够代表裂缝数量特征的特征向量，并对不同裂缝数量特征的AE信号分别选取5组特征向量构成代表裂缝数量特征的标准特征矩阵。最后计算实测信号的特征向量与标准特征矩阵的马氏距离以实现对木材的裂缝数量的识别。

1材料与方法

1. 1试验设备与材料

研究基于NI USB6366采集卡和LabVIEW软件搭建的单通道采集系统。所选用的AE传感器为单端谐振式RS-2A传感器，其频率范围为50～400kHz，同时每个通道配备了1个40dB的前置放大器，用于放大采集的AE信号。信号的电压范围为（-10 V，10 V），由于AE信号在木材内部传播的最高频率为200 kHz左右［19-20］，根据香农采样定理，在数据采集过程中，设置采样频率为2 MHz。

试验采用的是300 mm×30 mm×100 mm（长×宽×高）的樟子松试件，在300 mm×30 mm的平面上距离左端面120 mm 处用锯片锯切出1 mm×9 mm（长×高）的裂缝，在此基础上在距离第一条裂缝右端20、40、60 mm处依次锯处同等规模的裂缝，图1表示在同一试件上不同裂缝数量的试验方案。

在实践中，依据ASTM相关标准，通常采用铅芯折断的方式产生模拟AE源，AE源距离木材表面横向中轴线的左侧60 mm，铅芯折断的方式参照美国ASTM-E976标准，选择0. 5mm铅芯，铅芯伸出长度为2. 5 mm，在距离试件表面左端面中心线上60mm处以30°的角度进行折断，且在距离左端面表面中心线上240 mm处布置AE传感器，以接收经过不同数量裂缝的AE信号，从而对经过不同数量裂缝的AE信号进行特征提取及辨识。

1. 2变分模态分解（VMD）算法及参数确定

VMD算法［21］是通过迭代搜寻约束变分模型的最优解，求解出每个分量的中心频率和带宽。VMD分解过程实际就是变分问题的求解过程，该过程主要分为变分问题的构造和求解。

VMD是将由多个成分组成的输入信号分解为K 个固有模态分量u_k （t），每个固有模态函数（IMF）都有各自的中心频率和有限带宽，并使得K 个固有模态函数的估计带宽之和最小。VMD将每个IMF定义为调幅调频函数，因此设第K 个固有模态分量的表达式为

1. 4基于PSO-VMD-SVD信号特征提取

基于PSO-VMD-SVD信号特征提取步骤如下。

1）在木材不同裂缝数量下采集AE信号，得到原始数据样本。

2）用PSO算法来确定VMD中的2个参数，然后对所采集到的原始信号进行VMD分解，得到包含裂缝损伤特征的模态分量。

3）利用VMD分解所得到的IMF分量进行SVD，获得含有奇异值序列的矩阵，取出奇异值用于构建特征向量。

1. 5基于马氏距离的裂缝数量识别方法

距离判别法是多元统计分析中一种有效的判断数据所属类别的方法，其原理为计算待测点与各类的距离，距离最短的为待测点所属分类，在距离判别法中通常使用欧式距离与马氏距离。欧式距离（euclidean distance）为空间中2个点之间的距离，但是欧式距离对数据变量间的量纲要求严格。相比于欧式距离，马氏距离（mahalanobis distance）考虑到数据各维度之间的联系，并且与维度的量纲无关，排除了维度之间的相关性的干扰。因此，选择马氏距离方法能够很方便地度量观测样本和已知样本集间的距离，适合用于对裂缝声发射信号的识别。

因此，为了对通过不同数量裂缝的AE信号进行识别，建立马氏距离判别法对采集的AE信号进行判别，首先通过上述方法计算得到待识别AE信号的奇异值向量；然后通过计算各奇异值向量与建立的各标准特征矩阵之间的马氏距离D，通过比较距离的大小，最小值为该AE信号所对应的通过裂缝的数量，从而实现裂缝数量识别的目的。

2结果与分析

2. 1确定VMD参数

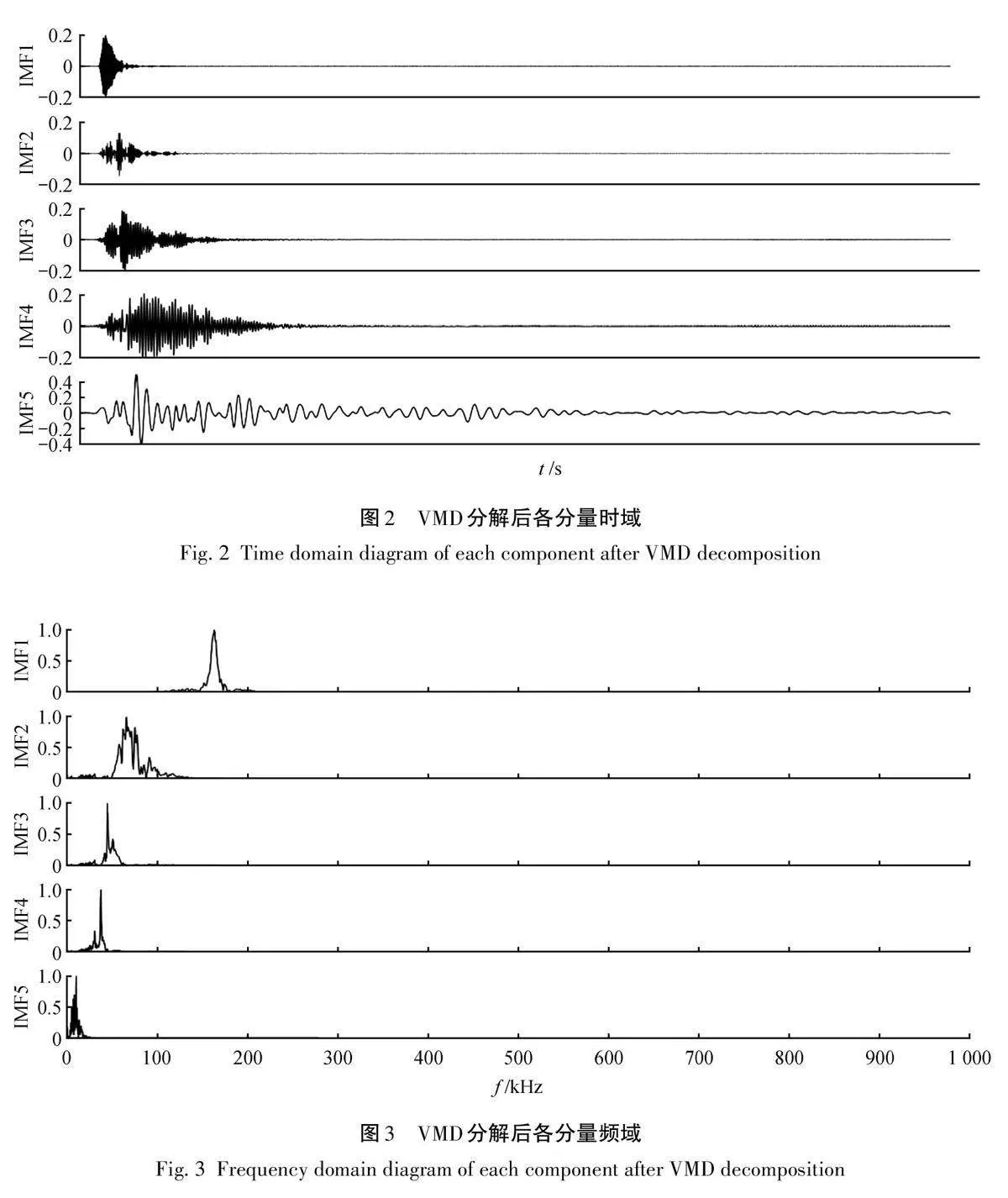
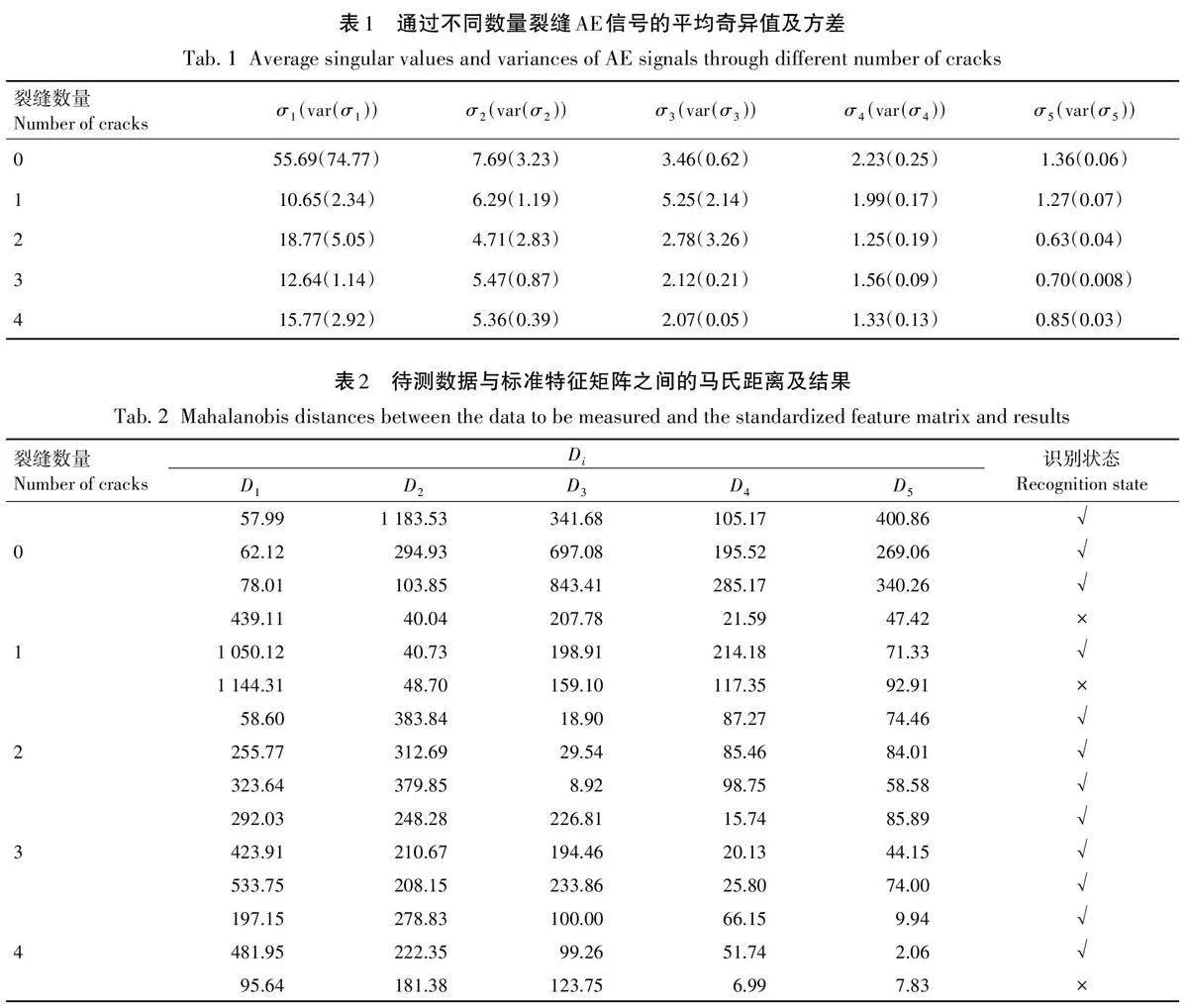
VMD算法中分解个数K 和惩罚因子α 的设置对分解结果有着较大的阴影，且AE信号在不同VMD参数分解后得到的损伤特征差别较大，PSO算法是一种群体智能优化算法，具有良好的全局搜索能力，故采用PSO优化VMD参数。PSO算法参数设置为种群数量15，模态个数K 范围[ 2，11]和惩罚参数α 范围为［500，3000］，迭代次数为50次。为确保算法稳定性，将该算法计算10次，求取模态个数和惩罚参数的平均值，得到最佳模态个数为5（IMF1、IMF2、IMF3、IMF4、IMF5），最佳惩罚参数为2 820。将优化后参数带入VMD分解得到分量时域及其频域，如图2和图3所示。

2. 2裂缝数量特征提取

为减少折铅随机性的影响以及保证试验结果的有效性，对无缝合含有裂缝的试件各进行30次折铅试验，试验共150组。随机取25组试验结果进行处理，作为标准样本，将150组试验全部作为待识别样本。

本研究对原始信号进行VMD处理，经过PSO算法筛选，VMD分解5层最为合适。利用VMD分解所得到的IMF分量构建特征矩阵，对特征矩阵进行奇异值分解，得到维度为5的奇异值序列。分别取通过不同数量裂缝的各5 组AE 信号，并对5组信号计算得到的结果进行平均，得到的平均奇异值及方差计算结果见表1，表1中var代表计算方差的函数。

由表1可知，通过不同数量裂缝的AE信号计算得到的奇异值之间存在一定的差距，无缝统计得到的AE信号奇异值方差较大，这是由于AE信号在传播过程中受到的边界效应强烈，随着裂纹数量增多导致应力波在裂纹边界处的反射增强［12］，因此会对计算得到的奇异值造成一定的影响，但说明基于VMD-SVD方法计算得到的奇异值向量可以很好地表征通过不同数量裂缝AE信号的特征，从而达到裂缝数量特征提取的目的，并将计算得到的5组奇异值向量构建为特征矩阵，作为后续裂缝数量辨识的标准特征矩阵。

2. 3裂缝数量辨识

分别对150组待检测数据进行VMD-SVD处理计算其特征向量，并按照1. 5中的方法计算实测数据的特征向量与各标准特征矩阵之间的马氏距离Di，依据最小判别原则，分别比较各距离的大小，最小值所对应的类别即为测试样本所属类型。马氏距离计算结果见表2（限于篇幅，列出部分）。

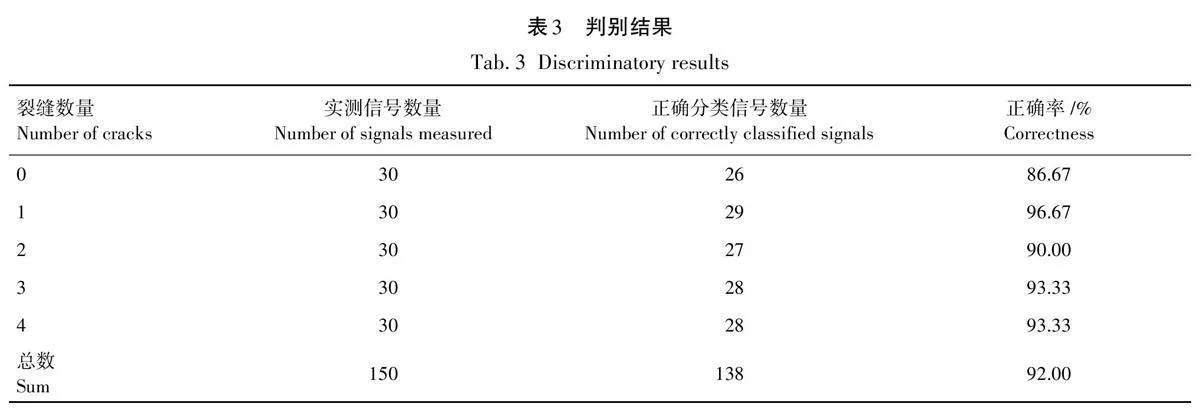
由表2可知，马氏距离计算结果之间有较大差异，这是因为马氏距离的计算依赖协方差矩阵，而协方差矩阵的选择是随机的，造成马氏距离计算结果的差异性，但不影响辨识结果。而实测信号与其所属类别的标准特征矩阵之间的马氏距离比其他的要小，虽然存在误判的情况，但是整体呈现出较好的准确性。通过统计，待测数据的判别结果见表3。

由表3可知，对150组数据进行判别，判别正确的数据有138组，正确率达到92%，说明了通过PSOVMD-SVD对通过不同数量裂缝的AE信号进行处理能够很好地表征木材裂缝数量特征，且在此基础上通过计算马氏距离能够很好地识别木材中裂缝的数量。

3结论

针对木材裂缝损伤，在折铅试验的基础上通过PSO-VMD-SVD和马氏距离结合的方法，对裂缝数量进行特征提取以及通过计算待测样本的特征向量与标准样本所建立的标准特征矩阵之间的马氏距离对木材裂缝数量进行识别。

VMD是一种自适应、完全非递归的模态变分和信号处理的方法，将样本熵作为PSO 的适应度函数，实现对VMD参数的快速有效搜索，提高VMD对非平稳振动信号分解的自适应能力，并有利于损伤信号的特征提取。试验中，通过对原始AE信号进行5层VMD分解，SVD方法构建的奇异值特征向量能够准确表达不同裂缝数量信号的特征。通过计算150组待判别数据与各标准特征矩阵之间的马氏距离对裂缝数量进行判别，结果判别正确率达到92%，结果表明，通过PSO-VMD-SVD处理之后得到的奇异值向量可以很好地表征木材裂缝数量特征，并通过计算马氏距离，实现对裂缝数量识别。

由于试验以人工切割裂缝的方式开展研究，与真实裂缝存在一定偏差，且试件数量有限，检测准确度还有待进一步提高。