一维准周期镶嵌模型的扩展态

摘" 要：最近的理论研究发现，一维准周期镶嵌模型存在迁移率边。在该文中，研究该模型的量子输运，尤其是扩展态的两端口电导，模型的输运相图、平均值和统计分布。扩展态的电导并不恒为1，而是有干涉共振条纹，用波函数的行为解释这些干涉条纹。该模型的扩展态能在极强的准周期势能下存活，通过电导的统计分布，以及与波函数分形维度的比较，解释其中的物理图像。

关键词：准周期镶嵌模型;扩展态;电导;介观输运;量子输运

中图分类号：O413" " " 文献标志码：A" " " " " 文章编号：2095-2945（2024）26-0032-06

Abstract： Recent theoretical studies have found that there is a mobility edge in the one-dimensional quasi-periodic mosaic model. This paper studies the quantum transport of the model， especially the two-port conductance of the extended state， its transport phase diagram， average value and statistical distribution. The conductance of the extended state is not always 1， but there are interference resonance fringes. We explain these interference fringes by the behavior of wave function. The extended state of the model can survive under extremely strong quasi-periodic potential energy. Explain the physical images through the statistical distribution of conductance and the comparison with the fractal dimension of wave function.

Keywords： quasiperiodic mosaic model; extended state; conductance; mesoscopic transport; quantum transport

量子输运是量子相干效应明显时发生的输运现象，其可以发生于低温的普通晶体材料中，也可以发生于光子晶体等现代量子材料中。量子输运是微观粒子（如电子）的波函数经历晶格和杂质相干散射的结果，因此晶体的细节，例如周期性或非周期性都会对量子输运产生很大的影响。根据标准的固体能带理论，周期晶格中的波函数都是扩展的布洛赫波，有良好的导电性。然而，无序会破坏晶格的周期性，同时影响波函数的扩展性。这个影响与系统的空间维度密切相关[1-2]。在三维晶格中，弱无序不会改变波函数的扩展性，但强无序会导致金属-绝缘体相变（或叫“扩展态-局域态转变”），能量轴上的相变点称为迁移率边。不过，在一维或二维晶格中，任何有限的无序都会使波函数局域化，从而导致全部状态都处于绝缘相[1-2]。这些都是凝聚态物理中熟知的结论。

准周期结构微妙地介于无序和周期之间，是传统固体电子理论较少研究的对象，其对量子态的影响是现代凝聚态物理感兴趣的话题。近期最著名的准周期结构出现在转角石墨烯中，两层石墨烯之间存在一个非公度角度的时候，晶格形成准周期结构[3-4]。这个二维准周期结构会在狄拉克点附近形成平带，从而有助于超导、强关联等丰富物理现象的发生。

在一维系统中，准周期对波函数的作用也是近期的一个研究热点[5]。在著名的Aubry-André-Harper模型（简称AAH模型）中，人们在一维紧束缚模型上施加了一个周期势，但其周期与晶格的周期不公度，从而构成准周期势。理论研究发现，如果准周期势足够弱的话，即便在一维也能出现扩展态[6]。当准周期势能大于临界值后，本征态会被局域化。但这个模型中的扩展态-局域态转变对能量轴上的所有本征态是同时发生的，因此没有迁移率边。

最近，Wang等[7]对AAH模型进行了改进，设计了一个被称为镶嵌模型的一维结构，即周期性（周期大于1）地让格点的势能为零。这个看似简单的改变就能让系统出现迁移率边：能带中心为扩展态，能带边缘为局域态。

在本论文中，对这个镶嵌模型的量子输运进行了更细致的理论研究，尤其是其中扩展态（即金属态）的行为。计算了该模型不同参数下的分形维度和两端口电导，并详细讨论了其统计涨落和尺寸标度效应。研究发现扩展态确实对应着非零的电导，但电导的行为有很多有趣的细节，例如干涉共振起伏与波函数的关系。在能带中心，该模型的扩展态可以在非常大的势能强度下存活，但这个过程中，其能带结构和电导的统计性质会有对应的改变。我们分析和解释了扩展态的特征。

1" 模型和方法

许多原来只出现在理论研究中的一维晶格模型，目前已经能够通过冷原子、光晶格等现代实验方法实现。其中的周期、无序或准周期结构也能够通过越来越成熟的技术进行设计和调控。在本文中，考虑一维晶格中的准周期镶嵌模型，其紧束缚哈密顿量可以描述为[7]

H=t（cc+H.c.）+2λjnj ， （1）

式中：c（cj）是费米子在第j个格点处的产生（湮灭）算符;nj是该处的粒子数算符（或势能算符）。t是最近相邻格点的跳跃系数，把其设为1作为能量单位。同时把晶格常数（最近邻格点间的距离）设为1作为长度单位。λj是第j个格点上的准周期镶嵌势能，由下面的式子给出

λj=λcos[2π（ωj+θ）]，j=mκ

0，其他， （2）

式中：λ是势能的强度，θ是势能的空间初相位。参数ω决定了势能的周期，如果其是无理数就能保证势能周期与晶格周期非公度，形成研究的准周期势能。如无明确指出，设置θ和ω的值分别为： θ=0，ω=（-1）/2。κ是决定镶嵌调制周期的整数，当κ=1时，即为最初的AAH模型，不具备迁移率边。当κ≠1时，此时模型有镶嵌，即可出现迁移率边[7]。本文中κ=2。取 m=1，2，...，N，此时系统长度为L=κN。对于这个模型，文献[7]中已经给出了不同势能强度时候的迁移率边为Ec=±1/λ，也就是说，当能量|E|小于1/λ时，本征态处于扩展态，而|E|大于1/λ时的本征态处于局域态。有了哈密顿量，就可以通过标准的对角化方法求得本征能量和相应的本征态。为了表征本征态的局域化性质，引入逆参与率（IPR），其定义式为[7-8]

IPR（m）=Ψm，j， （3）

式中：Ψm，j表示第m个本征态。典型的扩展态和局域态分别对应着IPR接近0和1。通过IPR还可以定义另一个更直观的量，即分形维度，表达式如下

Γ=- 。 （4）

在一维晶格中，趋于0和1分别对应局域态和扩展态。

以上物理量研究的都是孤立晶格中波函数的性质。波函数的局域化程度会直接影响量子输运。设想把一定长度的该模型晶格（即研究对象）接上电极，就可以测量其电导。在零温时，可以利用著名的Landauer 公式来模拟计算此时的电导，其正比于费米子的量子透射率，用格林函数表达是[9-10]

（5）

式中：e是电子电荷;h是普朗克常数;τ是透射率;ES是测量时研究对象中的费米能。ΓL和ΓR分别是左右电极的谱函数矩阵，其计算公式为

ΓL/R（Elead）=i（ΣL/R （Elead）-Σ（Elead），（6）

式中：ΣL/R（Elead）是描述左右电极自能的矩阵;Elead是电极中的费米能。Gr（E）和Ga（E）分别是推迟和超前格林函数，计算公式为

Gr/a（E）=[E-H-Σr/a（Elead）]-1，（7）

式中：H为研究对象的哈密顿量;E为本征能量。

实验中测到的电导是经历了多个相位相干长度后的平均结果，这在无序系统中相当于取了不同的无序构型进行平均[11-12]。在这里的准周期结构中，为了类比无序系统中的无序构型样本，在其他关键模型参数取定的情况下，采用2种抽样和平均方式。第一种是在公式（2）中取一组随机的θ，简称为“相位平均”。第二种是在公式（5）中取一组随机的电极费米能Elead，简称为“能量平均”。这2个参数的改变都能导致电导的涨落。然后就可以得到相应电导的平均值、方差和统计分布，从而获得量子输运的更丰富信息。

2" 结果和讨论

首先来研究孤立体系的性质，即本征波函数的分形维数。由之前的介绍得知，当分形维度Γ趋于1时，模型处于扩展态，这引发了笔者对于分形维度与样本长度之间关系的深入探讨。

在图1中，取势能强度λ=1，画出了本征函数的分形维度Γ作为本征能量E的函数，不同形状的点代表了不同的样品长度。由于计算结果对于能量原点是对称的，因此只画了正能量部分的结果。图中第一个明显的特征是：本征能量的分布并不完全连续，而是被分割成了几个子能带。这是镶嵌势能的一个特点[7]。

现在仔细观察数值点的细节。可以看到，在迁移率边Ec=1的两侧，分形维度的尺寸标度确实具有不同的特征。在迁移率边左侧的本征态，其分形维度数值都随着尺寸N的增加而增大。例如，菱形数据点（N=25 600）位于圆形数据点（N=400）的上方。因此可以预见在热力学极限N→∞时，分形维度将趋于1，显示出明显的扩展态行为。另一方面，在迁移率边右侧的本征态，其标度行为则是相反的：菱形数据点（N=25 600）位于圆形数据点（N=400）的下方，也就是分形维度随着尺寸增大而减小，从而在热力学极限下趋于0，显示出标准的局域态行为。

以上是一个固定λ值时孤立体系的波函数局域化性质，应证了解析计算的结果。现在转到输运性质。在图2中，画出了平均电导随着样品能量与势能的变化的相图。图2（a）、图2（c）、图2（e）表示电极能量EL的平均的结果，图2（b）、图2（d）、图2 （f）表示相位偏移θ的平均的结果。图2（a）、图2（b）中的Nx=1 000， 图2（c）、图2（d）中的Nx=2 000，图2（e）、图2（f）中的Nx=4 000。图中的浅色和深色分别代表电导接近1和0。首先可以看到，2种平均下亮色的区域都是一致的，而且这些区域的范围并不随着长度增长而缩小，因此代表了稳定的扩展态。这些扩展态的分布区域与分形维度[5]的计算结果一致。因此，量子输运确实忠实地体现了波函数的性质。

Nx=1 000，2 000，4 000，朗道电导的平均值L作为样本中心能量ES和准周期势强度λ的函数，图2（a）（c）（e）表示电极能量EL的改变，图2（b）（d）（f）表示相位偏移θ的改变。

进一步观察发现，浅色区域的电导尽管都远大于0，但并不都等于1，而是有起伏，形成精致的干涉共振条纹。其中最显眼的是ES=0的中心线上的浅色的点，代表了最明显的共振峰。在相同长度的情况下，共振峰的位置对2种平均都是相同的，但共振峰的个数随着长度的增长而增加。

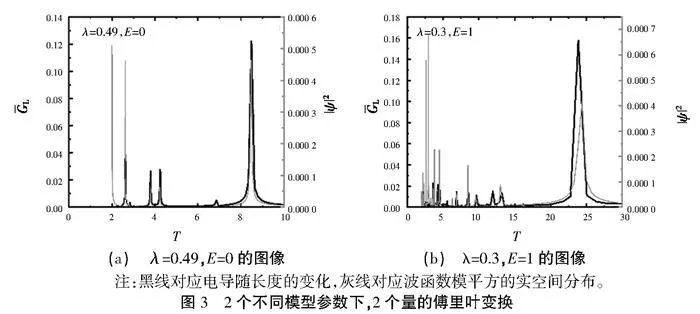
为了更好地理解电导和波函数之间的对应关系，例如图2所示的共振峰的来源，比较实空间波函数的起伏。与电导随长度变化的关联性。为了反映波函数对于样品空间的依赖细节，选取一个位于扩展态区域的本征能量，计算波函数模平方的傅里叶变换，其包含了波函数实空间涨落的特征性信息。与此同时计算该样品处于这个费米能时，电导作为样品长度的依赖关系，并且对其也作傅里叶变换。在图3中，选取了2个典型的能量，分别用黑线和灰线画出了这2个量的傅里叶变换。可以看到，2条曲线在多数情况下具有相同的峰值位置，这就说明了电导的起伏确实来源于波函数的起伏，两者是高度相关的。剩下有少数峰值不相关，可以归结为样品边界的散射影响，因为计算波函数时采用的是固定边界条件，但计算电导时样品边界则连着半无限电极。这2种不同边界对波函数的散射，会导致一些不同的相干空间涨落，于是形成不同的傅里叶峰。

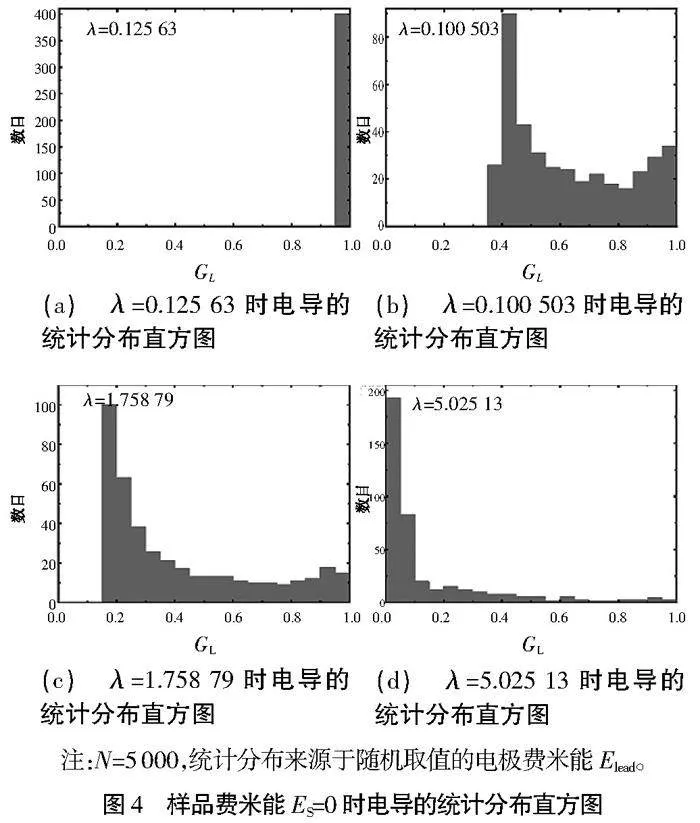
上面讨论的是电导的平均值，现在来研究其统计涨落。众所周知，电导的统计性质与局域化性质密切相关[2，11-12]。在图4中展现了电极能量改变时电导的统计直方图，4个子图对应着依次增大的势函数强度λ。在图4（a）中，极弱势能时（λ=0.125 63），电导集中分布高度集中在接近1的区域，也就是接近完美透射的扩展态。随着势能增大，如图4（b）和图4（c）所示，电导分布逐渐展宽，直到占满区间（0，1）。与此同时，统计分布的重心往低电导方向移动。最后，强势能时，如图4（d）所示，电导出现一个峰值接近0的长尾分布。此时尽管电导的平均值比较小，但即便在很长样品的情况下（例如N=100 000）这个平均值仍然不是0，而且时不时还会出现一些电导远大于零的统计样本。这对于只有一个通道、背散射风险很大的一维时间反演模型已经非常不容易了[2，11]。总之，此时系统仍然处于良好定义的扩展态。与此相反，在|E|gt;1/λ时的局域态，即便在弱势能、样品长度不大的情况下，所有统计样品的两端口电导都非常接近零了。

对于周期系统，良好定义的能带结构与输运性质之间有良好的对应关系[2-3]。虽然严格来说，准周期结构不具备周期性，但仍然可以用周期结构来逼近准周期结构，如斐波那契结构[5，8]，从而获得能带结构。为了更加深入地理解不同势能强度下输运特性与量子态的内在联系，利用斐波那契晶格来计算准周期势能系统的能带结构，具体计算方法如下。取一个长度为第n个斐波那契数Fn的样本，即L=Fn，此时取公式（2）中势能的周期参数ω=ωn=Fn-1/Fn，其是一个有理数。于是就可以以这个长度为Fn的样品作为超元胞，按照标准的傅里叶变换来计算能带结构，即色散关系E（k）。当n趋于无穷时，ωn也趋于无理数（-1）/2，从而使得样品趋于本文研究的准周期势模型[5，8]。

图5就是按照这种方法计算的能带结构，超元胞长度L=F17=1 597。只画出了关心的能带中心附近的几个子能带。4个子图分别对应着图4中4个子图的势能强度λ。在图5（a）展示的弱势能情形，子能带显示出接近线性的色散关系，并且子带之间的子带隙非常小。根据Thouless公式，电导正比于群速度（即色散关系的斜率）与态密度的乘积[13]。因此，图5（a）中的这种能带结构，即接近于常数的群速度与极小的带隙，在2个因素上都有利于形成较大的电导，并且携带较大电导的本征态稠密地分别在能量轴上。这就是本文在前面的图4（a）中看到的现象。

随着势能的增强，在图5（b）—图5（d）中，子能带变得越来越平，子带隙也变得越来越大。这种变化趋势可能会导致量子态的输运能力下降。但是，系统通过2个方面的努力来让自己避免被完全局域化。首先，子能带在强势能的时候虽然被压制得很窄，但其宽度并不是零，这与局域态有数量上的明显差别。其次，子能带之间变得更密集（阻止态密度过度降低），以此来弥补群速度降低而给Thouless电导带来的损失。因此在强势能情况下，最后的总效果就是，能带中心仍然存在着扩展态，但扩展态之间的子带隙仍然比弱势能情况下的更大。这就导致一个现象：当费米面穿过顽强的子能带时，电导远大于0;当费米面穿过子带隙时，电导接近于0。这就造成了在图4（b）—图4（d）中显示的电导涨落增强。

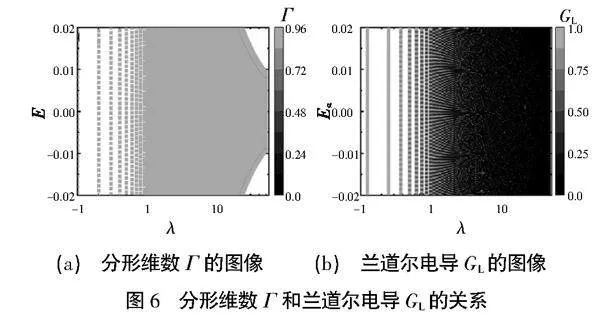
上面这个物理图像，还可以在更强的势能强度下得到进一步的印证。可以看到，在准周期势λ远大于带宽的情形下，这个一维模型在ES=0附近仍然存在扩展态，这是比较特别的。为了更清楚地看到大λ情况下发生了什么，在图6中画出了E=0附近的分形维度（图6（a））和电导图（图6（b）），但扩大了λ的扫描范围。从图6（a）的分形维度可以看到，数值接近1的扩展态（浅灰色）在λ接近100的情况下仍然非常顽强地存在着。但与此同时，图6（b）的电导在λ不到10的时候就接近0（黑色），似乎变成局域态了。但放大后就能看到，此时是在黑色（电导接近0）的海洋里点缀着浅灰色（电导接近1）的孤立点。

这些现象再一次反映了在图4和图5中看到的物理图像。扩展态能带分裂为多个扩展态子能带。随着λ的增加，子能带逐渐变窄，它们之间的子带隙则变宽。于是，当扫描能量的时候，如果扫到了子能带里，就能得到电导接近1;如果扫到了带隙，就得到电导接近0。这就是图3中电导分布越来越宽、平均值越来越接近0的原因。但无论如何，只要能量在子能带里，电导就不会是0，因此也仍然是良好定义的扩展态。有理由相信，在λ趋于无穷时，仍然会在ES=0附近存在一个无限细的扩展态子能带。

3" 结论

本文研究了一维准周期嵌套模型的量子输运性质，得到以下结论。

1）扩展态的电导不为零，且具有随着能量和势能强度改变的干涉共振起伏。这些起伏的大部分都与波函数的起伏对应，少部分来源于界面处的反射与干涉。

2）在主能带中心，随着势能增长，扩展态一直存在，但能量分布范围缩小。这种分布可以缓解由于子能隙扩大而导致的态密度下降，并弥补子能带变平而导致电导的过度下降。

3）在此过程中，电导的涨落逐渐增大，平均值也在降低，但不为零。原因是扩展态子带的带宽逐渐变小（但不会变为零），子带隙逐渐变大。于是当费米能碰到子带（带隙）的时候就表现为接近1（0）的数值。

参考文献：

[1] E. ABRAHAMS， P.W. ANDERSON， D. C. LICCIARDELLO， et al.. Scaling theory of localization： Absence of quantum diffusion in two dimensions[J].Phys.Rev.Lett.42，673 （1979）.

[2] P. A. LEE， T. V. RAMAKRISHNAN. Disordered electronic systems[J]. Rev. Mod. Phys.57，287（1985）.

[3] B. BISTRITZER， A. H. MACDONALD. Moiré butterflies in twisted bilayer graphene[J].Phys. Rev. B 84，035440 （2011）.

[4] Y. CAO， V. FATEMI， A. DEMIR， et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices[J]. Nature 556，80（2018）.

[5] A. JAGANNATHAN. The Fibonacci quasicrystal： Case study of hidden dimensions and multifractality[J]. Rev. Mod. Phys. 93，045001（2021）.

[6] S. AUBRY， G. ANDRÉ. Analyticity breaking and Anderson localization in incommensurate lattices[J].Ann. Isr. Phys. Soc. 3，133（1980）.

[7] Wang Y， Xia X， Zhang L， et al. One-dimensional quasiperiodic mosaic lattice with exact mobility edges[J]. Phys. Rev. Lett.125，196604 （2020）.

[8] WANG Y， ZHANG L， SUN W， et al. Quantum phase with coexisting localized， extended， and critical zones[J]. Phys. Rev. B 106，L140203 （2022）.

[9] S. DATTA. Electronic transport in mesoscopic systems[M]. Cambridge： Cambridge University Press， 1995.

[10] S. DATTA. Quantum transport： Atom to transistor [M].Cambridge： Cambridge University Press， 2005.

[11] F. EVERS，A. D. MIRLIN. Anderson transitions[J]. Rev. Mod. Phys. 80， 1355 （2008）.

[12] LUO X，T. OHTSUKI. Universality classes of the Anderson transitions driven by quasiperiodic potential in the three-dimensional Wigner-Dyson symmetry classes[J]. Phys. Rev. B 106，104205 （2022）.

[13] J. T. Edwards，D. G. Thoules." Numerical studies of localization in disordered systems[J]. J. Phys.C 5，807 （1972）.

基金项目：广东省自然科学基金（2023A1515010698）

第一作者简介：张彪（1997-），男，硕士研究生。研究方向为量子输运。

*通信作者：张艳阳（1978-），男，博士，副教授。研究方向为量子输运。