让学生“带得走”的寻理数学

初遇“寻理”，是在2016年12月执教公开课“用字母表示数”。那次的备课、试教，让常年不上课的我收获了久违的酣畅淋漓之感。学生兴致盎然，全情投入，错着、逗着、乐着就下课了。事后，我一次次回想、反思当时的场景，忽然领悟，数学课堂是需要情理相融的，用富含情趣又能蕴含学科意图的情境激发学生提出自己的问题，引导他们经历自己的寻理过程，再由低到高按序展示他们的思维作品，让这些思维作品形成课堂中天然的“‘趣点’和‘思点’”，“在这个过程中，低阶思维给予高阶思维观察、反省的机会，高阶思维则给予低阶思维促动、生长的可能”[1]，以此，促成学生“寻理”活动的深入展开。后有幸得到南通市教科院冯卫东先生的指点，把“情理”改成“寻理”，顿觉意蕴的灵动与神妙。

“学习数学唯一正确的方法是让学生本人去发现或创造出要学的东西，教师的任务是引导和帮助学生进行这种再创造的工作。”当我读到弗赖登塔尔的这句话时，更是坚定了践行“寻理数学”的信心。

一、“让学生‘带得走’的寻理数学”内涵

1.学生“带得走”：主要指不随知识的遗忘而被剥离，能够陪伴学生行走，能够不断“发酵”给予学生能量的思想、方法、能力及情感态度。“带得走”，其实质是“形成和发展学生面向未来社会和个人所需要的核心素养”[2]。

2.寻理数学：理，原指物质组织的条纹、纹理，这里代指数学学科的原理、算理、学理及理性思维、理智洞察、理性精神。寻，是追寻、寻求、寻根究底，这里兼有“询、循、巡”之意。寻理数学，是指学生在课堂学习中自主地探寻学科原理；在活动中学会“询理”（互相质询、追问）而进，“循理”（遵循学科之理、逻辑之理）而为，最后抵达“巡理”（巡探究路径、巡推理步骤、巡以往经验）而构。

3.让学生“带得走”的寻理数学：让学生“带得走”，是教育的终极期待；“寻理数学”是其路径架设。让学生“带得走”的寻理数学，是指在适切的问题情境激发、调整下，学生自主地展开寻理式学习探究过程，通过其思维的碰撞、认知的迭代，走向数学之“理”的通透、数学理性的通达、学习之理的概括，从而获得能够“带得走”的、足以观照其后续发展的思维方法、行为习惯、理性精神及情感态度。

二、“让学生‘带得走’的寻理数学”实施路径

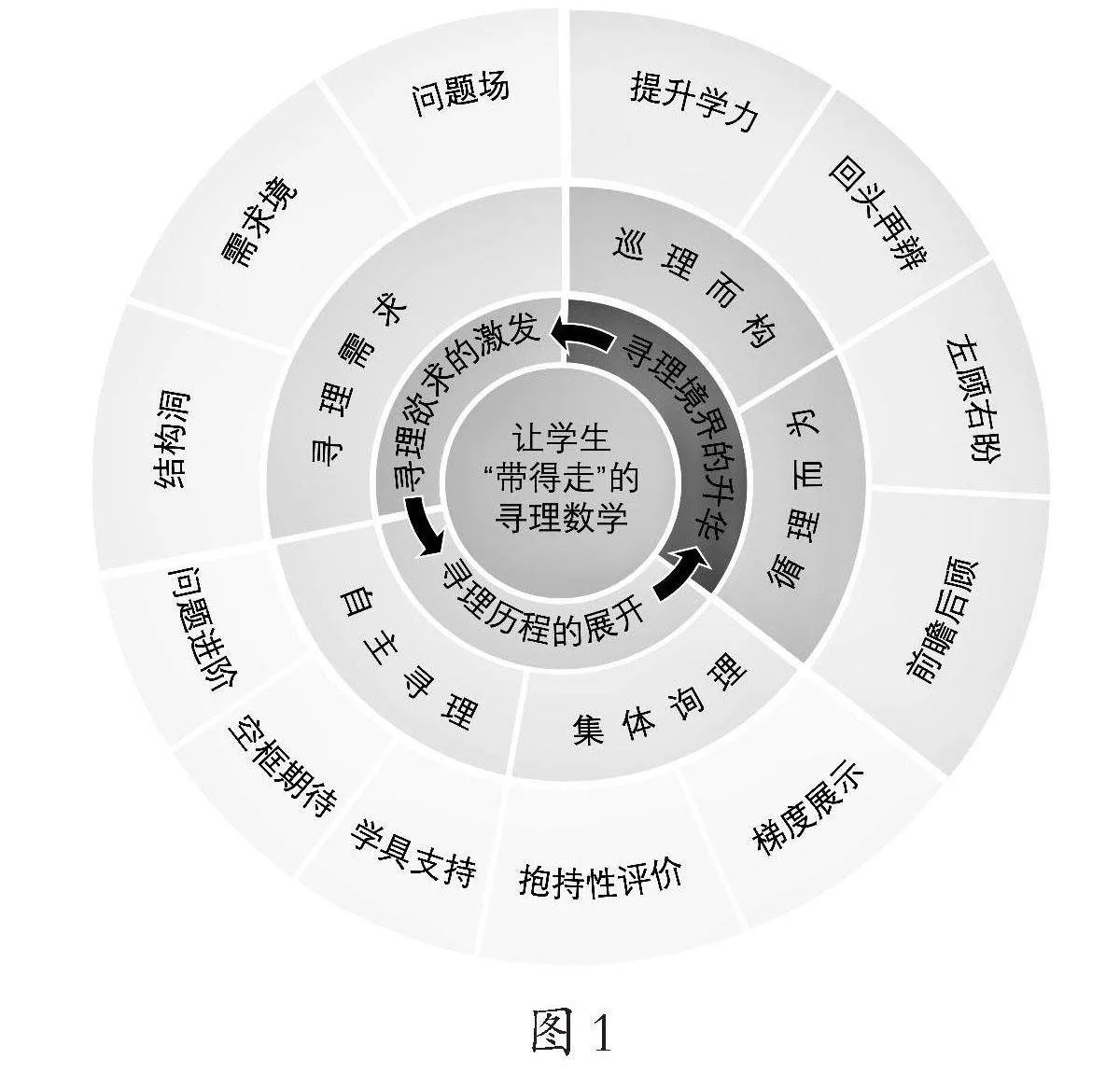
让学生“带得走”的寻理数学，实施流程是：寻理欲求的激发、寻理历程的展开、寻理境界的升华（如图1）。这是一个循环往复的过程。

1.寻理欲求的激发。

寻理欲求的激发，即教师立于学科视角的高位，知晓学科知识的历史发生、发展的过程，用数学的眼光观察儿童的学习，再用儿童的眼光观看数学，在“学科要求”和“儿童需求”之间找到适切的共振点，设计出“蕴含学科意图又不失其情趣”的问题情境，激发儿童提出自己真实的、又是学科需求的问题，让儿童有问需寻。

2.寻理历程的展开。

寻理历程的展开，始于个体寻理，深化于集体询理。

个体寻理，即学生自主展开独立的寻理过程。师“退”生进，教师通过支持性学材的创设，让儿童有能力投入长程的自主寻理过程，有机会收获惊喜，增强自信，提升对数学的兴趣。

集体询理，即借助班级授课制下生生之间思维层次的落差，通过抱持性评价，（抱持：心理学家温尼科特提出的经典术语，意思是“接纳和支持”）引出学生个性思考的多样化，再通过“梯度展示”，让学生拾级而上，深化“数学的‘再创造’”，促成雅斯贝尔斯所描述的理想教育情形：“一棵树摇动另一棵树，一朵云推动另一朵云，一个灵魂唤醒另一个灵魂。”

3.寻理境界的升华。

寻理境界的升华，是学生经历个体寻理和集体询理后的再一次出发，通过循理而为和巡理而构实现。循理而为，让学生在独立解决问题过程中，展现其学科理解的通透度、推理过程的逻辑性、言语表达的精准度、知识运用的灵活性。巡理而构，是经过一段时间学习后，学生自主地巡理回望。在回望里，提升认知、提炼思维方法、萃取活动经验、优化认知结构、提升个体的学习力。

三、“让学生‘带得走’的寻理数学”的教学策略

1.寻理欲求的激发策略。

“如果你想造一艘大船，不要召集人们去堆积木料，也不要向他们布置任务和工作，而要激发他们对浩瀚无垠大海的向往。”（《小王子》）心理学研究表明，最强烈且持久的动机来自内在的自主动机。教师可以通过“需求境”“问题场”“结构洞”，激发学生自主的寻理欲求。限于篇幅，笔者在此略述“需求境”的创设、“结构洞”的挖掘。

（1）需求境：寻“学科要求”与“儿童需求”的共振点，让学生有需而寻。

苏教版教材五年级下册的“折线统计图”的教学，我选取的主题是“身高的秘密”。因为五年级的儿童，年龄为10～11周岁，女生、男生正陆续进入身高增长的第二个关键期（女生大约10～14岁；男生略晚两年）。每个人都期待明天的自己能够长得高一些，而这时，研究身高增长的规律，用规律调理当下、塑造明天更好的自己，正是学生潜在的强烈需求。在这样的需求下，有利于展现身高变化规律的统计工具——折线统计图，就一步步地应需而生了。

（2）结构洞：在认知结构中引出冲突，让学生有问需寻。

一直记得俞正强老师“笔算除法”中的片段：首先，俞老师为三年级学生塑造了一个憨厚可爱的二年级学生形象，让三年级学生用安全的心态看二年级学生的问题；然后，俞老师在黑板上记下“二年级学生”的理由：因为

，所以

。

一瞬间，所有学生的眼睛都亮了，这也是他们一直深埋心底的问题，只是不敢说出来。现在，这个“二年级学生”的问题让他们发现：他们曾经小心翼翼埋藏的问题其实是合情合理的，甚至是了不起的。“为什么要变换除法笔算的书写方式呢？”他们内在的探索欲被重新唤醒、强烈激发。

2.寻理历程的展开策略。

寻理历程在个体寻理中展开，在集体询理中进阶。

（1）个体寻理，学材扶助中深入。

学生个体的寻理，是在教师精心创制的学材辅助下，有所侧重地探究。好的学材，能把教师的有为隐于无形，既给予学生足够的操作支持和思维支撑，又不暗含指示，束缚学生的思维。寻理数学目前开发的学材类型有：逐层进阶式的主线性问题、引出儿童真实的空框式作业单、指向学科本质的支持性学具等。

①逐层进阶式的主线性问题。

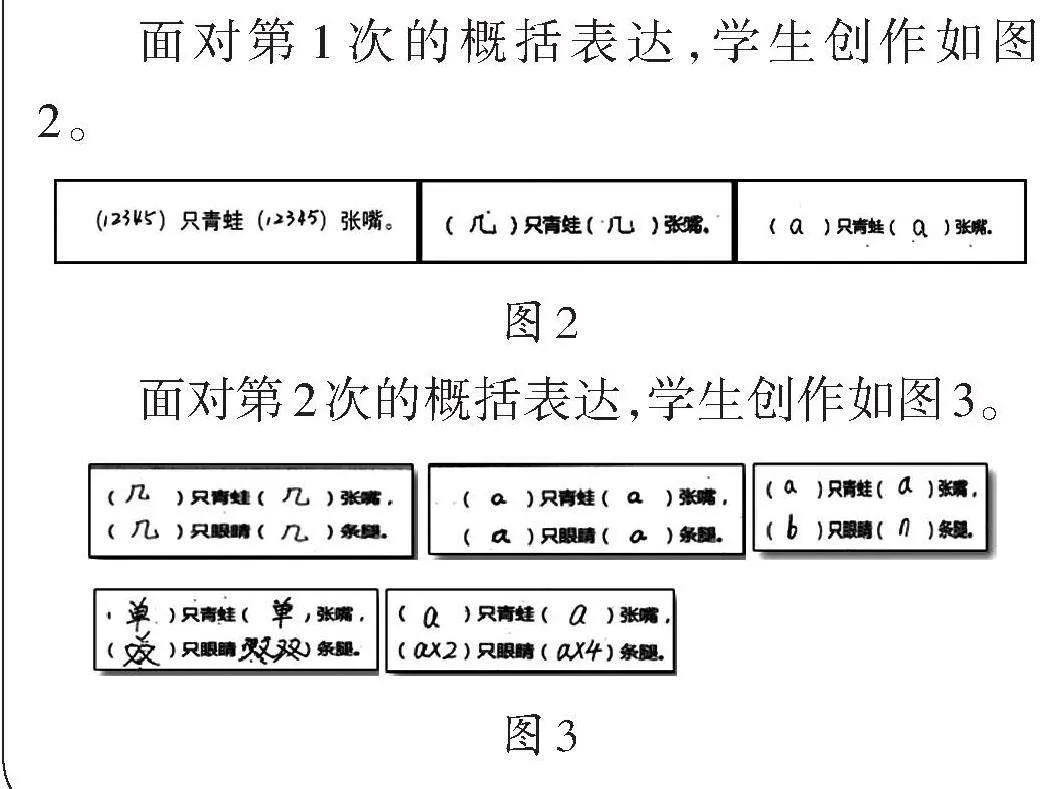
主线性问题，免去情境切换引发的注意力耗损；逐层进阶，让不同认知水平的儿童都能在过程中感知自我效能感，提升独自寻理的勇气和兴趣。在“用字母表示数”一课中，我选择了“青蛙歌谣”导入，并把它分成两阶段展现：第一阶段，“1只青蛙1张嘴，2只青蛙2张嘴……”，促发学生“概括表达一类数”的需求，并在尝试中初步感知表达的方法；第二阶段，“1只青蛙1张嘴，2只眼睛4条腿；2只青蛙2张嘴，4只眼睛8条腿……”，感悟“表达一类数”“表达不同的一类数”“表达有关系的不同的一类数”之间的区别与联系，体会字母表达数的独有价值。

②引出儿童真实的空框式作业单。

空框式作业单，引导学生把内在的、隐性的思考转化为可触摸、观察、评论的“作品”，“只有表现理解，才能发展理解”[3]。在“用字母表示数”中，我交给学生一份印着空框的作业单。

面对第1次的概括表达，学生创作如图2。

面对第2次的概括表达，学生创作如图3。

用“空框”，表达教师对学生的信任，放下思维的掣肘；用“空框”，拓宽学生自我创意的空间，让学生遵循自我的内心做真实的探寻。当学生的自我创意得到表达、交流、对比时，思考就自然拔节。

③指向学科本质的支持性学具。

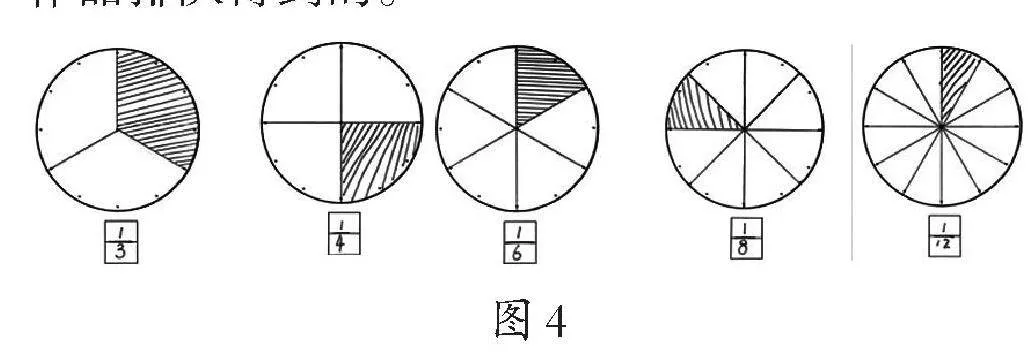
好学具，能把学生从“动手操作”有效地引向“认知活动”，既有利于操作，又直指学科本质。在“分数的初步认识”创造几分之一的环节，我调整了让学生对折圆形纸片的方法，设计了类似钟面的圆形图，让学生分一分、画一画，做出自己想要的几分之一。

画线均分比对折的速度慢了许多，却需要带着“平均分”的眼光动手操作，且打破了对折中仅出现2、4、8等份数的局限性；画线比折痕也清晰得多，让学生可以清晰地看见“分母”“分子”，加深对几分之一的认知。由此进一步看见几分之一的大小，如图4，就是学生手持自己的作品排队得到的。

（2）集体询理，生生互启中进阶。

集体询理，通过“抱持性评价”和“梯度展示”达成。

①抱持性评价。

“抱持”，即接纳与支持。集体询理实施的关键在于多样化的引出，这就需要教师对学生进行“抱持性评价”。寻理数学的展开，需要安全的学习氛围：理解学生寻理中的各种困难，接纳学生的真实，挖掘学生作品的价值，让学生在正向引导里积极主动地融错。

②梯度展示。

学生“正确的‘再创造’总是唯一的，不正确的‘再创造’又是各不相同的，而这些并不完美的‘再创造’恰恰是课堂的重要资源”[1]。梯度展示，是把学生的“再创造”作品由低到高依次展示，在展示中看见自己，在展示中思维扶助。例如图3中，可以清晰地看到学生的思维梯度：单点结构，即直接运用前一次概括的经验，用文字“几”或字母概括地表达不同的数，只见概括不见变化（上面一行左1、2）；多点结构，即用不同的字母概括表达不同的数，看见变化但看不见关系（上面一行左3）；关联结构，即看见变化也看见关系（下面一行）。

梯度展示，可以让学生在对比中询理而进，在对比中自悟。“主动参与和错误反馈会使学习效果最大化”。空框期待，让每一个学生都能主动参与；梯度展示，让每个层面的学生都能在作品的逐层品读中得到适己的错误反馈，相逢适切的思维脚手架。“空框期待”“梯度展示”构成学习过程中的黄金搭档。

3.寻理境界的升华策略。

寻理境界的升华，借助学生的循理而为和师生的巡理而构抵达。

（1）循理而为。

循理而为可以在“前瞻后顾”“左顾右盼”两个维度上展开。

前瞻后顾——新旧知识对比、联系、沟通、整合。比如“用字母表示数”一课，通过回顾低年级时遇到过的“扑克牌中的字母”“算式中的‘字母’”，补充字母兼具表示“特定的数”“未知的数”之意；再通过数学史中字母表示数意义的变迁，使其各类意义结构化，凸显字母表示“一类数”的价值，深化学生的理解。

左顾右盼——跨越学科边界，用数学的眼光观察现实世界。比如“用字母表示数”的课尾，我以“师生年龄”的话题探查学生对“字母表示数”的理解通透度及运用灵活度。

师：你们今年几岁了？（生：11岁）字母表示数那么多优点，为什么不说你们a岁了？

生：（笑着摇头）不行不行！字母再好，也不能随处都用。

师：如果把你们的年龄看作11岁，老师今年的岁数比你们的3倍还大6，知道老师和你们相差多少岁吗？

生：（齐）28岁。

师：随着时间的推移，你们的年龄会怎样？（生：不断地变大）老师的年龄会怎样？（生：也不断地变大）如果用a表示你们不断变化的年龄，那么老师的年龄可以用哪个式子来表示呢？

（课件出示选项：①a×3+6、②a+28、③以上两种都可以）

（学生用手势表示自己的选择：一部分选①，大部分选③）

师：当a=1岁，你们还在妈妈怀里时，老师多大了？

生：（脱口而出）9岁了。（全场爆笑）

前瞻后顾、左顾右盼，学生的寻理在学科关联里拓展、在实践应用里通透。

（2）巡理而构。

心理学研究表明：间隔学习比集中学习更有效[4]。课堂中，经历一段时间的学习后，需要引领学生有意识地回望，教师在此基础上做适当的提升、建构。可以“回头再辨”，在不同学习阶段对同一素材进行多次审视，展现学生学科理解的进阶；还可以回顾整理，对多个知识点进行关联、整合、重构，对思维方法、活动经验提取明晰，对今后学习做出猜想拓展，对学生的学习力、自信度赋能。

参考文献：

[1]张霞.用“空框”透视思维暗盒，借“梯度展示”生长知识：例谈“用字母表示数”的教与学[J].小学数学教育，2017（24）.

[2]中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[3]张华.让学生创造着长大[M].北京：教育科学出版社，2022.

[4]斯坦尼斯拉斯·迪昂.精准学习[M].杭州：浙江教育出版社，2023.

（作者单位：江苏南通市通州区教师发展中心）J