斜面问题中动能定理的应用与摩擦力做功的深入分析

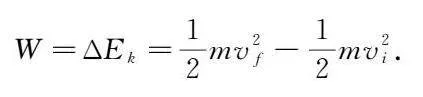
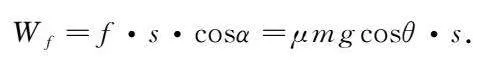
【摘要】斜面问题是经典力学中的常见问题，广泛应用于物理教学与实际工程中.本文结合动能定理与摩擦力做功的原理，深入分析斜面问题中的物体运动情况.通过运用动能定理，探讨了物体在斜面上的加速运动、速度变化及其与位移的关系，同时分析了摩擦力对物体运动的影响.特别是摩擦力的做功过程，通过分析摩擦力的作用，进一步探讨了其对物体动能转化的影响，以期为进一步理解力学问题提供新的视角参考.

【关键词】斜面问题；动能定理；摩擦力；做功分析

1引言

斜面问题是经典力学中的一个重要研究模型，广泛应用于物理学、工程学和日常生活中的各种场景.在斜面问题中，物体沿斜面的运动受到重力、支持力和摩擦力等力的作用，其运动状态和能量转换过程复杂多样.动能定理作为重要的能量守恒定律，能够有效地描述物体在斜面上的运动过程.本文旨在通过动能定理的应用和对摩擦力做功的分析，深入探讨斜面问题中的物理规律和计算思路.

2斜面问题基础

2.1斜面运动基本概念

斜面运动是指物体沿倾斜平面的运动，涉及重力、支持力和摩擦力等力的作用.重力沿斜面分解为平行于斜面的分力和垂直于斜面的分力，前者使物体沿斜面下滑，后者与物体所受斜面的支持力平衡.摩擦力则与物体的运动方向相反，阻碍物体的滑动.

2.2动能定理原理

动能定理是经典力学中的基本原理，描述了物体动能的变化与其所受合外力做的功之间的关系.动能定理的数学表达式为：

W=ΔEk=12mv2f－12mv2i.

其中，W表示合外力对物体做的功，ΔEk表示动能的变化，m是物体的质量，vf和vi分别是物体的末速度和初速度.动能定理在斜面问题中用于分析物体沿斜面运动时的能量转换，通过计算合外力做的功来确定物体的动能变化[1].

3动能定理在斜面问题中的应用

3.1动能定理求解斜面上物体运动问题的方法

动能定理在求解斜面上物体运动问题中具有广泛应用，其步骤如下：第一步，确定物体的初速度vi、末速度vf，以及物体的质量m，以便计算动能变化.第二步，分析物体沿斜面运动时受到的合外力，包括重力沿斜面的分力mgsinθ、支持力N和摩擦力f.其中，摩擦力f可通过 f=μN 得出，μ为摩擦系数，支持力N则为N=mgcosθ.根据动能定理，合外力对物体所做的总功W表示为合外力乘以位移s，即W=（mgsinθ－f）s.此总功W等于动能的增量，表达式为：

W=（mgsinθ－f）s.

其中，s是物体沿斜面的位移，f =μN是摩擦力，μ是摩擦系数，N=mgcosθ是支持力.根据动能定理：

W=ΔEk=12mv2f－12mv2i.

通过上述公式，可以求解物体沿斜面运动的末速度vf 或位移s，从而深入分析物体沿斜面运动时的速度、加速度及能量转换情况.该方法不仅能够求解物体在不同摩擦力条件下的运动，还能揭示能量耗散对物体动能变化的影响.

3.2具体案例分析：斜面上物体的速度与位移关系

假设一质量为m的物体从静止开始沿倾角为θ的粗糙斜面下滑，斜面的摩擦系数为μ.根据动能定理分析其运动情况.初速度vi=0 ，末速度为vf ，位移为s.物体所受重力沿斜面的分力为mgsinθ，摩擦力N=μmgcosθ.根据动能定理，合外力对物体所做的功W等于动能的变化，即：

W=ΔEk=12mv2f－12mv2i.

由于vi=0，得W=12mv2f.同时，W也可以表示为重力沿斜面的分力做功减去摩擦力做功，即W=（mgsinθ－μmgcosθ）s.因此，末速度vf可以表示为：

vf=2（mgsinθ－μmgcosθ）sm.

此公式表明物体速度vf与位移s之间的关系，从中可以分析摩擦力对速度变化的影响[2].

3.3动能定理在斜面问题中的局限性

动能定理在分析斜面问题时具有一定的局限性，这些局限性使得它在某些情况下难以提供全面的解决方案，主要表现在以下几个方面：

（1）动能定理只能描述物体整体的动能变化.动能定理主要用于描述物体整体动能的变化，无法详细分析各个力在不同位置的具体作用效果.这意味着在复杂的斜面问题中，动能定理无法提供关于运动过程中瞬时状态的详细信息.例如，当物体在斜面上滑动时，动能定理可以计算出总的动能变化，但无法精确描述每个瞬间各个力的作用情况.

（1）动能定理未考虑势能变化.动能定理主要关注动能的变化，而忽略了势能的变化.在斜面问题中，物体的高度变化会导致重力势能的变化，这对于全面理解物体的能量转换过程至关重要.动能定理适用于无保守力做功的情况，但在存在摩擦力、弹性力等非保守力的情况下，动能定理的应用就受到了限制.例如，当物体在斜面上滑动时，摩擦力会消耗一部分能量，这部分能量无法通过动能定理直接反映出来.

（2）动能定理主要适用于单一维度的运动.动能定理主要适用于描述沿斜面滑动的单一维度运动，对于多维运动中的转动、滚动等复杂情况，分析力不足.在实际工程和物理问题中，物体的运动往往不仅仅是简单的直线滑动，还可能涉及旋转、滚动等多维度运动.在这种情况下，动能定理无法提供足够的信息来描述这些复杂运动的细节.

（3）动能定理忽略非保守力的影响.动能定理假设系统内的所有力都是保守力，即这些力做的功只与始末位置有关，而与路径无关.然而，在实际问题中，非保守力如摩擦力、空气阻力等的存在会使系统能量发生变化，这些变化无法通过动能定理完全描述.例如，当物体在斜面上滑动时，摩擦力会导致能量的损耗，这部分能量损失需要通过其他方法来计算和分析.

4摩擦力做功的分析方法

在斜面问题中，摩擦力做功的分析可以帮助我们理解能量损耗情况.摩擦力做功的大小与摩擦力的大小、物体的位移以及摩擦力与运动方向的夹角有关.当物体沿斜面运动时，摩擦力f的大小为f =μN，其中μ为摩擦系数，N=μmgcosθ为物体对斜面的正压力，m是物体的质量，g是重力加速度，θ是斜面的倾角.摩擦力对物体做的功Wf可表示为：

Wf=f·s·cosα=μmgcosθ·s.

其中，s为物体沿斜面的位移，α为摩擦力与位移的夹角.通常情况下，摩擦力的方向与物体运动方向相反，因此α=180°，即 cosα=-1.因此，摩擦力做功的公式可以简化为：

Wf=－f·s.

该负值表明摩擦力做功总是减少物体的动能.这个负值表明摩擦力做功总是减少物体的动能[4].通过计算Wf，可以量化摩擦力对动能的消耗程度，进而分析物体的实际运动状态和能量转化过程.

5结语

动能定理和摩擦力做功的分析是解决斜面问题的重要工具.通过本文的研究，可以更深入地理解斜面运动的动力学特性，为工程设计和物理教学提供理论支持.未来的研究可以进一步探索斜面问题中的非线性动力学行为，以及通过动能定理和摩擦力分析对更复杂的力学系统中进行应用，以不断扩展这些理论的应用范围和深度.