不同方法解高中物理多过程问题

【摘要】守恒法和归纳法是求解高中物理多过程多阶段运动问题的常见方法.守恒法常见的有机械能守恒、动量守恒和能量守恒，归纳法关注多过程运动中存在的规律和特点.熟悉和掌握两种解题方法，有助于提高学生解题效率和准确率.

【关键词】高中物理；多过程运动；解题方法

高考物理通常联系多个知识点考查，故运动过程常常由多个不同阶段组成.求解多过程运动问题可以采取不同方法，如守恒法和归纳法，帮助学生掌握更多方法，从而更高效地解答问题.

1守恒法

守恒法是解决物体多过程运动的常见方法之一，运用守恒法解答问题适用于机械能守恒或动量守恒的物理问题，即整个运动过程中重力势能、弹性势能和动能之间互相转化或者整个过程中系统初始状态动量等于终末状态动量.判断多过程运动问题符合上述情况，可运用守恒法列式求解.

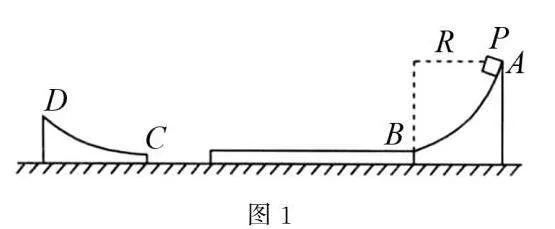
例1如图1所示为某滑雪跳台的一种场地简化模型，右侧是一固定的四分之一的光滑圆弧轨道AB，半径R=1.8m，左侧是一固定的光滑曲面轨道CD，两轨道末端C与B等高，两轨道间有质量M=4kg的薄木板静止于光滑水平地面上，右端紧靠圆弧轨道AB的B侧.薄木板上表面与圆弧面相切于B点.一质量m=2kg的小滑块P（可视为质点）从圆弧轨道最高点A由静止滑下，经B点后滑上木板，重力加速度大小为g=10m/s2，滑块与薄木板之间的动摩擦因素为μ=0.4.

（1）求小滑块P滑到B点时对轨道的压力大小；

（2）若木板只与轨道CD发生一次碰撞，薄木板与轨道CD碰撞为弹性碰撞且碰撞时间极短，运动过程滑块所受摩擦力不变，滑块未与木板分离，求薄木板的运动时间t和最小长度L.

分析在滑块在圆弧轨道和木板上运动的过程中，存在多个运动过程，根据机械能守恒、动量守恒分析碰撞与运动具体情况，得出答案.

解（1）根据题意，小滑块由A到B过程中，由机械能守恒定律有mgR=12mv2B，

在B点，由牛顿第二定律有F－mg=mv2BR，解得F=3mg=60N，vB=2gR=6m/s.

由牛顿第三定律可知，小滑块P滑到B点时对轨道的压力大小为F′=F=60N.

（2）设木板与轨道第一次碰撞瞬间，滑块速度为v1，木板速度为v2，在滑块滑上木板到木板第一次与轨道CD碰撞前的过程中，由动量守恒定律有mvB=mv1+Mv2，由于木板只与轨道CD发生一次碰撞，则由mv1=Mv2，解得v1=3m/s，v2=1.5m/s，

整个过程中木板所受摩擦力不变，滑块滑上木板后，小滑块做匀减速直线运动，由牛顿第二定律可得μmg=ma，解得a=4m/s2.

设从滑块上木板到木板与轨道CD第一次碰撞的时间为t1，则有v1=vB－at1，解得t1=0.75s，由于无能量损失，则木板与轨道CD碰撞后原速率返回做匀减速运动，由对称性可知，木板运动到B端时，速度恰好为0，小滑块的速度为0，运动时间t2=t1=0.75s，则木板的运动时间为t=t1+t2=1.5s.

由上述分析可知，当薄木板返回B端时，小滑块停在薄木板左端，小滑块的位移即薄木板的最小长度，由于小滑块一直做匀减速运动，则有L=v2B2a=4.5m.

2归纳法

归纳法一般用来解决多次碰撞问题，可以是两个物体或物体与挡板之间发生碰撞多次碰撞，也可以是多个物体之间发生的连续碰撞.该方法主要体现在根据多次碰撞运动特点和数据，得到碰撞过程中对应规律或结果，通过计算碰撞的次数得到全过程的数据.归纳法的运用，帮助学生找到重复运动的规律和特点，从而解决问题.

例2某小组设计了一种实验装置，用来研究碰撞问题，其模型如图2所示，光滑轨道中间部分水平，右侧为位于竖直平面内半径R=1.28m的半圆，且半圆在最低点与水平部分相切.5个大小相同的小球并列静置于水平部分，相邻球间有微小间隔，从左到右球的编号依次为0、1、2、3、4，且每个球质量与其相邻左边球质量之比皆为k.将0号球向左拉至左侧轨道距水平部分高h=0.2m处，然后由静止释放，使其与1号球相碰，1号球再与2号球相碰……，所有碰撞皆为弹性碰撞，且碰撞时间忽略不计，不计空气阻力，小球可视为质点，重力加速度为g，下列说法正确的是（）

（A）若k=1，释放0号球后，看到5个（0－4号）小球一起向右运动.

（B）若k=1，释放0号球后，看到只有4号球向右运动.

（C）若k＜1，要使4号球碰撞后能过右侧轨道的最高点，则k应满足0＜k≤2－1.

（D）若k＜1，要使4号球碰撞后能过右侧轨道的最高点，则k应满足0＜k≤3－1.

分析分两种情况分析小球做圆周运动、平抛运动后连续碰撞问题，即小球质量均相等和小球质量不等的情况，分析每一次碰撞过程中机械能和动能的转化情况，可以归纳出碰撞后小球的运动特点，继而选出正确选项.

解当k=1时，小球质量均相等，所有碰撞为弹性碰撞，对0、1号球碰撞过程分析，有mv0=mv′01+kmv11，12mv20=12mv′201+12kmv211，解得v′01=0，v11=v0.同理可知所有碰撞结束后，0、1、2、3号速度均为0，4号球速度为v0，故选项（A）错误，选项（B）正确.

当k＜1时，由机械能守恒定律，可知第0号球与第1号球碰撞前，0号球速度v0=2gh，第0号球与第1号球碰撞过程中动量守恒，机械能守恒，则有mv0=mv′0+kmv1，12mv20=12mv′20+12kmv21，可知碰撞后速度v1=21+kv0，同理可得第1号球与第2号球碰撞后，2号球速度v2=21+k2v0，……，则4号球碰撞后速度为v4=21+k4v0，要使4号球能够通过右侧圆轨最高点，则有12k4mv24=k4mg·2R+12k4mv2，4号球速度的临界值为v≥gR，联立解得21+k8≥16，可得k≤2－1，故选项（C）正确，（D）错误.

3结语

用不同方法求解多过程多阶段的物体运动问题，需要结合具体题意采用合适的方法.其中多次碰撞问题可以用归纳法找到其中规律，守恒法则适合一些合外力为零的系统多阶段运动问题.每种方法的运用特点，都是需要掌握的学习内容.

参考文献：

[1]陈丁丁.高中物理速度分解问题的探究[J].数理化解题研究，2022（06）：86-88.

[2]胡德军.高中物理运动模型的应用[C]//湖北省物理学会，武汉物理学会学术年会.湖北省物理学会;武汉物理学会，2015.