等效法在高中物理解题中的应用

【摘要】物理是一门较为抽象的学科.在求解物理问题时，需要借助一些科学思想，帮助学生顺利突破难题.高中阶段物理解题过程中最常见的一种方法就是等效法.通过等效法可以将复杂的物理问题转化为简单、直观或易于处理的问题，从而简化解题过程.本文以具体题目为例谈等效法在高中物理解题中的应用，希望能给读者带来启示.

【关键词】等效法；高中物理；解题技巧

等效法的实质就是指根据物理现象或过程的等价性，从而将复杂的物理学问题转化为简单、直观、易于处理的问题，以此简化物理解题过程.它的基本思想是通过比较不同物理现象或过程的等价性，找到它们之间的共同点或相似点，从而根据已知的物理学规律求解物理问题.等效法在物理学的各个领域都有广泛应用，如力学、电磁学、光学、热学等.它可以用于解决不同类型的物理问题，包括计算题、实验题等.在具体应用过程中，等效法可以通过类比等效变化、模型化等方式实现，可以以此出发，快速找到解题的突破口.本文将结合具体的物理学问题，详细分析等效法在高中物理解题过程中的应用.

1力的等效法

利用力的等效法解题即是要寻找题目当中的等效力.这一解题方法常用于分析复杂的受力情况，在实验题型中出现的频次较高.在判断等效力时，应从力的三要素上考虑.当两力在作用效果上相同时，才能认为这两力是等效的.在分析物体受力情况时，如果能够引入一个等效力，则问题可以被大大简化.

例1（1）在“探究力的平行四边形定则”的实验中，采用的科学方法是（）

（A）控制变量法. （B）等效替代法.

（C）理想实验法. （D）建立物理模型法.

（2）如图1所示是甲、乙两名同学在做“探究力的平行四边形定则”的实验时得到的结果.若用F表示两个分力F1，F2的合力，用F′表示F1，F2的等效力，则以下哪一个实验结果是可能发生的（）

解（1）平行四边形法则探索的是两个共点力的合成，合力与分力的效果相同，所以此实验采用的是等效性，（A）（C）（D）错误，（B）正确.

（2）两个力的合力理论值应该是平行四边形的对角线，实际值应该是沿着AO的延长线，所以（A）符合实际，故（A）正确，（B）错误.

小结本题为等效法在力学中的应用.在求解本题时，需要根据题目所给实验的探究过程分析问题，将原有的分力问题转变为合力问题，并以此探究力的平行四边形定则.此实验也是高中物理探究力的性质中的关键实验，需要学生重点掌握.

2电源的等效法

电源的等效法即等效电源法.它对于解决电路的动态分析问题以及求变值电阻的最大功率问题十分有效.所谓等效电源法，指的就是对于闭合电路中的定值电阻，有时可以将其等效至电源内部，从而形成一个新的等效电源.在此基础上对新的电路进行分析，从而简化问题[1].

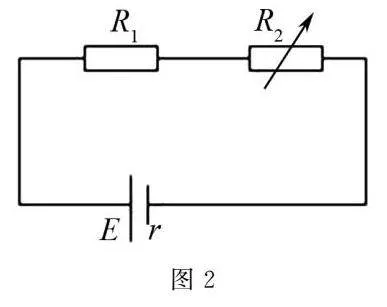
例2如图2所示，R1为定值电阻，R2为可变电阻，E为电源电动势，r为电源内阻，则以下说法中正确的是（）

（A）当R2=R1+r时，R2功率最大.

（B）当R1=R2+r时，R1功率最大.

（C）当R2=0时，R1功率最大.

（D）当R2=0时，电源的总功率最大.

解利用等效法，将定值电阻R1和电源等效为新的电源，这一新电源的内阻为R1+r，则根据电源内阻和外部电阻相等时，电源的输出功率最大得：当R2=R1+r时，电源的输出功率最大，即R2的功率最大，（A）项正确；根据P=I2R1，当流过R1的电流最大时，R1消耗的电功率最大，即当R2=0时，R1功率最大，（B）错误，（C）正确；当R2=R1+r时，电源的总功率最大，（D）项错误，故选（A）（C）.

小结对于R2的功率的分析是本题的难点，在解决此类问题时，通常的解题思路都是把定值电阻和电源看成一个整体，利用等效电源的方法来分析电源的输出功率的变化情况，也就是R2的功率情况.这一思路可以大大简化题目当中的计算量，而且能帮助学生更快速地得到正确的解题结果.

3单摆的等效法

所谓单摆的等效法，即是利用等效法解决单摆的运动或周期问题，这也是高考物理中的常见题型.单摆是现实摆的一种抽象模型，也是一种理想状态下的物理模型.单摆的运动具有周期性，而且它的周期只和摆长与重力加速度相关[2].通常，单摆的摆长长度和周期大小成正相关，重力加速度的大小和周期大小成反相关.因此，在研究单摆振动问题时，可以将摆长或重力加速度等效，以此求解单摆问题.

例3如下图3所示，三根细线于O点相交，试将A、B两端固定在同一水平面上，且两点相距为L，保证AOB为直角三角形，且∠BAO=30°.已知OC线长是L，下端C点系着一个小球（可将小球视作质点），则下列说法中正确的是（）

（A）小球在纸面内摆动，周期为T=2πLg.

（B）小球在垂直纸面方向摆动，周期为T=2π3L2g.

（C）小球在纸面内摆动，周期为T=2π3L2g.

（D）小球在垂直纸面内摆动，周期为T=2πLg.

解小球在纸面内摆动时，圆心是O，摆长为L，故周期为T=2πLg，（A）正确，（C）错误；当小球在垂直纸面方向摆动时，圆心在O点正上方，摆长为L′=（1+34）L，

故周期为T=2π（1+34）Lg，故（B）（D）错误.

小结本题主要考查单摆的周期问题.解题的关键在于根据等效法找到摆长，然后利用单摆的周期公式列式求解.在求解时，学生要根据等效法结合几何关系式，快速找到摆长，以此求解.

4结语

本文通过分析力学板块、电学板块和运动学板块的典型问题，对等效法在高中物理解题过程中的应用进行了应用分析.通过等效法，可以将复杂问题简单化、具体化，起到降低题目难度的作用，为物理解题带来帮助和参考意义.

参考文献：

[1]陈笃杰，唐王雅斌.用“两种等效法”解高考中的理想变压器问题[J].数理化解题研究，2023（10）：138-140.

[2]徐石.利用等效法解答单摆的周期问题[J].高中数理化，2023（02）：31-32.