转换法在高中物理解题中的应用

【摘要】高中物理主要研究自然界中的各种现象，包括声、光、力、电等.在学习过程中，学生对如“力的作用”等抽象概念理解存在一定难度.此时，可使用转换法将抽象问题转换为具体问题，从而达到快速解题的目的.本文提出转换思维方式、转换研究对象两种解题技巧，以期帮助学生实现快速准确解题.

【关键词】高中物理；转换法；解题技巧

在解题过程中，若按正常解法求解有难度时，可以利用转换法，将不可见、不易见的现象转换成可见、易见的现象，将陌生、复杂的问题转换成熟悉、简单的问题，将难以直接测量的物理量通过容易测量的物理量来间接测量.

1转换思维方式解“力的作用”

在解决与“力的作用”相关的问题时，转换思维方式是一种非常有效的策略.其要求学生从不同的角度审视问题，利用逆向思维、等效替代或其他非传统的方法，理解和分析力的作用[1].

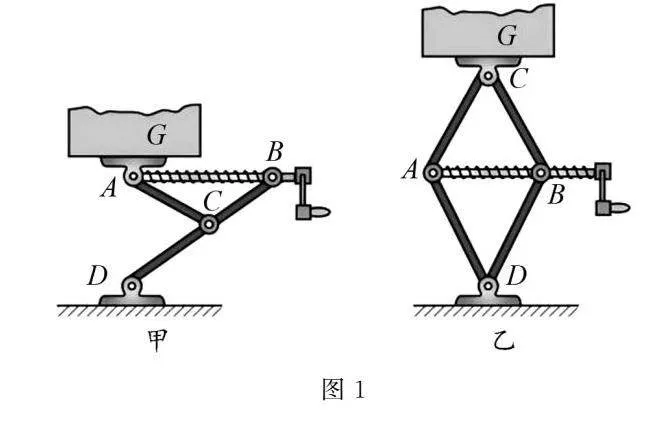
例1如图1所示为汽车内常备的两种千斤顶的原理图，其中甲为Y形，乙为菱形，工作过程中，顺时针转动手柄，通过螺杆作用，AB两点距离缩小，从而达到顶起重物G的目的.反之，逆时针转动手柄，则会实现降低重物G的目的.若将重物G看作汽车，则能够实现顶起车身，更换轮胎的目标.若此时汽车重为G，AC与AB之间的夹角为θ，则螺杆AB的拉力为多少？

解析根据题意分析，重物G与千斤顶间保持相对静止，达到二力平衡状态.若设想螺杆AB突发失效，平衡将被打破，重物G将不可避免地受到重力主导，开始自由下落.此情景清晰揭示了螺杆AB所施加的拉力在维持整个系统稳定与重物G位置不变中扮演着至关重要的角色，即它是实现物体平衡、防止重物下落的关键作用力.

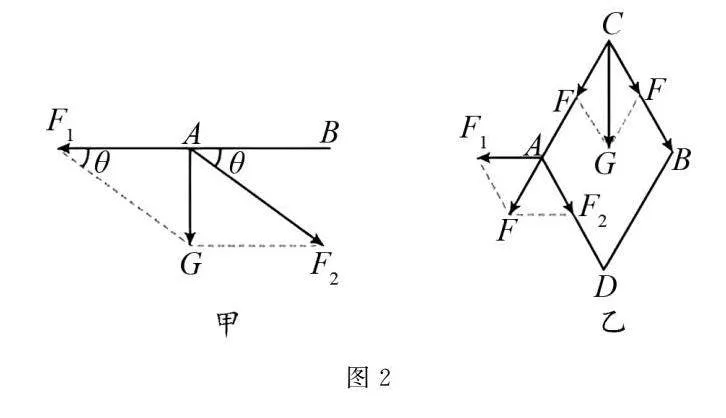
Y形千斤顶的简化模型如图2（甲）所示，可以将重物对A点的垂直压力G，通过力的分解原理，转化为两个分力：一是沿螺杆方向的力F1，二是沿斜杆方向的力F2.两个力与G共同构成一个平行四边形.从图中可以看出，F1和F作为G的分力，其合力与G等大反向，所以F1=Gcotθ.

对菱形千斤顶，根据力的实际作用效果，确定分力的方向，对力G进行二次分解，如图2（乙）所示，G作用在C点，可分解为两个均为F的分力，F作用在A点，又可分解为F1和F2两个分力，其中F1为对螺旋杆的拉力.由于ACBD是一个菱形，根据力的三角形与几何三角形相似可得，在C处可得F=G2sinθ，在A处可得F1=2Fcosθ，所以，F1=G2sinθ·2cosθ=Gcotθ，即Y形和菱形千斤顶螺旋杆AB的拉力均为Gcotθ.

2转换研究对象解“力的作用”

在求解物理问题时，当存在两个或两个以上的物体时，首先要考虑的是研究对象问题.研究对象的正确选取，关系到解题过程的简单与繁琐，关系到解题的成败，若选错了研究对象，有时会出现根本无法求解的现象．但如果能转换思维，合理改变研究对象，问题也就能得到顺利解决.

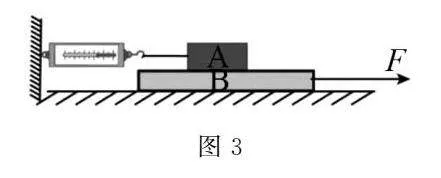
例2如图3所示，A、B为重叠的两木块，木块B在拉力F=6N的作用下，向右做匀速直线运动，此时连接木块A的弹簧测力计示数为2N.则此时木块A对木块B的摩擦力大小为，地面对木块B的摩擦力大小为.

解析本题考查的是对物体间相互作用力及摩擦力的应用.题干描述了A、B两木块在特定条件下的运动状态及受力情况，要求分析两个关键摩擦力：木块A对木块B的摩擦力，以及地面对木块B的摩擦力.若逐个进行受力分析，则计算量较大.此时可以适当转换研究对象，达到快速解题的目的.

木块A在弹簧测力计的拉力和B对A的摩擦力的作用下保持静止状态，两个力是一对平衡力，大小相等.此时弹簧测力计示数是2N，由此可知木块B对木板A的摩擦力为2N；木块A对木板B的摩擦力与木块B对木板A的摩擦力是一对相互作用力，大小相等，所以，木块A对木板B的摩擦力为2N.

在分析地面对木块B的摩擦力时，则以木块B为主要研究对象，进行受力分析，木板B在水平方向上受到拉力F和木块A对木板B的摩擦力以及地面对木板B的摩擦力，其中拉力F水平向右，木块A对木板B的摩擦力fA水平向左，木块B向右做匀速直线运动，所以地面对木块B的摩擦力f地水平向左，则根据二力平衡，则有fA+f地=F.

因为fA=2N，F=6N，所以f地=F－fA=6N－2N=4N.

3结语

综上所述，转换法在高中物理解题中，尤其在处理“力的作用”问题时，展现出独特的优势，其要求学生不拘泥于传统思路，勇于探索新的视角、方法.通过转换思维方式和研究对象，学生能够将复杂、抽象的问题转化为直观、易解的形式，有效提升解题效率和准确性[2].掌握并灵活运用转换法，不仅能够培养学生的物理思维能力和创新能力，还能促进学生对物理概念及原理的深入理解，为后续的物理学习打下坚实的基础.

参考文献：

[1]高世明.转换法在高中物理解题中的应用——以力的作用为例[J].数理化解题研究，2023（13）：128-130.

[2]曾令波.转换法在高中物理解题中的应用[J].数理天地（高中版），2024（08）：45-46.