带电粒子在电场中运动问题的解题策略探究

【摘要】本文探讨在高中物理解决带电粒子在电场中运动问题的几种有效策略，包括利用运动分解法处理曲线运动问题、用功能关系法分析电场力做功的特点，以及用极限思想探讨临界状态等.在解带电粒子在电场中运动问题时，教师应引导学生综合运用物理知识进行分析探究，关注学生在解题过程中的思维方式，帮助其形成科学的思维习惯，从而提高学生的解题能力.

【关键词】带电粒子；电场；解题策略

1引言

带电粒子在电场中的运动是高中物理电磁学部分的重要内容，涉及电场力、电势能等基本概念和规律的综合应用.学生在解决此类问题时常常遇到困难，原因在于问题情境的多样性和物理学科知识的综合性.因此，总结带电粒子在电场中运动问题的解题策略可以帮助学生提高分析问题和解决问题的能力.

2用运动分解的思想处理带电粒子的曲线运动.

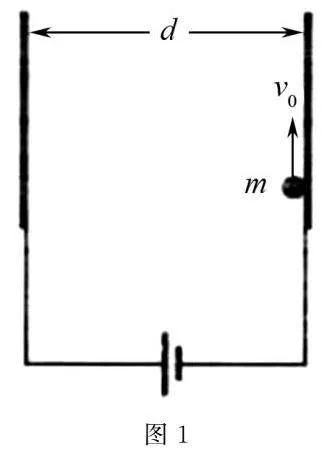
例1如图1所示，一个质量为m、电荷量q的带负电小球在平行板电容器右板内侧竖直向上抛出.电容器两板间距为d，施加电压U.小球最终落在电容器左侧板的同一高度位置.求小球运动过程中到达的最大高度H以及初始抛出速度v0.

解析小球受重力和电场力的作用分别在竖直方向和水平方向做竖直上抛运动及初速度为零的匀加速直线运动，对两个方向的运动分别根据运动学公式列式求解.

对于水平分运动，有d=12at2.

由牛顿第二定律有a=qUmd.

联立解得t=2md2qU.

对于竖直方向分运动，有H=12gt22，

0=v0－gt2.

解得v0=gdm2qU，H=mgd24qU.

本题用到运动分解的思想，将小球的运动分解为竖直方向和水平方向.在处理带电粒子在匀强电场或电场与重力场组成的复合场中做曲线运动时，一般将比较复杂的曲线运动分解为沿电场方向和垂直于电场方向的两个分运动求解.

3用功能关系法处理相关问题

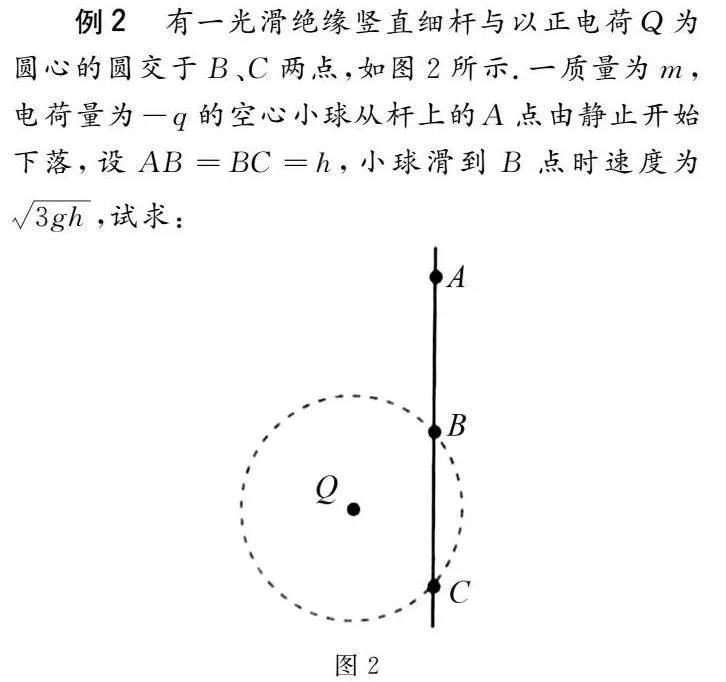
例2有一光滑绝缘竖直细杆与以正电荷Q为圆心的圆交于B、C两点，如图2所示.一质量为m，电荷量为-q的空心小球从杆上的A点由静止开始下落，设AB=BC=h，小球滑到B点时速度为3gh，试求：

（1）小球滑至C点的速度；

（2）A、B两点的电势差.

解析（1）因B、C是在电荷Q产生的电场中处在同一等势面上的两点，即UBC=0，所以从B到C时电场对带电小球所做的功为零.

由B→C，根据动能定理，

得mgh=12mv2C－12mv2B.

将vB=3gh带入，得vC=5gh.

（2）由A→B，根据动能定理mgh+（－qUAB）=12mv2B.

故UAB=－mgh2q.

本题用到功能关系法.电场力做功只由始末位置的电势差决定，与电荷经过的路径无关，即WAB=qUAB，因此在处理粒子在均匀强电场或非均匀强电场中进行直线运动或曲线运动相关问题时，采用功能关系法都是一种行之有效的解题方法.

4用极限思想分析临界问题

例3如图3所示，一束电子流经U=5000 V加速电压加速后，在距两极板等距离处垂直进入平行板间的匀强电场，若两板间距d=1.0 cm，板长l=5.0 cm.问：要使电子能从平行板间飞出，两个极板上能加的最大电压是多少？

解析求解带电粒子在电场中运动的临界问题时，关键是找到临界状态所对应的临界条件，而临界条件可以借助极限法进行分析.

①根据动能定理可得，电子在加速过程中有eU=12mv20，

②电子进入偏转电场后可得l=v0t，

③进入偏转电场后电子垂直于版面的加速度为a=Fm=eU′dm，

④偏距为y=12at2，

⑤当偏距y≤d2时，电子能从平行板间飞出.

联立①～⑤可得

U′≤2Ud2l2=2×5000×1.0×10－225.0×10－22V=400V.

故要使电子能从板间飞出，所加电压最大为400V.

本题用到极限思想，在给定的加速电压下，偏转电压U′对电子在平行板间的偏转距离有决定性影响.U′越大，电子的偏距就越大.当U′增大到一定值时，电子将恰好沿着极板边缘飞出.这个临界偏转电压就是题目所求的最大电压.

5结语

解决带电粒子在电场中运动问题需要综合运用物理学科知识，灵活采取恰当的解题策略.其中，运动分解法、功能关系法和极限思想等，都是行之有效的方法.在教学实践中，教师还应注重引导学生利用所学物理知识综合分析问题的特点，进而选择合适的解题策略.同时，要关注学生解题过程中的思维方式，适时给予引导，帮助学生梳理思路，培养科学的思维习惯.

参考文献：

[1]曹莉.探讨带电粒子在电、磁场中的运动[J].数理化解题研究，2024（25）：94-96.

[2]蒋金团，代朝荣.例析带电粒子在圆形磁场中做圆周运动[J].数理化学习（高中版），2024（07）：50-53.

[3]余胜强.带电粒子在电、磁场中的运动分析[J].高中数理化，2023（24）：13-14.

[4]陈丰波.学好电场“三条线”，解题变得不再难[J].高中数理化，2023（Z2）：40-41.