“五定”定乾坤

【摘要】带电粒子在磁场中的运动是高中的重难点内容，学生在找圆心、做轨迹、找半径、找圆心角以及求时间问题上困难重重.本文从构建情境、“五定剖析”及典型例题方面深入浅出地进行分析，希望给学生在这块内容的学习上提供参考.

【关键词】磁场；圆周运动；高中物理

带电粒子在磁场中的运动经常出现在高考压轴计算题中，是学生学习的难点.突破这类问题的关键是学会做粒子运动轨迹，并巧妙构建几何关系，利用题中的长度和角度求解轨迹半径，同时需要知道速度偏转角、圆心角、弦切角之间的关系，这样可以提高解题效率，达到事半功倍的效果.

1构建情境——提供铺垫

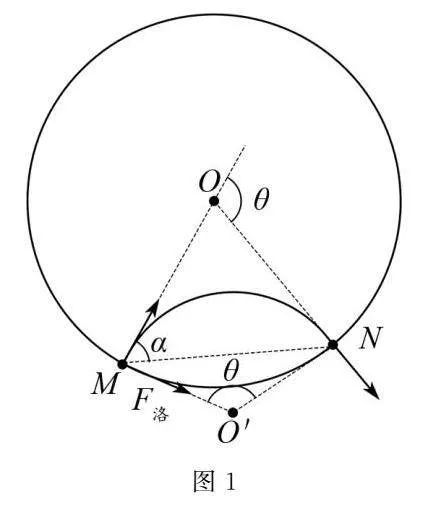
如图1所示，有一垂直纸面向里，半径为R的圆形磁场，磁感应强度为B，有一带电量为－q，质量为m的粒子从M点正对圆形磁场的圆心射入，经磁场偏转后从N点背离圆心射出，粒子进出磁场的速度的偏转角为θ，弦切角为α，不计粒子的重力.

2方法介绍——“五定剖析”

一定轨迹据左手定则可得带电粒子的轨迹，如图1所示.

二定圆心作入射速度和出射速度的垂线相交于O′点，则O′点为粒子在圆形磁场中做圆周运动的圆心；或作入射速度的垂线及入射点和出射点的连线的中垂线的交点O′，O′点即为粒子在圆形磁场中做圆周运动的圆心.

说明根据需要合理选择带电粒子在磁场中的运动轨迹和轨迹的圆心的确定顺序，先确定圆心，再确定轨迹更方便处理问题.

三定“圆心角”速度的偏转角等于圆心角，圆心角为弦切角的2倍，即θ=2α.在实际应用中，在“四定半径”中如果用三角函数解直角三角形需要先求出圆心角，如果不用三角函数解直角三角形，而是用勾股定理解直角三角形时往往不需要先求圆心角.

四定半径方法1公式法

带电粒子在磁场中受到的洛伦兹力提供粒子做圆周运动的向心力，则qvB=mv2r，所以r=mvqB.

方法2数学法

（1）利用三角函数求解：若能找到一个直角三角形的一个已知角（非直角）及一条边长，可根据三角函数知识求带电粒子在磁场中运动的轨道半径r.在图1中的直角三角形OMO′中，∠MO′O=θ2，MO=R，所以轨道半径为r=Rcotθ2.

（2）利用勾股定理求解：若能找到一个直角三角形，但无已知角，往往可利用勾股定理建立方程求带电粒子在磁场中运动的半径；通常公式法和几何法在同一题目中需同时使用，利用两种方法求出的半径r建立方程，再求其他物理量.

五定时间方法1

t=θ2πTT=2πmqB，带电粒子在磁场中的运动时间t和粒子在磁场中运动的速率v的大小无关.此方法除了求带电粒子在磁场中运动的时间t，通常还在比较不同速率v的粒子在同一磁场中运动的时间长短问题时使用.

方法2

t=sv，s为带电粒子在磁场中运动通过的弧长，若带电粒子速率v相同，粒子在磁场中通过不同的弧长s，则所用时间t不同.此方法除了求带电粒子在磁场中运动的时间t，还在处理带电粒子在磁场中运动的时间极值时使用.例如，在某一平面内速度大小相等的粒子在某一圆形磁场中运动时，圆形磁场的直径对应的粒子的轨迹所用时间最长；在同一平面内从同一点向各个方向发出的速度大小相等的能到达同一条直线的粒子中，发射点到直线的垂线段对应的轨迹所用时间最短.

3“五定”定乾坤—例题精析

例题如图2所示，一个质量为m、电荷量为q、不计重力的带电粒子从x轴上的P点以速度v沿与x轴正方向成60°的方向射入第一象限内的匀强磁场中，并恰好垂直于y轴从Q点射出第一象限.已知OQ=a，则（）

（A）粒子带正电.

（B）粒子运动的轨道半径为233a.

（C）匀强磁场的磁感应强度为B=3mv2qa.

（D）粒子在第一象限中运动的时间为t=43πa9v.

详解一定轨迹根据左手定则可知，该粒子带负电，故（A）错误.

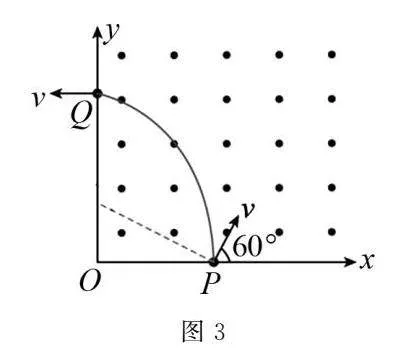
二定圆心做出粒子在磁场中的运动轨迹如图3所示.

三定半径由几何关系可得R+Rcos60°=a，解得R=23a，故（B）错误.

根据洛伦兹力充当向心力有Bqv=mv2R，解得B=3mv2qa，故（C）正确.

四定圆心角根据几何关系可知粒子在磁场中转过的圆心角为2π3，而粒子做圆周运动的周期T=2πRv，将R=mvqB代入可得T=2πmqB.

五定时间由此可得粒子在第一象限内运动的时t=13T=13×2πmqB=2πm3q×2qa3mv=4πa9v，故（D）错误.

故选（C）.

点评根据题中两个速度方向确定两个洛伦兹力方向，两个洛伦兹力交点即为圆心，进而确定运动轨迹以及圆心角.“五定”是处理带电粒子在磁场中运动的一般过程，在实际应用中需根据实际需要合理选择“五定”的使用顺序.

4结语

带电粒子在磁场中的运动对学生综合能力要求较高，需要综合应用物理、数学知识解决问题，需要学生根据题中条件确定运动轨迹，进而找出圆心、半径、圆心角以及运动时间.利用几何关系求解半径时，要注重培养信息分析能力和作图能力，可以根据提取题目中的关键条件求解，提高处理复杂问题的能力，更好适应新高考的要求.