微元法在高中物理解题中的应用探讨

【摘要】微元法作为高中物理中的重难点知识，在解题中有着广泛应用.微元法可以将复杂的题目分割成若干简单的小问题，帮助学生逐步攻克难题.本文通过典型例题，详细说明微元法在高中物理解题中的应用，以供读者参考.

【关键词】微元法；高中物理；解题；应用

微元法通过对研究内容或过程进行无穷小的分割，将整体中的复杂部分简化为单个简明的片段，从而让学生能够从微观角度洞察物理的变化，并最终理解整体的规律.该方法不仅促进了学生对物理知识的掌握，同时显著增强了他们的问题解决能力.

1在运动学中的应用

例1根据图像回答下列问题：

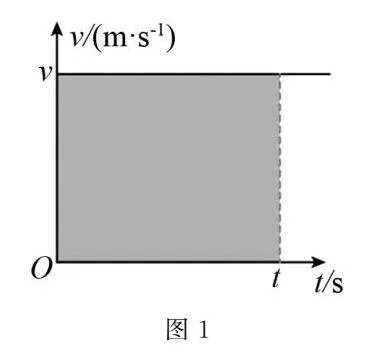
（1）以速度v做匀速直线运动的物体，时间t内的位移是什么？在图1所示的图像中可以用什么来表示？

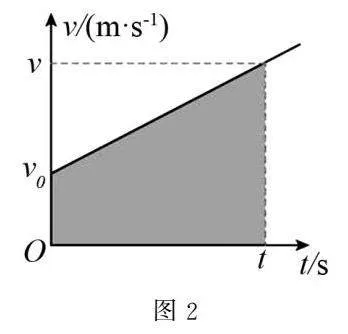
（2）图2是匀变速直线运动的v-t图像，根据（1）的结论，试猜想：匀变速直线运动的位移在图2中可以用什么来表示？

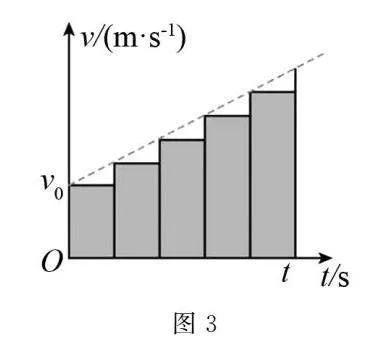
（3）如图3，将图2的运动分割成几小段，因每段很短，可认为在这一小段上物体速度不变.基于此，在图3中，各个小矩形面积的和表示的物理意义是什么？

（4）如图4所示，将图2的运动划分为更多的小段，对比图4和图3，分析（2）的猜想是否正确.

解析（1）物体以速度v做匀速直线运动，设位移为s，则时间t内的位移为s=v·t.在图1的v-t图像可知，横坐标表示时间t，纵坐标表示速度v，由图可知图线围成的面积表示位移.

（2）在图1的v-t图像可知，图线围成的面积表示位移.则可猜想：匀变速直线运动的位移在图2中可以用面积来表示.

（3）若将图2的运动分割成几小段，因每段很短，可认为在这一小段上物体速度不变.因此，每小段上，速度与时间的乘积可近似为物体的位移.各小矩形的面积和近似为全过程中物体的位移.

（4）将运动过程划为更多的小段后，把整个运动过程分割得很细，分割越细.这些小矩形的面积和便可更准确地反映物体的位移.所以（2）的猜想正确.

点评在本问题中，将物体的整个运动过程分割成若干个“微过程”，每个“微过程”可认为速度不变，速度与时间的乘积可近似为物体的位移.那么，各小矩形的面积和近似为全过程中物体的位移.巧妙地运用了微元法处理了这类运动问题.

2在静电场中的应用

例2如图5，圆心为O、半径为R的均匀带电圆环所带电荷量为Q，P为垂直于圆环平面的对称轴上的一点，OP=L，电场力常量为k，求P点处的场强大小.

解析如图6所示，将圆环看成由n个小微元组成，当n足够大时，每个小微元都可看作点电荷，其所带电荷量Q′=Qn，则每个小微元在P点处产生的场强大小均为E=kQnr2=kQnR2+L2.由对称性知，各个小微元在P点处的场强E沿垂直于对称轴方向的分量Ey相互抵消，沿对称轴方向的分量Ex之和即为带电圆环在P点处的场强EP，所以EP=nEx=nkQnR2+L2cosθ=kQLR2+L232.

点评本题中，带电圆环所带的电荷量均匀分布，从圆环上任取一个微元，每个微元可看作点电荷，求出微元在P点的场强后，再运用场强的叠加求解圆环在P点的场强.

3在电磁感应中的应用

例3如图7所示，两平行金属导轨水平放入磁感应强度为B、方向竖直向上的匀强磁场中，导轨间距为L，导轨左端接有一电容为C的平行板电容器.一质量为m的金属棒ab垂直放在导轨上，在水平恒力F的作用下从静止开始运动.棒与导轨接触良好，不计金属棒和导轨的电阻以及金属棒和导轨间的摩擦.求金属棒的加速度并分析金属棒的运动性质.

解析运动过程分析：取一极短时间Δt，棒做加速运动，持续对电容器充电，则存在充电电流，

则F－BIL=ma，I=ΔQΔt，ΔQ=CΔU，ΔU=ΔE=BLΔv，

联立可得F－CB2L2ΔvΔt=ma，

其中a=ΔvΔt，

则可得a=Fm+B2L2C，

加速度恒定，所以棒做匀加速直线运动.

点评在没有明确加速度的变化情况之前，金属棒的运动情况可能比较复杂，如果取运动过程中的极短时间Δt，可认为看认为在这一“过程微元”上电流不变，进而根据电学和力学相关知识进行求解.

4结语

综上所述，微元法在高中物理解题中有着至关重要的地位.它为学生处理复杂物理问题提供了一种巧妙的思路，将不规则、连续变化的物理过程分割成无数个微小的单元，使问题简化且更易理解.掌握微元法，不仅能提高学生解题的效率和准确率，更有助于培养他们的物理思维和科学探究能力.这要求教师在教学过程中重视微元法的讲解和训练，引导学生熟练运用微元法，让学生在面对物理难题时能够灵活使用这一有力工具，为高中物理学习和问题解决奠定坚实的基础.

参考文献：

[1]张家民.微元法在高中物理解题中的应用研究[J].中文科技期刊数据库（引文版）教育科学，2023（3）：4.

[2]雷文胜.例谈微元法在高中物理解题教学中的实践应用[J].高中数理化，2023（S1）：107-108.