生活中常见的圆周运动问题分类剖析

【摘要】高中物理中圆周运动可以根据不同情境和状态总结出各种模型，也有对应的命题特点和解题思路.生活中常见的圆周运动模型主要有三类：转弯模型、拱桥模型、转盘模型，总结问题特点和解题思路，有助于学生更高效地分析问题，解决问题.

【关键词】高中物理；圆周运动；解题技巧

1转弯模型

转弯模型主要有两大考查方向：一是火车转弯做圆周运动，二是圆弧路段汽车做圆周运动.转弯模型的分析与解答，应结合受力分析和向心力的来源求解.

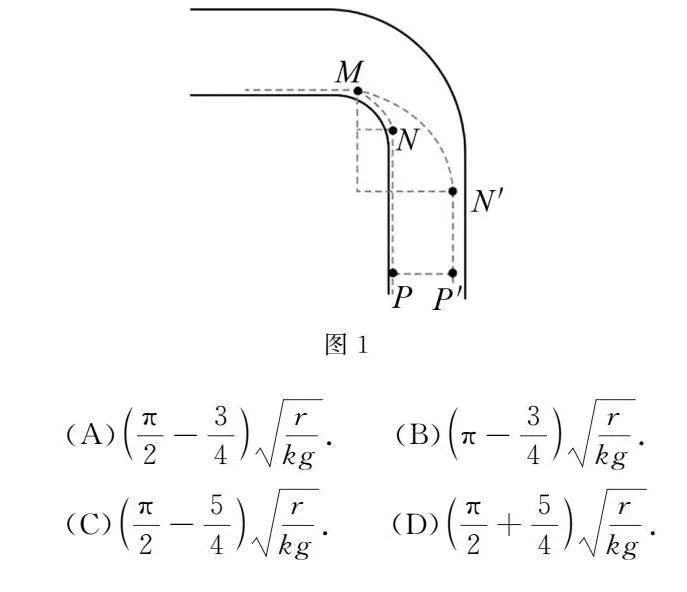
例1如图1所示，MN为半径为r的14圆弧路线，NP为长度为19r的直线路线，MN′为半径为4r的14圆弧路线，N′P′为长度为16r的直线路线.赛车从M点以最大安全速度通过圆弧路段后立即以最大加速度沿直线加速至最大速度vm，并保持vm匀速行驶.已知赛车匀速转弯时径向最大静摩擦力和加速时的最大合外力均为车重的k倍，最大速度vm=6kgr，g为重力加速度，赛车从M点按照路线MNP运动到P点与按照MN′P′路线运动到P′的时间差为（）

（A）π2－34rkg. （B）π－34rkg.

（C）π2－54rkg. （D）π2+54rkg.

分析分别对两种不同轨道MNP和MN′P′进行分析，赛车在轨道上的运动由圆周运动和直线运动组合形成，在圆弧轨道上由外力提供向心力，产生向心加速度，联合不同公式表示运动时间，通过运算求出时间差.

解赛车从M点按照MNP路线运动到P点过程中做匀速圆周运动通过有kmg=mv21MAPsOMgEuiiZB0kL11AlkA==r，

t1=T14=14·2πrv1，

在NP直线路线上做匀加速直线运动，有kmg=ma1，

vm=v1+a1t2，

解得t1=πkgr2kg，t2=5kgrkg，

可知在NP直线路线匀加速至最大速度过程的位移为

x1=v1+vm2t2=17.5r＜19r，

则匀速运动过程的时间为t3=19r－x1vm=kgr4kg；

赛车从M点按照MN′P′路线运动到P′点过程中做匀速圆周运动，有kmg=mv224r，

t4=T24=14·2π·4rv2，

在N′P′直线路线上做匀加速直线运动，有kmg=ma2，

vm=v2+a2t5，

解得t4=πkgrkg，t5=4kgrkg，

可知在N′P′直线路线匀加速至最大速度过程的位移为x2=v2+vm2t5=16r，

匀加速至最大速度时，恰好到达P′，则赛车从M点按照MNP路线运动到P点与按照MN′P′路线运动到P′点的时间差为Δt=t4+t5－t1－t2－t3，

可知Δt=π2－54rkg，正确答案为选项（C）.

2拱桥模型

拱桥模型中，可将拱桥类比成圆周运动的一部分轨道，这类模型的解题思路主要在最高点物体所受重力和桥面对物体的支持力的合力提供向心力.这类模型还可以拓展成竖直平面的凹槽圆弧轨道运动，分析思路都比较相似，需要认真分析与解读.

例2当汽车通过拱桥顶点的速度为v时，车对桥顶的压力为车重的34，如果要使汽车安全通过该拱桥（不脱离地面），则汽车通过桥顶的速度可以为（）

（A）v2. （B）v3. （C）3v. （D）4v.

分析首先分析最高点位置提供向心力的合力组成部分，其次分析汽车做圆周运动临界状态需要提供的合力大小，最后分析安全速度与原速度的关系，可得到答案.

解根据牛顿第三定律，

可得FN=34mg，

根据牛顿第二定律，

可得mg－FN=mv2r，

mg=mv′2r，

解得v′=2v，

汽车速度小于2v时，能安全通过该拱桥（不脱离地面），故正确答案为选项（A）（B）.

3转盘模型

转盘模型中，物体做圆周运动的向心力主要由摩擦力提供，其他特殊情况还需要特别分析.分析和解答转盘模型，应结合角速度ω、向心力合外力F列式求解.

例3如图3所示，在匀速转动的水平圆盘上，沿直径方向放着用轻绳相连可视为质点的物体A和物体B，A的质量为3m，B的质量为m，它们分居圆心两侧，到圆心的距离分别为RA=r，RB=2r，A、B与盘间的动摩擦因数相同，最大静摩擦力等于滑动摩擦力.A、B与圆盘一起绕中轴线匀速转动的最大角速度为ω1；若只将B的质量增加为2m，A、B与圆盘一起绕中轴线匀速转动的最大角速度为ω2.转动过程中轻绳未断，则ω1ω2为.

分析首先分析不同物体在同一水平面上以不同角速度做圆周运动的具体情况，其中向心力由绳子拉力和摩擦力的合力构成，需要列式求解，用变量表示并得到具体答案.

解当A、B与圆盘一起绕中轴线匀速转动达到最大角速度ω1时，

对B：T－μmg=mω21·2r，

对A：T+μ·3mg=3mω21r，

解得ω1=2μgr，

若只将B的质量增加为2m，A、B与圆盘一起绕中轴线匀速转动的最大角速度为ω2时，

对B：T′+μ·2mg=2mω22·2r，

对A：T′－μ·3mg=3mω22r，

解得ω2=5μgr，

所以ω1ω2=25.

4结语

上文列举了3种常见的圆周运动模型，不同模型的特点和对应解题思路都是学生需要掌握的内容.解答圆周运动问题的要点是找到提供向心力的合外力，还需要结合牛顿运动定律、动能定理进行求解.

参考文献：

［1］毛宁，吴峰，惠治鑫，等.基于"圆周运动"模型建构的高中物理深度学习[J].物理通报，2022（08）：63-67+73.

［2］鲍龙.高中物理模型的分类及建模重要性[J].中学生数理化（教与学），2017（04）：20.