感受方法普适性的课堂对话研究

【摘要】在探究数学对象性质的过程中体会探究数学对象的一般方法.探究数学对象的性质，一方面可以更深入认识这个对象，另一方面能更好地解决与其相关的数学与现实问题.教学设计要有意识地关注逻辑连贯，思想一致，方法普适.

【关键词】 高中数学;逻辑推理;课堂教学

教学中要丰富数学内容所蕴含的数学思想和方法，使学生体会研究的内容、过程和方法一脉相承，体悟具有普适性的数学思想和方法，逐步形成数学思维方式，落实数学学科核心素养.本文以选择性必修三“二项式系数的性质”为例，谈一谈想法.

人脑对规律有先天的敏感性，善于发现并总结规律.在组合数的两个性质的基础上，预感a+bn的展开式的二项式系数C0n，C1n，C2n，…，Ckn，…，Cnn有很多值得探究的性质.类比函数性质、数列性质的学习经验，从特殊到一般地对二项式系数进行研究.通过一个个数学对象的探究，让普适性的数学方法根植于学生的潜意识中.

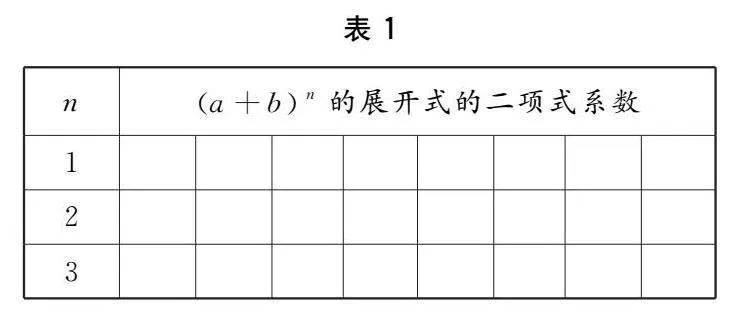
填写表1，观察表格.

问题1通过观察图表的结构，你发现了什么规律？能否与已学过的知识相联系？

学生A通过观察结构，发现其中系数排列具有对称性，增减性.通过运算也可以发现规律.

设计意图学生直观感知代数中研究问题的基本方法，也是数学学习中经常使用的思维方法.

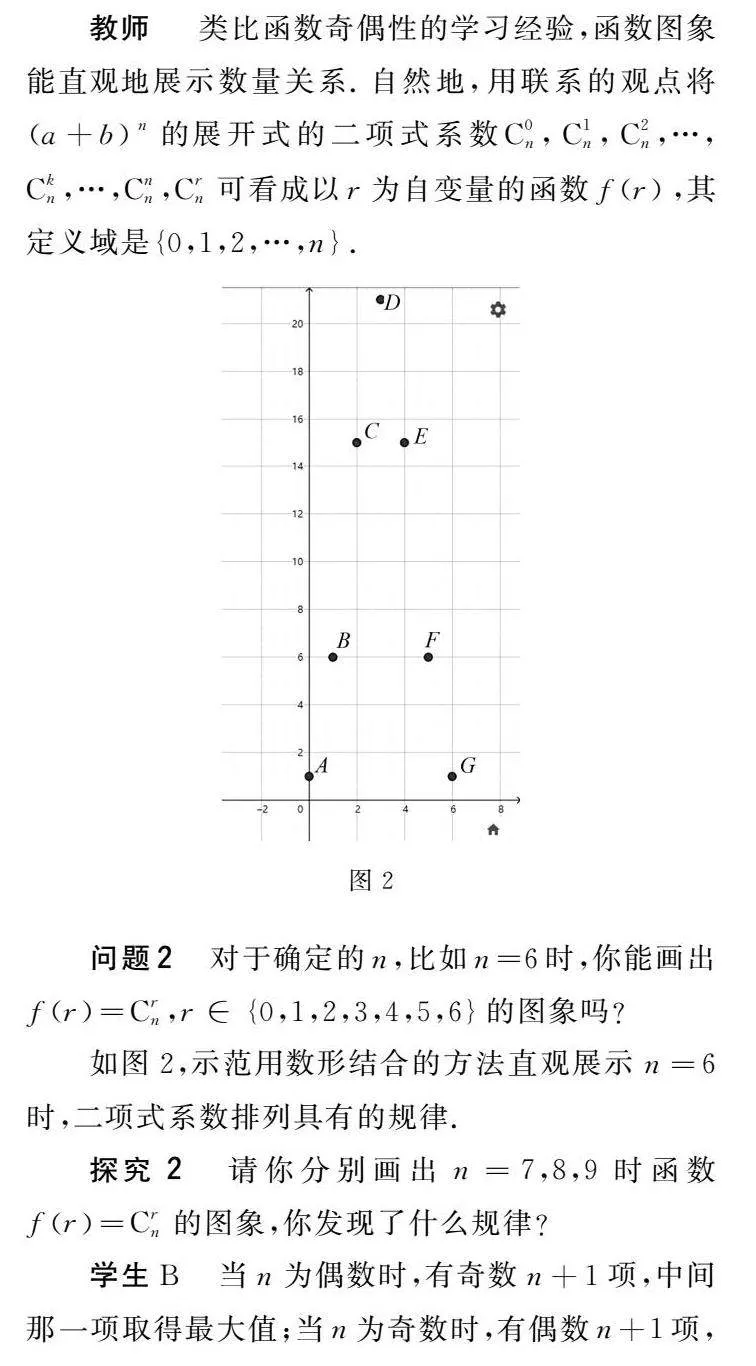
教师类比函数奇偶性的学习经验，函数图象能直观地展示数量关系.自然地，用联系的观点将a+bn的展开式的二项式系数C0n，C1n，C2n，…，Ckn，…，Cnn，Crn可看成以r为自变量的函数fr，其定义域是0，1，2，…，n.

问题2对于确定的n，比如n=6时，你能画出fr=Crn，r∈0，1，2，3，4，5，6的图象吗？

如图2，示范用数形结合的方法直观展示n=6时，二项式系数排列具有的规律.

探究2请你分别画出n=7，8，9时函数fr=Crn的图象，你发现了什么规律？

学生B当n为偶数时，有奇数n+1项，中间那一项取得最大值；当n为奇数时，有偶数n+1项，中间两项相等，且同时取得最大值.

教师结合这些具体例子进行数学表达.

（1）对称性.文字描述：与首末两端“等距离”的两个二项式系数相等.

数学符号语言理论推导：由Cmn=Cn－mn得到.

从n个不同元素中取出m个元素后，剩下（n－m）个元素，即从n个不同元素中取出m个元素的组合数与剩下（n－m）个元素的组合数相等.

图象：直线r=n2将函数fr=Crn的图象分成对称的两部分.

（2）增减性与最大值.

文字描述：函数fr=Crn的图象在直线r=n2的左侧部分，Ckn随k的增加而增大；结合对称性知，在直线r=n2的右侧部分，Ckn随k的增加而减小.

问题3你能证明这一性质吗？

由于组合数Ckn，Ck－1n均为正整数，于是CknCk－1n=nn－1…n－k+1k！nn－1…n－k+2n－k+1k－1！=n－k+1k，当n－k+1k>1时，即k<n+12时，Ckn随k的增加而增大；当k>n+12时，Ckn随k的增加而减小.

当n为偶数时，最中间那一项Cn2n取得最大值；

当n为奇数时，展开式有偶数n+1项，中间两项Cn－12n与Cn+12n相等，且同时取得最大值.

设计意图动手动脑中学生的思维走向所学知识的本质.形成数学思考结构的系统性、普适性.

问题4运算是发现规律的有效途径，算一算图1中每一行数的和，你发现了什么规律？

学生C第n行数的和为2n.

教师按照特殊到一般的研究思路，我们猜想C0n+C1n+C2n+…+Ckn+…+Cnn=2n.

追问由 1+xn=C0n+C1nx+C2nx2+…+Cknxk+…+Cnnxn，你能证明这一性质吗？

可具体化、特殊化，令x=1，得2n=C0n+C1n+C2n+…+Ckn+…+Cnn，即a+bn展开式的各二项式系数和等于2n.

问题5更进一步，算一算图1中每一行数的奇数项的和，以及偶数项的和，你发现了什么规律？

学生D每行奇数项的和等于偶数项的和.

例题求证：在a+bn的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和.

分析奇数项的二项式系数的和为C0n+C2n+C4n+…，

偶数项的二项式系数的和为C1n+C3n+C5n+….

由a+bn=C0nan+C1nan-1b+C2nan-2b2+…+Cnnbn，令a=1，b=－1可证明结论.

进一步追问C0n+C2n+C4n+…=C1n+C3n+C5n+…等于多少？

分析C0n+C2n+C4n+…=C1n+C3n+C5n+…=2n2=2n-1.

设计意图体会发现规律的一般方法，构建研究数学对象的基本路径.感受数学研究对象在变，但研究的思想方法不变.

结语

当学生获得了方法，养成了习惯，就会自发地去探究.研究方法上，应在实际教学过程中加强通过代数运算和图象直观揭示性质的引导和明示.构建从具体到抽象、从特殊到一般的过程，从而归纳概括出精确刻画性质的方法，从而提升素养.让重要的数学概念、思想、方法得到反复理解的机会.

【福建省课题《人工智能赋能中学数学课堂对话质量优化研究》立项批准号Fjxczx23-120】

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020.

[2]章建跃.章建跃数学教育随想录[M].杭州：浙江教育出版社，2017.