立体几何单元复习课

【摘要】本文通过一节案例课的思路分析，将立体几何中的最短距离问题通过划归的方式与平面解析几何联系到一起.学生通过感受动态几何中展开平面、证明全等、还原长度关系、求解线段长度的流程感受到数学中不同模块的联系，深化数形结合的数学思想.

【关键词】立体几何；最短距离；解题技巧

1教学内容分析

立体几何是高中数学的重要章节之一，到此阶段高三学生已经完成了一轮复习，对高中整体内容有了一定的认知.在此节点，借助“最短距离”问题使学生回顾和建构完整的立体几何知识体系，以具体的棱柱、棱锥、旋转体构建点、线、面间位置框架，进行熟练的转化和迁移.

立体几何中的“距离”问题是定量分析空间几何元素（点、线、面）间位置关系的重要几何量.在研究距离问题时，常将空间问题转化为平面问题处理，这是化归思想在立体几何中的具体应用.在求解空间距离的相关问题时，一般包括三个部分：求作、论证和计算，这三部分是不可分割的整体.通过这一章节内容的学习，学生回顾之前与旋转体有关的表面积问题的求解思路，同时也掌握在展开过程中分类讨论的精确性和还原截面的方法.

2学情分析

高三学生在之前的立体几何学习中已经学习了点到面、线到面、线到线、面到面这四种距离问题，其中多以垂直为主，其实这已经初步渗透了“最短距离”的思考模式.在后段的学习过程中，比如圆柱和圆锥的表面积求法中，学生了解了展开的思维.

虽有所涉及，但学生在此阶段刚刚完成立体几何的第一轮学习，因此借助此节课的内容，通过“最短距离”多种问题的变换应用，强化学生“想图、画图、识图、解图”的能力，重视图形语言、文字语言、符号语言相互转化的训练.尤其重视对所画的立体图形、三视图与真实图形思维理解上的一致性.

3教学目标

（1）知识与技能：通过求解最短距离掌握“展开”的立体几何距离问题基本解法.

（2）过程与方法：在展开过程中明确分类讨论的思想以及截面还原精确性的把控，达成实际图形和斜二测图象的统一.

（3）情感态度与价值观：通过最短距离的不同解法培养学生善于分析题意，富于联想，以提高学生的空间想象能力，强化主动探索问题的精神和科学理性的思维方法.

4教学过程

4.1借典引入，提升兴趣

其实早在1903年，就已经有相应的数学谜题开始流传，也就是著名的蜘蛛抓苍蝇的故事.杜登尼（Dudeney，1857—1930）是19世纪英国知名的谜题创作者．“蜘蛛和苍蝇”问题最早出现在1903年的英国报纸上，是杜登尼最有名的谜题之一．它对全世界难题爱好者的挑战，长达四分之三个世纪．

4.2分类讨论思想的渗透

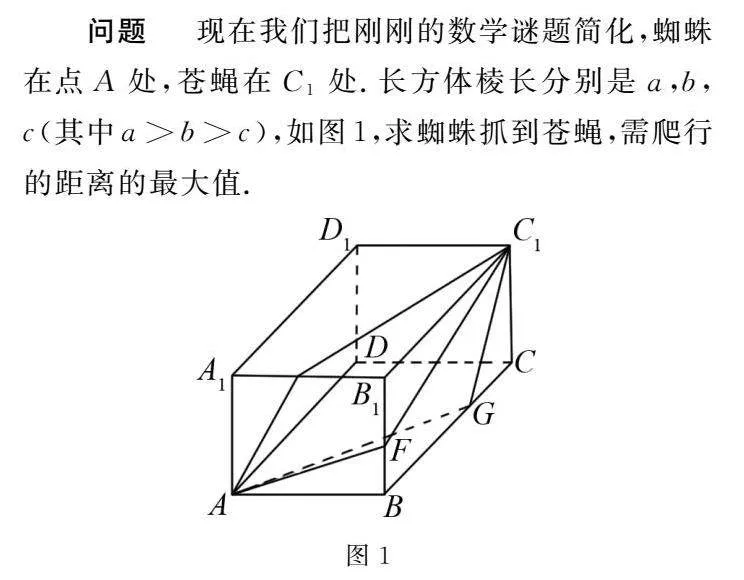
问题现在我们把刚刚的数学谜题简化，蜘蛛在点A处，苍蝇在C1处.长方体棱长分别是a，b，c（其中a＞b＞c），如图1，求蜘蛛抓到苍蝇，需爬行的距离的最大值.

题目分析通过此题提出展开的一大重点——分类讨论.为了和之后的问题产生对应，引导学生从经过棱的角度进行分类.

通过观察，我们可以发现蜘蛛所经过的棱共有6种可能，而其中两两具有对应关系.因此最后归类为如下3种，如图2.

立体问题平面化，将立体几何的距离问题变为求出三个矩形对角线长短进行比较的问题.

4.3截面还原，手脑统一

问题如图3，在直三棱柱ABC-A1B1C1中，底面为直角三角形∠ACB=90°，AC=4，BC=CC1=2，P是BC1上一动点，则CP+PA的最小值是.

题目分析在这道题中，学生不需要像上题一样讨论棱的分类问题，已经确定为BC1，难点设置在了是哪两个面的展开上，由于图象不如上道题完整，所以需要学生自己将截面进行补全，从而回顾立体几何中公理三的推论——直线和直线外一点确定一个平面.

展开后，得到两个三角形BC1A1和三角形BC1C，为了确定截面的具体形状，从而算出每个三角形的三条边长，明确特殊的角度，从斜二测画法中还原为实际图象后，再通过平面几何求出线段距离.

4.4二维与三维的类比

问题如图4，正方体ABCD-A1B1C1D1中棱长为a，点E为AA1的中点，在对角面BB1D1D上取点M，使AM+ME最小，其最小值为.

题目分析在之前的解析几何中，学生学习过二维平面中求距离最短的方法——对称.因此在本题中，进行二维到三维的递进，根据图形的对称性，把AM+ME转化为CM+ME，然后利用两点之间线段最短求最小值.

解由对称性可知AM=CM，

所以AM+ME=CM+ME，

观察图形，可知当E，M，C三点共线时，CM+ME即AM+ME取得最小值，

最小值为CE=2a2+（a2）2=32a.

5结语

在这节课中，希望学生借助立体几何中的最短距离问题，体会数学“转化与化归”的思想，把看似不相关的两个问题联系在一起，便能够“最”有应得.