函数零点知识在数学解题中的应用

【摘要】在高中数学中，函数和方程之间存在着千丝万缕的联系，其中最重要的一种联系就是函数的零点.利用函数零点的定义，可以实现方程和函数之间的相互转化，进而将函数的零点问题转变为求解方程的根的问题，且求解方程的根的问题又转变为求解对应函数的零点问题.函数的零点问题在解答高中数学题中有很重要的作用，本文运用函数的零点知识分析和解决高中数学中常见的三类题型，希望能够帮助学生拓展新思路.

【关键词】函数零点；高中数学；解题方法

1判断方程存在实根

运用函数零点的知识判断方程是否存在实根，指的是当对应题目中的方程f（x）=0时，很难直接求出此方程的实根时，就可以通过分析此方程对应的连续函数y=f（x）的图象与横坐标轴是否存在交点，在图象上找出两个点，当这两个点满足一个点在横坐标上方，另一个点在横坐标下方即可判断方程在已知范围内存在实根.

例1已知方程x3－x2+1=0，那么在定义域－1，0内方程是否存在实根？并尝试说明理由.

解令f（x）=8c6bf7b1074fa99dd4e22a918bb60b36x3－x2+1，且函数f（x）是一条连续的曲线，

当x=－1时，f（－1）=（－1）3－（－1）2+1=－1<0；

当x=0时，f（0）=03－02+1=1>0，

因此，f（－1）·f（0）<0成立，

即等价于在定义域－1，0内，函数f（x）存在零点，

综上，方程x3－x2+1=0在区间－1，0内有实根.

2研究方程根的个数

运用函数零点的知识判断方程根的个数，指的是先将对应题目中的方程问题转变为函数问题，再利用函数的零点知识，即在已知区间内，函数y=f（x）存在f（a）·f（b）<0时，函数在区间内只有一个零点，然后利用函数的单调性即可判断出方程根的个数.

例2如果在区间－1，1内，函数f（x）=x3+bx+c单调递增，已知f－12·f12<0，那么，当f（x）=0在区间－1，1中（）

（A）可能含有三个实数根.

（B）可能存在两个实数根.

（C）存在唯一的实数根.

（D）没有实数根.

解因为f－12·f12<0，

根据零点存在性定理可知，函数f（x）=0在区间－12，12中存在实根，

且因为f（x）在区间－1，1内单调递增，

所以f－12<0，f12>0，

综上，方程f（x）=0在区间－1，1中只有一个实数根.

3求参数的取值范围

运用函数零点的知识求解参数的取值范围，指的是当对应题目中含有参数时，可以通过利用零点存在性定理和对应的函数图象即可求解出参数的取值范围.

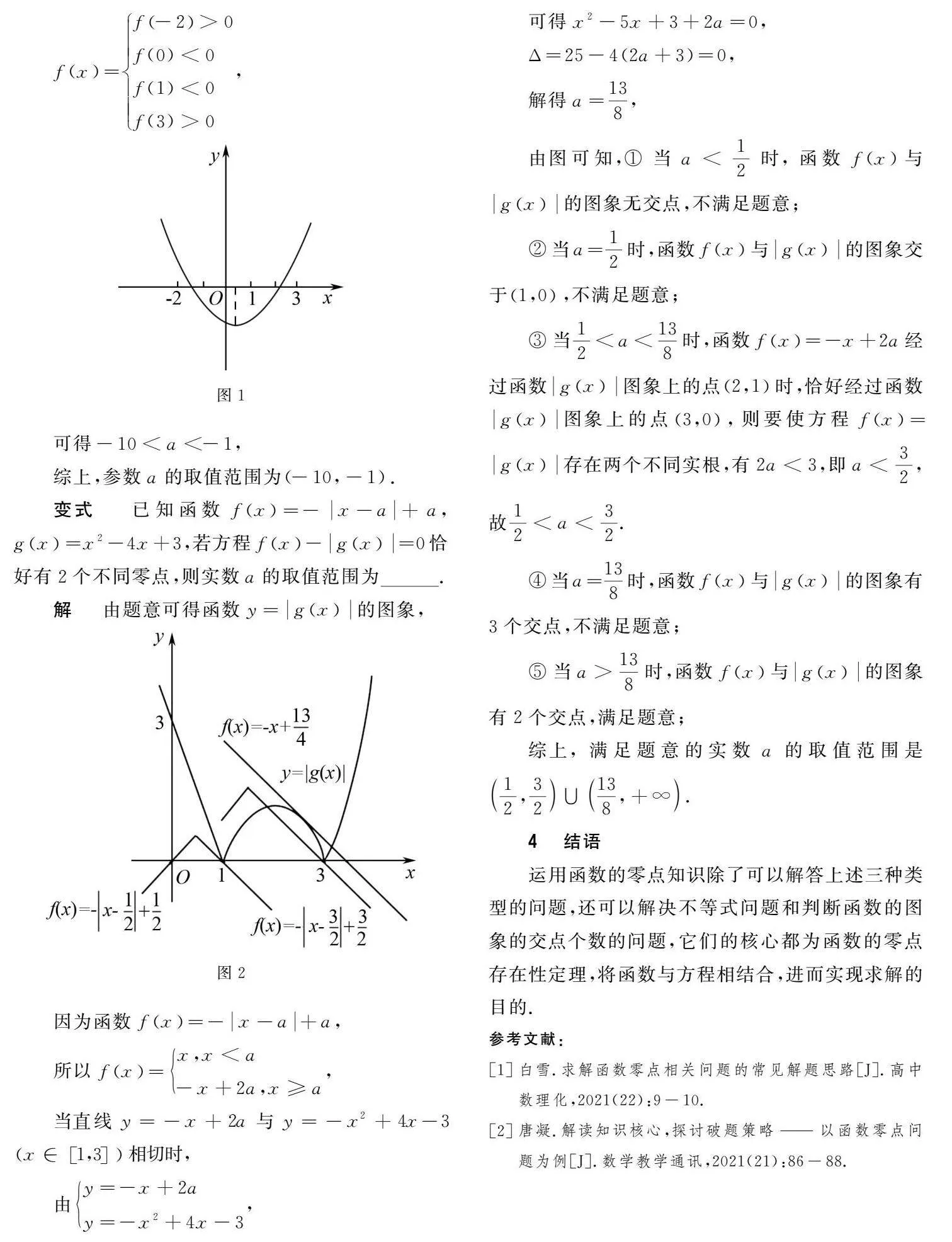
例3当函数f（x）=2x2－x+a存在两个零点时，已知一个零点在区间－2，0内，另一个零点在区间1，3内，试求出a的取值范围.

解由题意可得，函数f（x）=2x2－x+a，其图象如图1所示.

由题目条件和图1可知，

fx=f－2>0f（0）<0f（1）<0f（3）>0，

可得－10<a<－1，

综上，参数a的取值范围为－10，－1.

变式已知函数fx=－x－a+a，gx=x2－4x+3，若方程fx－gx=0恰好有2个不同零点，则实数a的取值范围为.

解由题意可得函数y=gx的图象，

因为函数fx=－x－a+a，

所以fx=x，x＜a－x+2a，x≥a，

当直线y=－x+2a与y=－x2+4x－3 x∈1，3相切时，

由y=－x+2ay=－x2+4x－3，

可得x2－5x+3+2a=0，

Δ=25－42a+3=0，

解得a=138，

由图可知，①当a＜12时，函数fx与gx的图象无交点，不满足题意；

②当a=12时，函数fx与gx的图象交于1，0，不满足题意；

③当12＜a＜138时，函数fx=－x+2a经过函数gx图象上的点2，1时，恰好经过函数gx图象上的点3，0，则要使方程fx=gx存在两个不同实根，有2a＜3，即a＜32，故12＜a＜32.

④当a=138时，函数fx与gx的图象有3个交点，不满足题意；

⑤当a＞138时，函数fx与gx的图象有2个交点，满足题意；

综上，满足题意的实数a的取值范围是12，32∪138，+∞.

4结语

运用函数的零点知识除了可以解答上述三种类型的问题，还可以解决不等式问题和判断函数的图象的交点个数的问题，它们的核心都为函数的零点存在性定理，将函数与方程相结合，进而实现求解的目的.

参考文献：

[1]白雪.求解函数零点相关问题的常见解题思路[J]．高中数理化，2021（22）：9-10.

[2]唐凝.解读知识核心，探讨破题策略——以函数零点问题为例[J]．数学教学通讯，2021（21）：86-88.