多网格下解析法计算石英灯辐射热流对比研究

关键词：多网格； 解析法； 辐射热流； 有限元法； 石英灯

中图分类号：V216.4 文献标识码：A DOI：10.19452/j.issn1007-5453.2024.10.008

石英灯加热装置是高速飞行器热结构地面热强度试验[1]中广泛采用的加热装置。加热装置设计的合理性直接关系到结构表面热载荷施加的准确性，可以通过计算石英灯阵列在结构表面产生的辐射热流分布情况来评估热载荷的均匀性、峰值水平以及其他分布特征等。

常用的石英灯阵列辐射热流计算方法包括解析法、蒙特卡罗法，以及采用基于上述方法的有限元软件工具等。采用有限元软件进行辐射热流计算的缺点主要有：（1）需要对大量的石英灯元件进行实体建模，需要设定受热结构表面与石英灯的复杂辐射换热关系，需要明确受热结构和石英灯的相关材料参数；（2）对于大规模石英灯阵列的辐射换热通常计算时间较长；（3）部分有限元软件中限制辐射换热单元总数，在进行大规模加热阵列计算时，对石英灯灯丝长度方向和环向的网格划分数量往往只能采取较为粗略的网格划分，在一定程度上影响计算结果的精度。孔凡金等[2]对比了区域法、离散坐标法、蒙特卡罗法等几种经典的辐射传热计算方法以及常用的辐射传热计算软件，讨论了几种辐射热流场计算模型的适用性，认为可根据计算目的和精度要求选择合适的计算方法，以实现对石英灯阵列热流场的快速准确模拟。

蒙特卡罗法通过光子轨迹追踪能够有效模拟光子在石英玻璃管内、反射屏作用下的复杂折、反射过程，因此计算精度较高，在辐射热流计算中应用十分广泛，国外很早便建立了采用蒙特卡罗法预测石英灯辐射热流的计算方法[3-5]，被国内学者广泛引用。宋伟浩等[6]利用蒙特卡罗法对红外灯阵出射光线进行了随机抽样和追迹，建立了受热平面上光线落点坐标数据库，计算了受热平面辐射照度分布情况。夏吝时等[7]采用蒙特卡罗法对平板形石英灯加热器中水冷反光板面积、水冷反光板与灯阵间距离、热源疏密程度、热源阵列与材料受热面间距等因素对辐射热场中典型隔热材料受热面温度分布均匀性和热流密度进行了模拟计算。朱言旦[8-9]基于蒙特卡罗法发展了石英灯阵辐射热流分布预测方法及计算程序，以灯阵中各灯功率为优化参数的石英灯阵热流模拟优化设计方法，对某飞行器结构部件迎风面气动加热进行了模拟。这些采用蒙特卡罗法的研究工作需要的输入参数较多、计算结果精度直接依赖于样本数量大小、计算时间相对较长等不足。

解析法基于斯忒藩-玻耳兹曼定律、兰贝特定律等传热学基本定律，求解时往往需要对研究对象进行简化，使之满足基本定律的应用条件，优点是显式计算过程收敛性好，通过模型简化可以实现较快的计算速度，同时可以根据需求进行编程扩展，缺点则是不能考虑光线在传播过程中复杂的折、反射现象。宋伟浩等[10]建立了红外灯阵辐照度分布数学模型和受热平面温度分布数学模型，针对灯间距离参数对受热平面温度分布进行了仿真与试验。李昕昕等[11]针对解析法不适用于带反射屏的石英灯辐射热流计算、蒙特卡罗法计算时间过长的问题，将蒙特卡罗法与解析法相结合，提出了基于解析法的“等效面光源”求解构想，首先采用蒙特卡罗法获得反射屏作用下的典型热流场分布结果，再利用辐射传热定律建立关于面光源各离散点温度的线性方程组，求解得到等效面光源的温度分布，之后采用解析法对等效面光源作用下的热流场进行计算，实现了带反射屏的石英灯加热装置的热流快速计算。张肖肖等[12]针对平板形、圆柱形、圆锥形石英灯加热阵列，提出了基于解析法的热流快速计算方法，构建了解析传热模型，建立了圆柱和圆锥加热阵列中单根石英灯管照射范围的判断依据，得到了典型灯管排布下热流分布规律。这种计算方法将灯丝半圆柱面作为平面处理，模型得到简化，计算速度显著提高，但在精度方面有所下降，需要进一步探讨半圆柱面多网格划分时的解析计算方法。

本文在参考文献[12]研究工作的基础上，建立适用于半圆柱面多网格划分时的热流密度解析计算方法，分析不同网格数量划分下热流分布差异，并与有限元软件热流计算结果进行对比，以评估该解析计算方法的正确性，同时探讨解析法在热流计算工程应用中的相关注意事项。

1 多网格时解析法计算理论

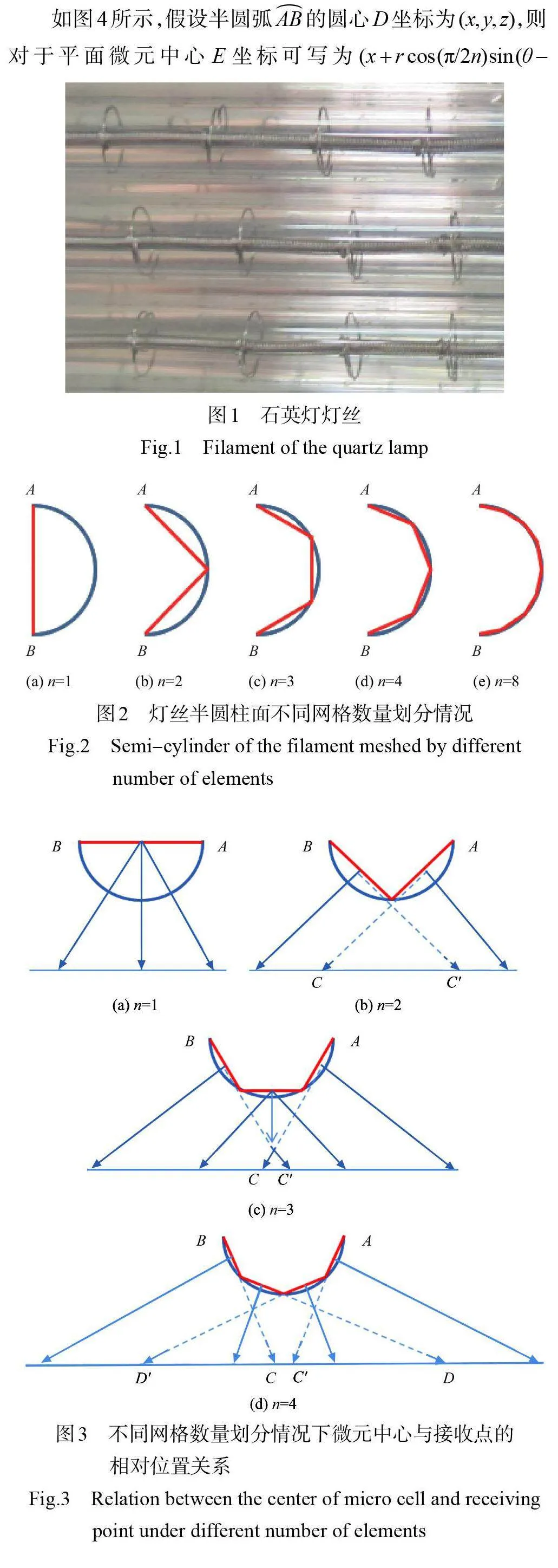
考虑灯丝面向试验件表面的半圆柱面（见图1），将灯丝沿长度方向N等分，对灯丝半圆柱面按照图2 采用数量为n的网格进行等分，将每一个弧面视为平面微元处理，把半圆柱面发出的总热流平均到每段平面微元上，则每段微元对外发出热流

式中， r 为灯丝半径；L 为灯丝长度；N为灯丝沿长度方向均分数量；σ 为斯忒藩-玻耳兹曼常数；T为灯丝温度。

从图3可以看到，各微元中心位置与接收面上不同位置的接收点之间的相对关系呈现出更为复杂的变化，n=1 时，可认为所有接收点均可受到平面微元的照射，而当n>1 时，对于非水平位置的平面微元，在接收面上均存在一个其微元对应半球空间能够产生照射的极限位置，即微元所在平面与接收面的交点位置（如图3中的C和C'、D和D'）。

将不同θ位置的各段平面微元对G点产生的热流密度累加，便得到了在单根石英灯作用下G点的热流密度。对于多根石英灯组成的阵列，可以按照上述过程逐根计算每根石英灯对各接收点产生的热流密度再累加，便可以得到不同网格数量划分下的热流密度场分布情况。

2 计算结果

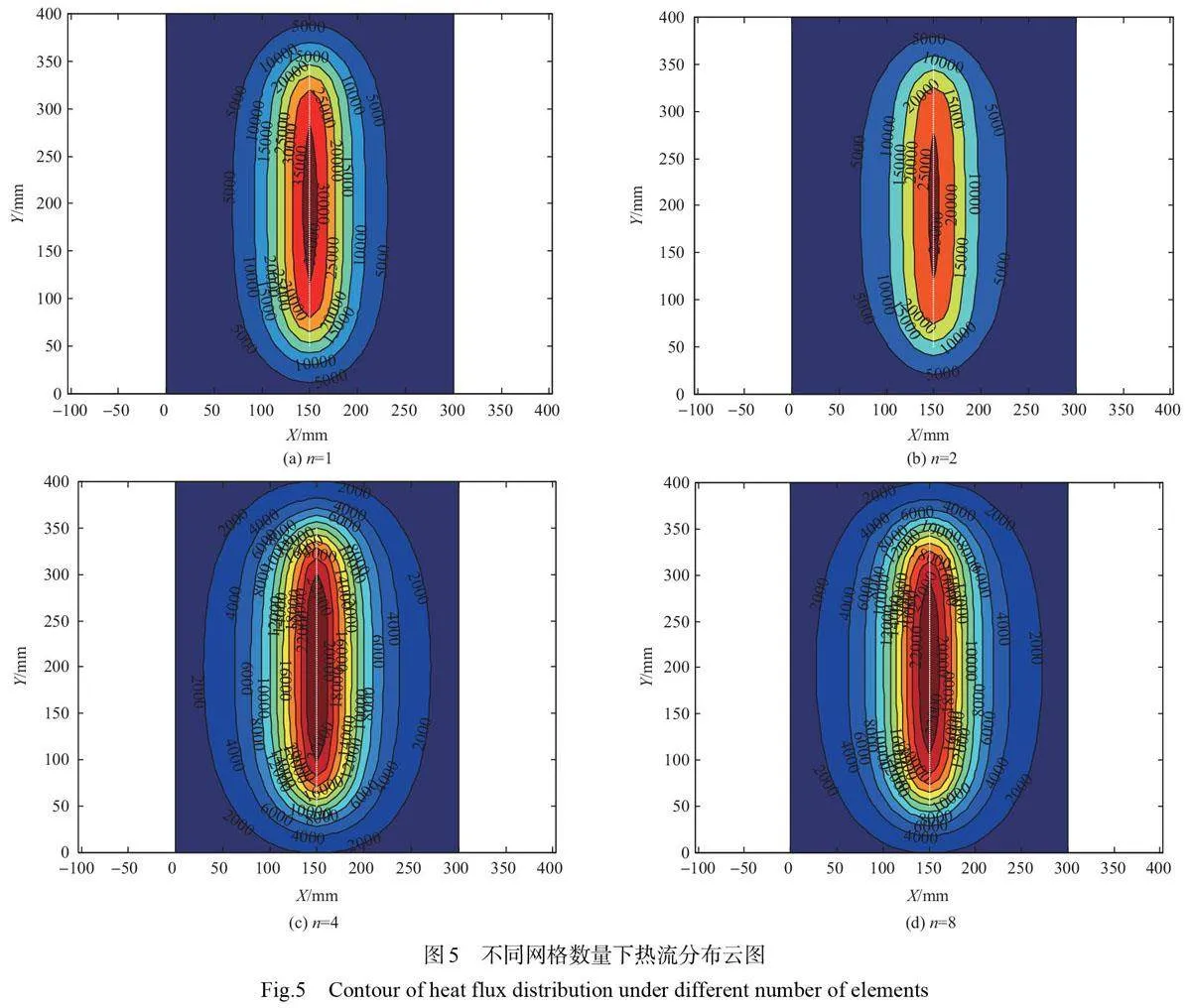
计算长度300mm、直径2.6mm、距接收面高度50mm的单根石英灯灯丝在300mm×400mm区域的热流分布情况，接收面长度和宽度方向每10mm选取一个节点，灯丝沿长度方向等分为100 段，灯丝温度取2000K，计算得到不同网格数量下的热流分布云图如图5 所示，图中白色虚线为灯丝在接收面上的投影。可以看到当n 从1 增加到4 时，热流分布以及热流峰值水平呈现出相对显著的变化，而当n 从4继续增加后，热流分布以及热流峰值水平相对变化不明显。

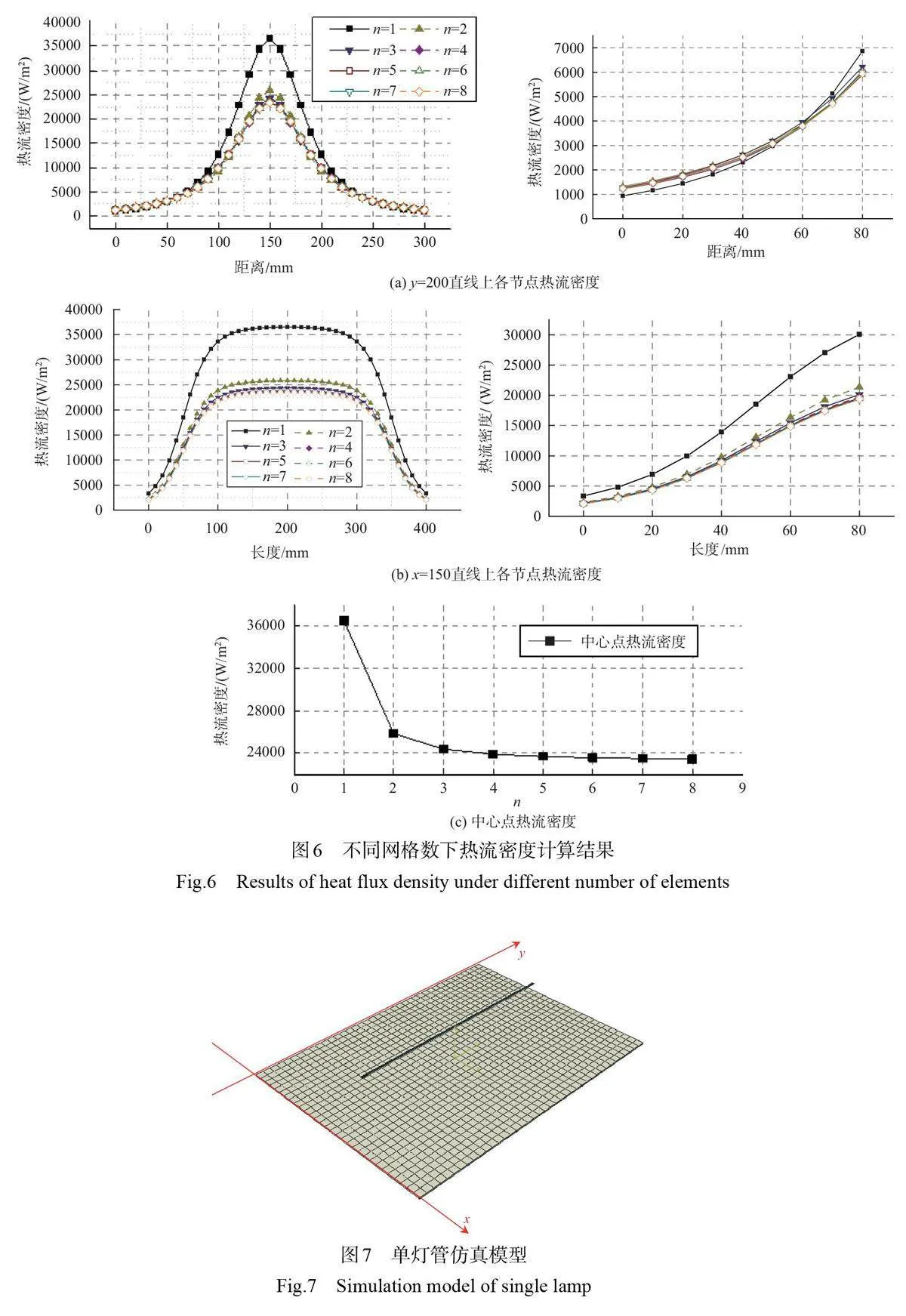
提取上述云图中y=200 以及x=150 两条直线上各节点以及坐标为（150，200）的中心点的热流密度计算结果，如图6 所示。可以看到，随着n 的增大，热流密度峰值逐渐减小，当n 从1 增加到2 时，热流密度峰值变化尤为明显，当n 从4继续增加后，峰值水平逐渐趋于稳定；与中心点处相反，坐标为（0，200）和（300，200）的左右边缘处热流密度，当n=1 时取得最小值；而坐标为（150，0）和（150，400）的上下边缘处热流密度随着n 的增大，呈现出与中心点处相似的变化趋势。这是由于当n=1 时灯丝所有辐射能量集中于一个矩形窄带内，根据兰贝特（Lambert）定律，此时灯丝对正下方区域的定向辐射强度达到最高值，而对左右边缘处的辐射作用受较小的可见面积影响相对最弱；而随着n 的增加，灯丝的辐射能量均匀分散于沿环向的各矩形窄带内，灯丝对正下方区域的辐射强度逐渐降低，但由于两者间距离最短，所以正下方区域的热流密度仍然达到当前分布的最高值，而对左右边缘处的辐射作用受到环向窄带对其可见面积增大的影响相对n=1 有了一定增强，但受到可对其照射的窄带数量降低的影响，增强幅度较小；随着n 的增加，环向窄带对上下边缘处的可见面积相对n=1 进一步降低，因此上下边缘处受到的辐射作用当n=1时达到最强。

3 有限元计算结果对比

3.1 热流计算结果对比

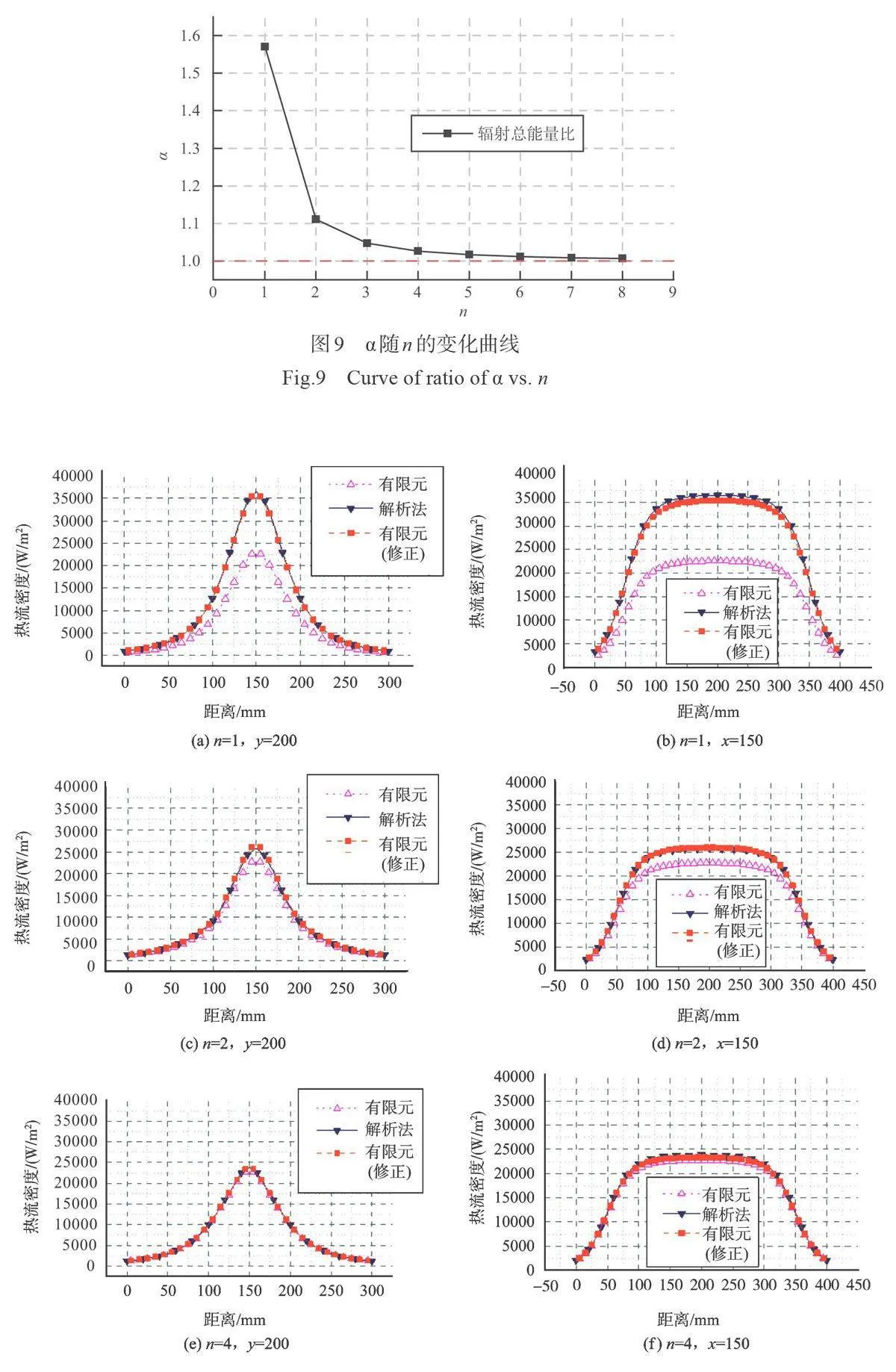
目前，商用有限元软件在石英灯辐射热流计算中被广泛采用，将解析法计算结果与相同参数条件下的有限元计算结果进行对比，通过结果的一致性可以验证解析法的正确性。采用与第2 节中相同尺寸、高度和温度的灯丝以及相同大小的接收面，接收面网格尺寸为10mm×10mm，灯丝沿长度方向等分为100个网格，按照面面辐射法在有限元软件计算不同环向网格数量下的热流密度分布，计算模型如图7 所示。同样提取横竖中轴线上的热流分布结果，与解析法计算结果进行对比，如图8 所示。从图8 中可以看到，当n=1 时（此时灯丝有限元模型与解析法模型均为矩形窄带），解析法与有限元软件计算结果呈现出显著差异，峰值热流水平相对误差达到61.7%；随着n 的增加（此时灯丝有限元模型与解析法模型均为半圆柱面，并且环向网格数相同），两种方法的热流计算结果的差异逐渐缩小，当n>4时，计算结果一致性相对保持稳定；与解析法计算结果不同，有限元软件计算得到的中心点处热流密度随着n 的增大呈现出小幅的增大。

因此，灯丝对外辐射总能量差异应是解析法与有限元热流计算结果差异的最主要原因。α 随n 的变化如图9 所示，从图9 可以看到，随着n 的增大，辐射总能量之比逐渐趋近于1；当n=1 时，解析法中辐射总能量是有限元软件中的1.57 倍，在相同灯丝温度情况下，有限元软件中采用灯丝直径宽度的矩形窄带来计算石英灯辐射传热会显著降低结构温度响应的精度；当n=3 时，辐射总能量之比达到1.047，n=4 时，辐射总能量之比达到1.026，因此建议在有限元建模时对灯丝半圆柱至少采取3～4个的网格进行划分。

为验证解析法的有效性，将有限元计算中的灯丝温度结合式（9）进行调整，以保证二者在计算过程中灯丝对外辐射总能量一致，进而通过对比验证解析法计算结果的正确性。将有限元计算中的灯丝温度T调整为式（10）中的T

式中，T为调整后的有限元计算中灯丝温度；T 为给定的石英灯灯丝温度。

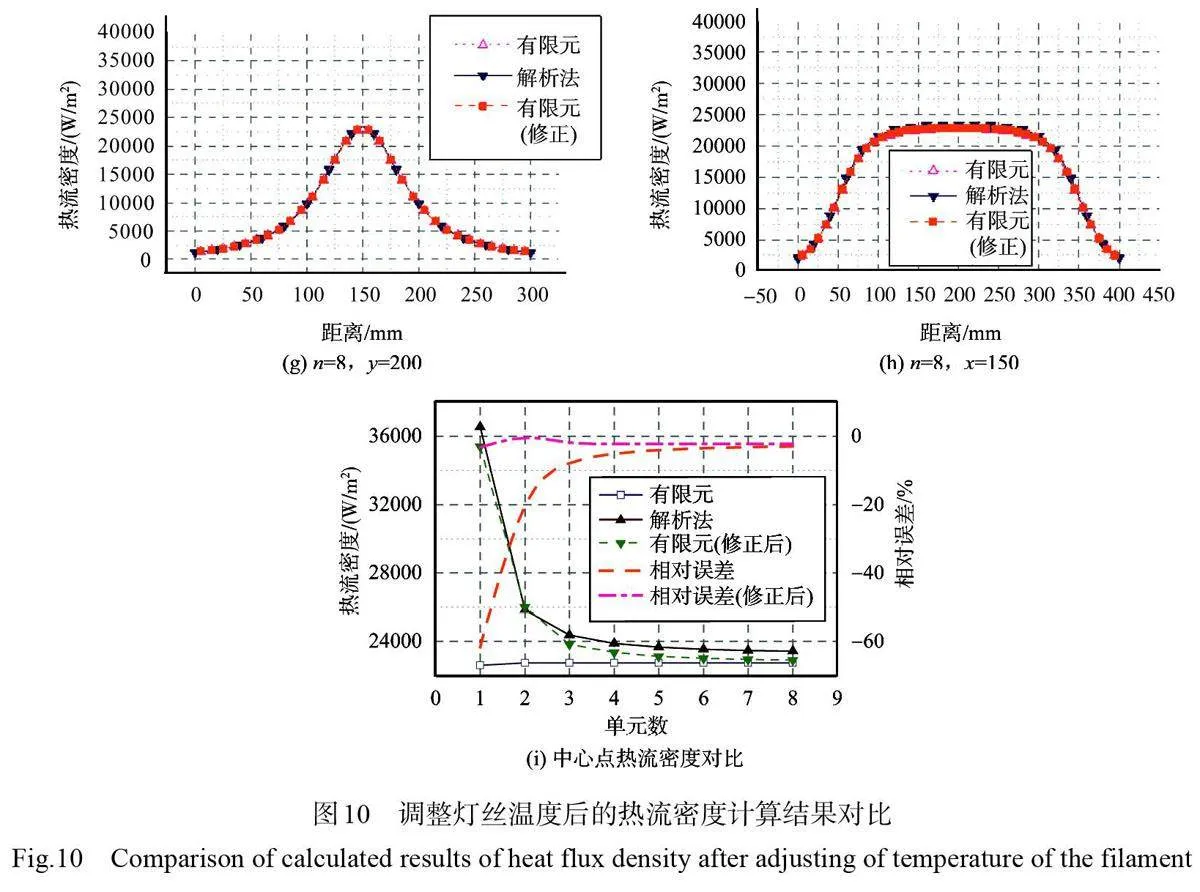
3.3 调整灯丝温度后的热流计算结果对比

对有限元模型中的灯丝温度按照式（10）调整后，重新计算并对比解析法与有限元计算热流密度结果，如图10所示。从图10可以看到，经过灯丝温度调整、保证辐射总能量一致后，有限元计算结果与解析法计算结果的一致性相对调整前得到显著改善，n=1 时中心点热流密度相对误差仅有3.23%。其他产生误差的原因可能是有限元软件中热流密度为单元计算结果，此处的节点热流密度结果是将其相邻单元的结果进行平均得到，而解析法计算结果则是该节点位置的理论计算结果，两者存在一定偏差。

4 结论

针对石英灯辐射热流计算，本文提出了适用于半圆柱面多网格划分时的解析计算方法，对比了与有限元软件热流计算结果的差异，确定了差异产生原因并建立了调整方法，验证了解析计算方法的正确性，得到了以下结论：

（1）采用解析法计算石英灯热流密度分布时，采用不同的网格数量划分灯丝半圆柱面会对计算结果产生影响，当n≥4后，热流密度峰值水平逐渐趋于稳定。

（2）n=1 时采用解析法计算石英灯热流密度虽然计算精度相对较差，但由于灯丝网格数量较少且不存在照射范围判断问题，在同等计算条件下能够获得最快的计算速度，因此在大规模石英灯阵列的辐射热流预估中仍然有其工程应用价值；当n 达到3 以上时，解析法计算结果可以满足工程中对石英灯热流仿真计算精度的要求。

（3）在相同灯丝温度情况下，有限元软件中采用灯丝直径宽度的矩形窄带来计算石英灯辐射传热会显著降低结构温度响应的精度，因此在有限元建模时对灯丝半圆柱面至少采取3～4个的网格进行划分。

（4）灯丝对外辐射总能量差异是解析法与有限元热流计算结果差异的最主要原因，将灯丝温度按照总能量比进行调整后，解析法与有限元计算结果的一致性得到大幅改善，证明了本文提出的多网格时热流密度解析计算方法的正确性。

（5）采用本文提出的解析法计算的热流密度值可作为热流载荷边界施加于有限元分析模型中，从而省去在有限元软件中对石英灯建模的过程，同时可以不受部分有限元软件对辐射换热单元总数的限制，能够满足大尺度结构与大规模石英灯阵列辐射传热下结构温度响应快速计算的需求。