发电厂电气一次主接线元件可靠性评估模型

摘 要：发电厂一次主接线元件涵盖变压器、发电机、输电线路、断路器等，各类元件的可靠性直接影响电力供应。为了准确评价以上电气元件的可靠性，研究过程以马尔可夫状态转移理论为基础，建立了四状态和五状态的可靠性评估模型，对应的状态类型包括正常运行、计划检修、非扩大型故障、扩大型故障、隐性故障。对模型进行求解，可计算各个电气元件处于不同状态的概率，当正常运行状态的概率越大时，代表该元件的可靠性越高。完成建模后，以国内某水力发电厂的主接线元件为分析对象，成功地计算了不同元件在各个状态下的概率，验证了该评估模型的有效性。

关键词：发电厂；电气一次主接线元件；可靠性评估模型；模型求解方法

中图分类号：TM 732 " 文献标志码：A

发电厂的安全性、供电连续性和供电充裕性与各类电气一次主接线元件的可靠性存在密切的关联，当部分元件出现故障时，有可能导致发电中断，影响电网的平稳运行。因此，在电力运维管理工作中，需要建立针对一次主接线元件的可靠性评估方法。

常用的可靠性评价方法包括故障树法、状态枚举法、蒙特卡洛法，但电力系统较复杂，导致以上3种评价方法产生较大的运算量，制约了运算效率。为了解决该问题，在此次研究中，以马尔可夫状态转移理论为基础，结合断路器、变压器、发电机等发电系统元件的故障特点，建立了包括多种状态的可靠性评估模型。与传统评价方法相比，该模型的优点为数据量小，可利用软件工具辅助计算。

1 发电厂电气一次主接线元件可靠性评估方法设计

发电厂电气一次主接线元件主要是指各种一次设备，包括发电机、变压器、母线、断路器等。当构建一次元件的可靠性评估模型时，采用马尔可夫状态转移理论。根据该理论的思想，一次主接线元件的运行过程总是在不同状态之间转移，其运行状态包括正常、计划检修、非扩大性故障、扩大性故障等[1]。

1.1 输电线路、变压器、发电机的可靠性评估模型构建

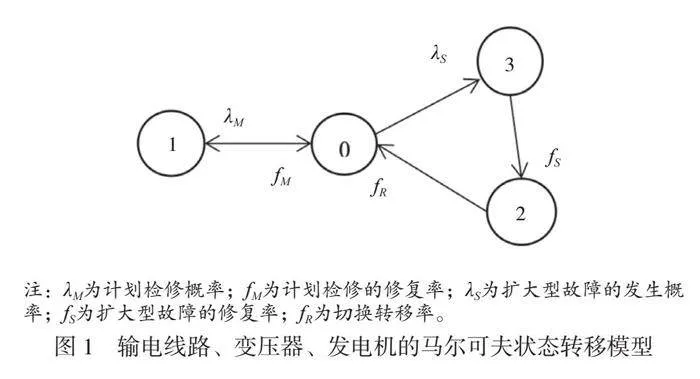
输电线路、发电机和变压器均属于重要的一次设备，其状态转移关系基本一致，因此可建立如图1所示的马尔可夫状态转移模型。在该模型中，0代表电气元件处于正常状态，1代表电气元件处于计划检修状态，2代表电气元件处于非扩大型故障状态，3代表电气元件处于扩大型故障状态[2]。该状态转移模型能够求解发电机、变压器和输电线路在各种状态下的概率，从而判断其可靠性。

1.2 断路器的可靠性评估模型构建

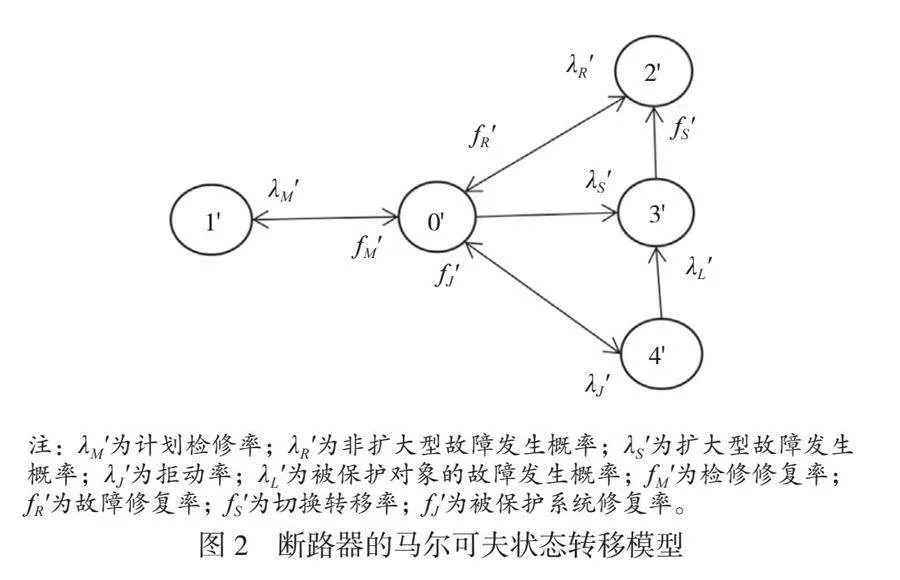
断路器具有切换功能，可改变电力系统的复杂度，其常见的故障类型包括接地故障、相间短路、保护气体泄漏、烧毁等。根据马尔可夫状态转移理论，对断路器的各种故障进行归类，可建立如图2所示的状态转移模型。在该模型中，0'代表断路器处于正常正态，1'代表断路器处于计划检修状态，2'代表断路器处于非扩大型故障状态，3'代表断路器处于扩大型故障状态，4'代表断路器处于隐性故障状态[3]。该模型描述了断路器各个状态之间的转移关系，可用于计算各状态的发生概率，从而判断断路器的可靠性。

1.3 可靠性评估模型求解方法

图1的模型包括4种状态，图2的模型包括5种状态，模型的求解难度与状态的数量呈正相关。不同的状态代表相互排斥的事件，有利于状态求解。四状态模型和五状态模型的求解原理相同，但求解过程存在差异。以下介绍断路器可靠性评估模型的求解方法。

根据图2的模型可以建立断路器的马尔可夫状态转移矩阵，如公式（1）所示。

（1）

式中：Λ为断路器的马尔可夫状态转移矩阵。

在系统稳态条件下，将图2中5种状态（0～4）的发生概率分别记为P0、P1、P2、P3、P4。由于5种状态涵盖了断路器的所有运行状态，因此5种状态的概率之和为1，即P0+P1+P2+P3+P4=1[4]。同时，P0～P4满足公式（2）。

（2）

对公式（2）进行求解，即可得到断路器5种状态的发生概率。在实际应用过程中，可利用MATLAB软件编写程序，对以上方程进行求解，具体实施过程中，需要根据电气系统的历史数据采集模型中的各类参数，包括λM'、λR'、λL'、fM'、fR'等[5]。

2 可靠性评估模型应用实例

2.1 发电厂及其电气一次主接线元件概况

国内某发电厂采用水轮电机组，单个机组的发电机装机容量达到180MW，总装机容量达到360MW。每套机组由2台发电机组成，分别为60MW和120MW的水轮发电机。该发电厂的一次主接线设备包括母线、进线、出现、联络断路器、发电机、变压器。母线的电压等级为220kV，燃气发电机的配套变压器为242/15kV，蒸汽发电机的配套变压器为242/10.5kV。该电厂的电气一次主接线电路如图3所示，电气一次主接线元件分类汇总见表1。

2.2 可靠性评价模型输入参数采集

在建立各个电气元件的可靠性评价模型后，需要根据该发电厂的历史运行数据，计算各个一次主接线元件的可靠性评价模型原始参数。该发电厂一次主接线电气元件的数量较多，总计达到18个，限于篇幅，表2对部分电气元件的可靠性评价模型原始参数进行汇总。

2.3 可靠性模型求解

2.3.1 模型求解过程

研究过程使用MATLAB软件编写计算机程序，对此次建立的可靠性评估模型进行求解。以公式（2）为基础，令矩阵P=[P0 "P1 "P2 "P3 "P4]。求解时从矩阵Λ中随机删除任意一列，再对处理后的矩阵Λ与单位矩阵e进行增广处理。其中，单位矩阵e=[1 1 1 1 1]T。经过增广处理后，相当于增加了一个新方程，将Λ与单位矩阵e增广处理后得到的新矩阵记为U[6]。此时可利用矩阵U、P建立一个等式，如公式（3）所示。

（3）

式中：U为Λ与单位矩阵e增广处理后得到的新矩阵；矩阵k=[0 0 0 0 1]。

利用MATLAB软件对公式（3）进行求解，求出向量P，即可判断该发电厂各类一次主接线元件在不同状态下的概率情况[7]。

2.3.2 各类一次主接线元件的可靠性求解

2.3.2.1 水轮发电机可靠性求解结果分析

水轮发电机为G1、G2、G3、G4，对应图1的四状态模型，因此求解结果为P0、P1、P2、P3。表3为4台水轮发电机组各个状态的求解结果。由数据可知，该发电厂4台水轮发电机处于正常状态的概率分别为94.39%、93.22%、93.22%、94.39%。4台水轮机处于需要检修状态的概率次之，均不超过7%。水轮机处于非扩大型故障状态和扩大型故障状态的概率都非常低。

2.3.2.2 断路器可靠性求解结果分析

断路器元件对应图2的五状态马尔可夫模型，概率求解结果为P0、P1、P2、P3、P4，图4为各个断路器处于正常状态的概率。由数据可知，CB18、CB19断路器的可靠性最高，其处于正常运行状态的概率达到97.29%。CB5、CB6、CB11、CB12、CB13、CB14、CB17断路器的可靠性基本相当，其处于正常运行状态的概率均略高于95%。

2.3.2.3 变压器可靠性求解结果分析

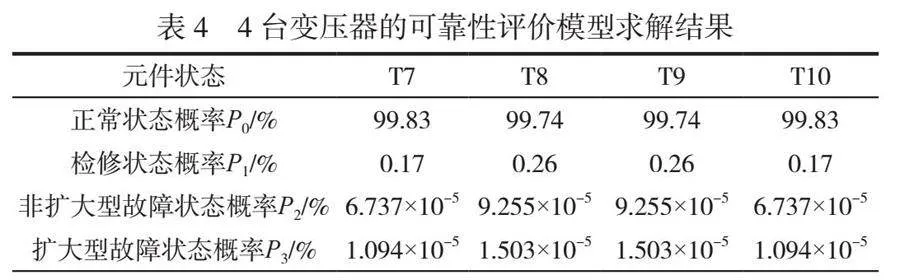
变压器元件的马尔可夫转移状态为四状态模型，利用软件工具对其可靠性评估模型进行求解，得到各个变压器处于P0、P1、P2、P3状态的概率，结果见表4。由数据可知，4台变压器处于正常运行状态的概率分别达到99.83%、99.74%、99.74%、99.83%，可靠性均较高。4台变压器处于非扩大型故障状态和扩大型故障状态的概率均非常低。

2.3.2.4 出线可靠性求解结果分析

L20、L21为发电厂出线，其马尔可夫状态转移模型为四状态模型。L20出线的P0～P4求解结果分别为0.8620、0.1353、0.0027、4.92×10-6。L21出现的P0～P4求解结果与L20出线完全相同。与断路器、变压器、水轮发电机相比，2条出线的可靠性相对较低，仅达到86.2%，差距约为10个百分点。

3 结语

在此次研究中，针对发电厂的各种电气一次主接线元件，包括变压器、断路器、输电电路、发电机，建立了基于马尔可夫状态转移理论的可靠性评估模型，旨在判断各个电气元件的运行状态及可靠性。根据研究内容，得出以下基本结论。1）以马尔可夫状态转移理论为基础，根据电气元件的故障特点，可将其所处的状态划分为5种类型，分别为正常状态、检修状态、非扩大型故障状态、扩大型故障状态和隐性故障状态。断路器的故障状态较多，并且能够改变电力系统的拓扑结构，因此采用五状态可靠性评估模型。变压器、输电线路、发电机、母线可采用四状态可靠性评估模型。2）当求解模型时，根据马尔可夫状态转移模型中的参数建立矩阵，该矩阵与5种状态对应的概率向量的乘积为0。可据此建立方程，从而求解电气元件处于5种状态的概率。当正常运行状态的概率值越大时，代表该电气元件的可靠性越高。3）在模型求解前，需要采集各种模型参数的历史数据，包括计划检修率、检修修复率、非扩大型故障发生概率、扩大型故障发生概率、故障修复率、切换转移率、被保护对象修复率等。这些数据为可靠性评估模型的输入参数，通过矩阵方程运算，可求解电气元件在各个状态的概率值。

参考文献

[1]聂岩，樊潇，吕冠成.铅山抽水蓄能电站电气主接线可靠性计算[J].电工技术，2024（4）：187-189.

[2]张宇航，欧阳名三.基于故障树分析的电缆故障诊断可靠性评估方法研究[J].佳木斯大学学报（自然科学版），2024，42（4）：28-31.

[3]李兆宇，武紫梁.基于人工智能的电气工程故障预测与可靠性评估策略分析[J].集成电路应用，2024，41（1）：338-340.

[4]何天玲.基于业务N–2的电力通信网可靠性评估方法研究[J].电力信息与通信技术，2021，19（2）：36-43.

[5]贾凯，任惠，郑至斌.基于设备时变故障率的海上油田电力系统可靠性评估[J].电力科学与工程，2022，38（1）：31-40.

[6]魏江英，董义俊，刘振祥.改进型MTBF-T模型的电子设备可靠性评估方法[J].单片机与嵌入式系统应用，2023，23（12）：63-66，75.

[7]葛梦昕，汪雪.基于GO法的智能变电站继电保护可靠性评估研究[J].光源与照明，2023（9）：204-206.