基于Simulink的直驱式风力发电机控制系统仿真

摘 要：本文针对直驱式风力发电控制系统的仿真问题，研究风力机和永磁同步发电机的数学模型，构建基于MATLAB/Simulink的直驱式风力发电机控制系统整机仿真模型，分别以阶跃风和随机风作为仿真计算工况，得到系统的风能利用系数。仿真结果表明，本文建立的仿真模型能够能快速追踪在不同工况下的风速变化，模拟在不同工况下系统对风速的响应过程，仿真结果准确、可靠，能够为控制系统的性能分析和过程优化提供理论依据。

关键词：风力发电；控制系统；风能利用系数；仿真

中图分类号：TM 315 " " " " " " 文献标志码：A

风力发电是风能利用的主要方式之一。直驱式风力发电机系统具有装置简单、能量利用率高等优点，发展迅速。风能存在随机性、间歇性和波动性，风力发电机的输出功率也具有不稳定性，因此，直驱式风力发电顺利并入电网系统的重要途径是对不同风速进行最大功率自适应控制。其中，研究风电场动态特性、进一步了解风力发电系统的基础是建立风力机和永磁同步发电机数学模型，构建直驱式风力发电机系统仿真模型。

电磁暂态仿真是风力发电系统时域仿真的主要方法之一，其包括节点分析法和状态变量分析法[1]。其中，状态变量分析法应用范围更广，并以MATLAB/Simulink环境为典型仿真环境。虽然许多学者研究基于MATLAB/Simulink环境的风电系统仿真[2-3]，但是随着风电系统组成元器件不断增多，系统混杂性凸显，导致现有仿真模型在适用性、开放性方面仍然存在较大不足。

综上所述，构建风力机数学模型和永磁同步发电机数学模型，研究基于MATLAB/Simulink的直驱式风力发电机控制系统仿真建模，对保证风力发电机稳定运行、推动海上风电产业发展有重要作用。

1 数学模型

当构建直驱式风力发电机控制系统时，需要分别建立风力机和永磁同步发电机的数学模型。

1.1 风力机数学模型

风力发电机系统包括空气动力学系统、机械系统、发电机系统、控制系统和桨距角执行系统等[4]。在风力的驱动下，风力机叶片开始旋转，将风能转换为机械能，利用发电机系统将机械能转换为电能输出。控制系统的作用是合理控制风力机的桨距角和转矩，使风力发电机控制系统稳定地运行[5]。

在风能的作用下，风力机的输出功率Pm的计算过程如公式（1）所示。

（1）

式中：ρ为空气密度，kg/m3；Cp为风能利用系数；R为风力机叶片半径，m；v为风速，m/s。此时，如果已知风力机的机械角速度ω，那么风力机输出的机械转矩Tm的计算过程如公式（2）所示。

（2）

Cp体现了风力机对风能的利用效率，其计算过程如公式（3）所示。

Cp=0.517 6（116λi-0.4β-5）e-21λi+0.006 8λ " " " " " " " " "（3）

式中：λi为中间变量；β为浆距角，°；λ为叶尖速比。根据公式（4）和公式（5）确定λ和λi的值。

（4）

（5）

式中：n为风力机转速， r/min。当β恒定时，Cp随着λ增大先增大后变小。当Cp为最大值时，对应的λ为最佳叶尖速比λopt。当λ恒定且λ=λopt时，Cp随着β增大而变小。因此，当λ=λopt时，β=0°，此时Cp达到最大值。基于此，实时监测v，调整n，使其满足λ达到λopt的条件，Cp取得最大值，使风力机输出功率达到最大值的方法即最佳叶尖速比法[6]。使用该方法能够保证风力发电机系统在不同工况下高效、稳定地运行。

1.2 永磁同步发电机数学模型

永磁同步发电机是一个时变非线性系统，进行风力发电机系统仿真建模的基础是建立其数学模型。为降低模型复杂度和计算难度，在建立永磁同步发电机数学模型的过程中进行以下4个假设。1）忽略磁路饱和、涡流损耗和滞后损失的影响。2）定子三相绕组呈对称布置，磁场呈正弦分布。3）转子绕组无阻尼作用。4） 电路元件为理想元件。永磁同步发电机定转子空间的3种坐标系分别为三相静止abc坐标系、两相静止αβ坐标系和两相旋转dq坐标系（如图1所示）。

在理想工作状态下，abc坐标系的a、b和c相在空间呈对称分布，任意两相之间的夹角为120°；在αβ坐标系中，β轴与α轴夹角为90°，α轴与a轴同方向；在dq坐标系中，q轴与d轴夹角为90°，d轴与a轴之间的夹角θ即转子的位置角，决定dq坐标系中的矢量坐标。

在abc坐标系中，在t时刻，永磁同步发电机的定子电压方程如公式（6）所示。

（6）

式中：ua、ub和uc分别为abc坐标系中各相定子绕组电压；Ra、Rb和Rc分别为各相定子绕组电阻；ia、ib和ic分别为abc坐标系中各相定子绕组电流；La、Lb和Lc分别为各相定子绕组自感系数；Lab、Lac、Lba、Lbc、Lca和Lcb分别为各相定子绕组互感系数。永磁同步发电机的三相定子绕组对称布置，因此两相定子绕组之间的互感系数相等，如公式（7）所示。

（7）

θ与ω的关系如公式（8）所示。

θ=ωt " " " " （8）

根据以上分析可知，在abc坐标系中，三相电压方程为微分方程，当系统分析时直接计算比较困难。为降低计算复杂度，需要在abc坐标系、αβ坐标系和dq坐标系之间进行变换，包括Clarke变换及其逆变换、Park变换及其逆变换[7]。Clarke变换用于abc坐标系至αβ坐标系的信号变换，其电流信号变换计算过程如公式（9）所示。

（9）

式中：iα、iβ为αβ坐标系中的电流。

Clarke逆变换用于αβ坐标系至abc坐标系的信号变换，其电流信号变换如公式（10）所示。

（10）

Park变换能够将电压或电流信号从αβ坐标系变换至dq坐标系，其电流信号Park变换计算过程如公式（11）所示。

（11）

式中：id、iq为dq坐标系中的电流。

相反，Park逆变换能够将电压或电流信号从dq坐标系变换至αβ坐标系，其电流信号Park逆变换计算过程如公式（12）所示。

（12）

同理，可以计算各坐标系中电压信号的变换关系。

2 仿真建模

风力发电控制系统的仿真分析需求促进风力发电控制系统模型的不断发展。对建立的仿真模型进行试验，获得风力发电控制系统的动态行为与内在规律。基于上述风力机数学模型和永磁同步发电机数学模型，在MATLAB/Simulink仿真环境中分别建立风力机仿真模型和永磁同步发电机仿真模型。

风力机仿真模型如图2所示。风力机仿真模型为整机仿真模型的子模型。根据风力机数学模型得到仿真模型的输入参数为ρ、R、v、n和β。结合永磁同步发电机数学模型的输入参数，确定风力机仿真模型的输出参数为Tm、Cp和Pm。

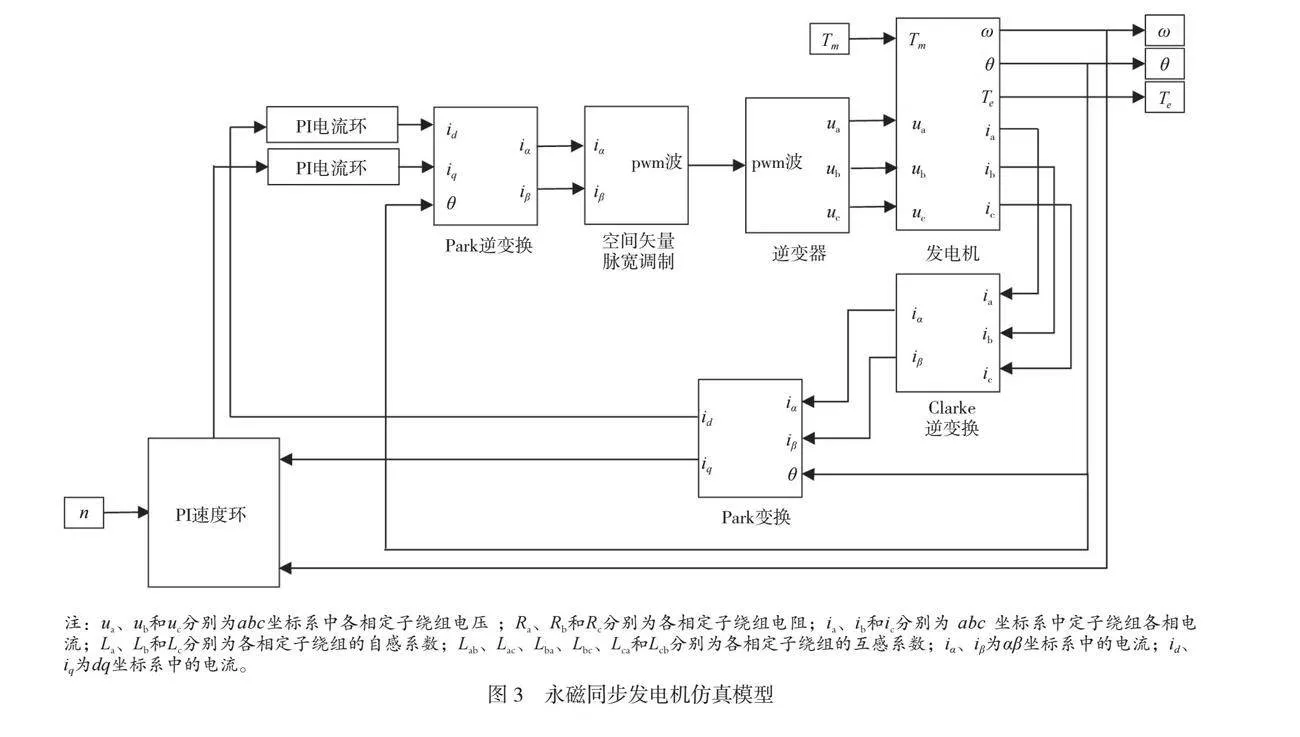
永磁同步发电机仿真模型如图3所示。该模型是由永磁同步发电机、Clarke逆变换、Park变换、Park逆变换、PI速度环、PI电流环、空间矢量脉宽调制以及逆变器等模块组成的。模型的输入参数包括Tm、n。仿真输出参数包括ω、θ、ia、ib、ic 和实时输出转矩Te。

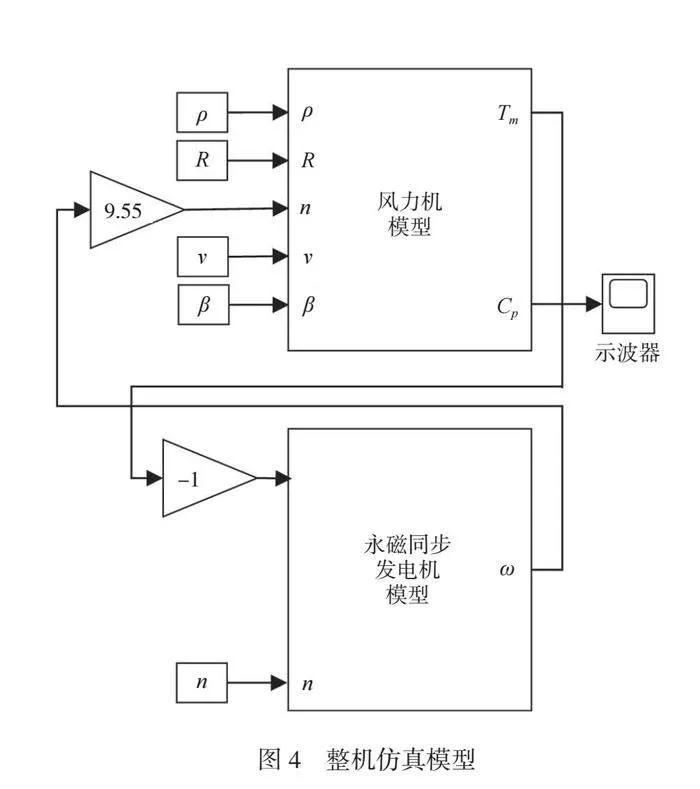
基于建立的风力机仿真模型和永磁同步发电机仿真模型建立直驱式风力发电机控制系统整机仿真模型，如图4所示。其中，ρ=1.225 kg/m3，R=44 m， β=0°，n=18 r/min。

3 仿真结果与分析

基于上述仿真模型，分别在阶跃风工况和随机风工况下对直驱式风力发电控制系统进行仿真，以验证模型的可行性和有效性。

3.1 阶跃风工况仿真

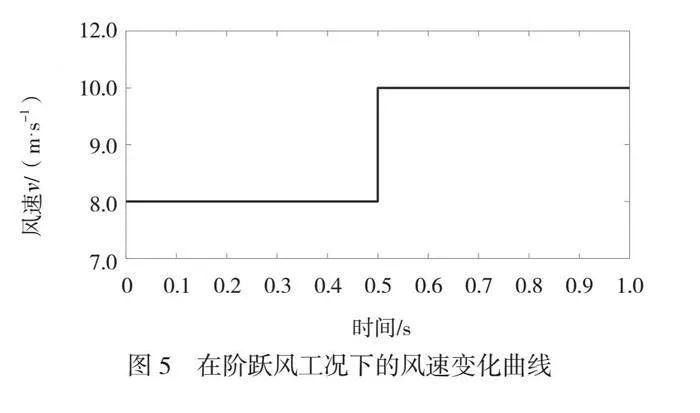
阶跃风工况模拟直驱式风力发电控制系统在工作过程中当突遇风速大幅度变化时的响应。在阶跃风工况下风速变化曲线如图5所示。仿真时间为1.0 s，初始风速为8.0 m/s，当t为0.5 s时，风速阶跃为10.0 m/s。

在阶跃风工况下，仿真得到系统的风能利用系数变化曲线如图6所示。由图6可知，由于风力发电机控制系统具有非线性的特点，因此当风速变化时，系统的风能利用系数Cp会有一定的超调和波动。因为系统初始状态为静止状态，所以在仿真初始阶段，Cp从0开始逐渐上升，经过短暂波动后，升至约0.408 1，并有微小波动。当t为0.5 s时，Cp经过波动后升至约0.423 2，并有微小波动。结果表明，仿真模型能够有效模拟风速突变的实际工况，仿真结果准确、可靠。

3.2 随机风工况仿真

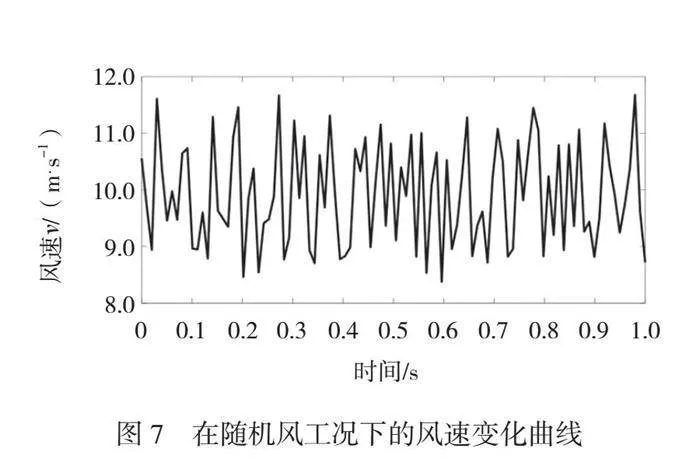
在实际工作过程中，风速总是随着时间发生变化，因此引入随机风工况。本文采用在随机风工况下的风速变化曲线如图7所示。由图7可知，在仿真时间为1 s的过程中，风速为8 m/s～12 m/s。

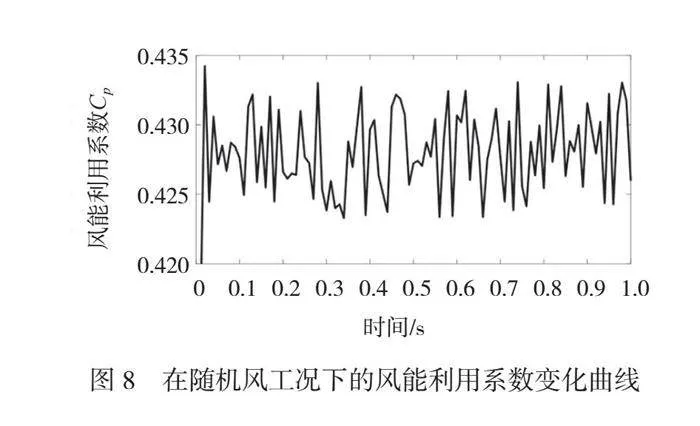
在随机风工况下，仿真得到的风能利用系数变化曲线如图8所示。由图8可知，随着风速的随机变化调整系统的风能利用系数Cp。在给定条件下，当风速为8 m/s～12 m/s时，Cp为0.423 3～0.434 2。仿真结果表明，在随机风工况下，Cp能够进行自适应调整，验证了仿真模型的可行性和有效性。由阶跃风工况和随机风工况的仿真结果可知，直驱式风力发电机控制系统仿真模型能够有效模拟在不同工况下系统对风速的响应过程，为系统的性能分析和优化控制提供可靠的理论基础。

4 结论

本文分别探讨了风力机和永磁同步发电机数学模型，并构建基于MATLAB/Simulink的风力机仿真模型和永磁同步发电机仿真模型，进而构建直驱式风力发电机控制系统整机仿真模型。在阶跃风工况和随机风工况下，对直驱式风力发电机控制系统进行仿真，得到在2种工况下系统的风能利用系数。仿真结果表明，在2种工况下建立的控制系统能够快速追踪风速变化，仿真模型能够有效仿真在不同工况下系统对风速的响应过程，仿真结果准确、可靠，能够为系统的性能分析和控制过程优化提供理论依据。但是，单一的仿真平台存在局限性。未来可以结合数模混合仿真技术，用数字仿真装置和物理仿真装置共同模拟电力系统，充分发挥各平台的优势，完成电力系统的跨平台、多平台高效仿真。

参考文献

[1]MAHSEREDJIAN J，DINAVAHI V，MARTINEZ J A.Simulation

tools for electromagnetic transients in power systems： Overview and challenges[J].IEEE Transactions on power delivery，2009，24（3）：1657-1669.

[2]张锁魁.基于Matlab/Simulink含风电的电力系统混沌特性研究[J].电力科学与工程，2014，30（7）：27-31.

[3]裴丽娜，孙东旭.基于Matlab Simulink的风电变桨控制系统动态数学模型和仿真研究[J].电气工程学报，2019，14（2）：66-70.

[4]KARAAGAC U，MAHSEREDJIAN J，GAGNON R，et al.

A generic EMT-type model for wind parks with permanent magnet

synchronous generator full size converter wind turbines[J].IEEE Power

and energy technology systems journal，2019，6（3）：131-141.

[5]TREVISAN A S，EL-DEIB A A，GAGNON R，et al.Field validated generic EMT-type model of a full converter wind turbine based on a gearless externally excited synchronous generator[J].IEEE Transactions on power delivery，2018，33（5）：2284-2293.

[6]王叶，杨微，兰涌森，等.大型海上风力发电机组最佳叶尖速比控制参数自适应整定方法[J].船舶工程，2019，41（增刊1）：334-336，340.

[7]常波.基于Matlab/Simulink的直驱式永磁风力发电系统的建模与仿真[D].南京：南京理工大学，2012.