新课标背景下小学分数教材体系的重塑

摘 要 分数是小学数学公认的学习难点。现行分数教材存在分数概念与整数概念缺乏实质贯通、分数运算与整数运算缺乏整体沟通、分数认识与分数运算缺乏系统融通等问题。在新课标实施、新教材修订的背景下，重塑小学分数教材体系，是教材修订者面临的一大挑战，也是一线教师关注的热点问题。前移简单分数乘除，促进分数认识与运算系统融通；强化分数度量意义，实现分数概念与整数概念本质贯通；运用计数单位工具，推动分数运算向整数运算整体转化，可以实现对小学分数教材体系的重塑。

关 键 词 新教材；新课标；分数与运算；教材体系

分数是小学数学公认的学习难点，也是《义务教育数学课程标准（2022年版）》（以下简称《新课标》）的改革重点。重塑分数内容的教材体系，以充分体现新课标改革精神、有效化解分数学习难点，是教材修订者面临的一大挑战，也是一线教师关注的热点问题。本文从反思现行分数教材、研读《新课标》出发，在合理吸收中外分数教材及其研究成果的基础上，提出小学分数教材体系重塑的构想。

一、 现实反思：我国小学分数教材的主要问题

1.分数概念与整数概念缺乏实质贯通，导致整数知识向分数迁移不畅

分数概念的内涵非常丰富。我国现行小学数学教材中，分数主要包括比率、度量和除法三种意义。

分数的比率意义，意即将一个整体均分成若干等份，分数即为所表示的部分量（一等份或几等份）与整体的比率；分数的度量意义，意即将均分整体得到的单位分数（一等分）作为度量单位，分数即为所表示的量用单位分数测量所得的结果，也即分数表示单位分数的迭代（累加）结果（即为单位分数的个数）；分数的除法意义，意即将分数视为两个整数相除所得的商。

虽然比率意义是分数意义生成的根本[1]，但度量意义更能体现分数作为数的本质意义[2]。在分数的比率意义中，整体就是用作比较的标准量，实质上被当成了计数单位，也即分数可以表示成比率与计数单位的乘积。但比率一般不是整数，所以分数的比率表征与整数的计数模式（即整数都可表示成计数单位与所含个数的乘积）不相一致。而在分数的度量意义中，单位分数被当成了计数单位，也即分数可以表示成计数单位与所含个数的乘积，所以分数的度量表征与整数的计数模式一致，即与整数一样都是数（shǔ）的结果，因此，分数的度量意义更能体现分数作为数的本质意义。

但我国现行各种版本小学数学教材中，过分强调比率意义、相对忽视度量意义，导致一些教师和学生将分数的意义等同于分数的比率意义。因为分数概念与整数概念未能实质贯通，造成整数知识向分数知识迁移受阻。

2.分数运算与整数运算缺乏整体沟通，导致分数乘除算法未能数学化

整数运算法则本是分数运算法则的知识基础和重要支撑，但我国现行各种版本小学数学教材除分数加减运算外，在分数乘除运算法则的探索中，未能将其与整数乘除整体沟通。

现行各种版本的小学数学教材都将分数乘除运算内容安排在第三学段，除“分数乘整数”“分数除以整数”等特殊情形外，对“分数乘分数”“数（整数、分数）除以分数”等一般情形的算法探索主要依赖直观和情境，而非基于分数概念和逻辑规则，将其转化为整数运算。如对于“分数乘分数”，现行教材大多通过对长方形模型进行两次均分，借助直观操作得出算法；对于“数（整数、分数）除以分数”，现行教材大多通过均分操作或速度模型，借助具体情境得出算法。

对直观操作和具体情境的过度依赖，不仅在思维层次上明显滞后于第三学段学生的认知发展水平，而且得到的算法未能达到数学结论应该具有的一般性要求，即数学化，其算理也未能实现与整数运算本质上的一致性[3]。

3.分数认识与分数运算缺乏系统融通，导致分数内容的教学低质高耗

“数的认识与数的运算具有密切的联系”“数的认识是数的运算的基础，通过数的运算有助于学生更好地认识数。”[4]但《义务教育数学课程标准（2011年版）》将分数的认识与分数的运算分别归入“数的认识”“数的运算”两个学习主题，导致在内容安排与教学实施上，分数的认识与运算缺乏系统融通和必要呼应，造成分数内容教学低质高耗。

一方面，在分数学习的第一阶段（3～4年级），内容安排主要集中于分数的初步认识，除了借助面积或数线等分数直观模型，安排了分母不超过10的同分母分数加减运算外，分数的其他运算概未提及。因缺少足够数量和类型的分数运算体验，不少学生对分数的理解停留在分数比率意义的初始阶段。由于对分数的度量意义缺乏认知，他们常常无法解释现实生活中常见的非标准形式分数。如某同学在满分为100的数学考试中得到85分，不少学生并不认可85是一个分数。因为它取的是分数的度量意义，没有分数的标准外形，即分子、分母及分数线，所以一些学生不予认可。另一方面，分数学习的第二阶段（5～6年级），在分数乘除运算法则的探索中，由于未能将其建立在分数概念本质意义（即计数单位的个数）的基础之上，致使整数乘除运算法则的支撑作用不能充分发挥，导致分数乘除算法的探索只能从原始的直观实物（模型）均分情境起步，极大影响了教学效率。

二、课标研读：小学分数课程内容的改革要点

1.确立素养导向的课程目标

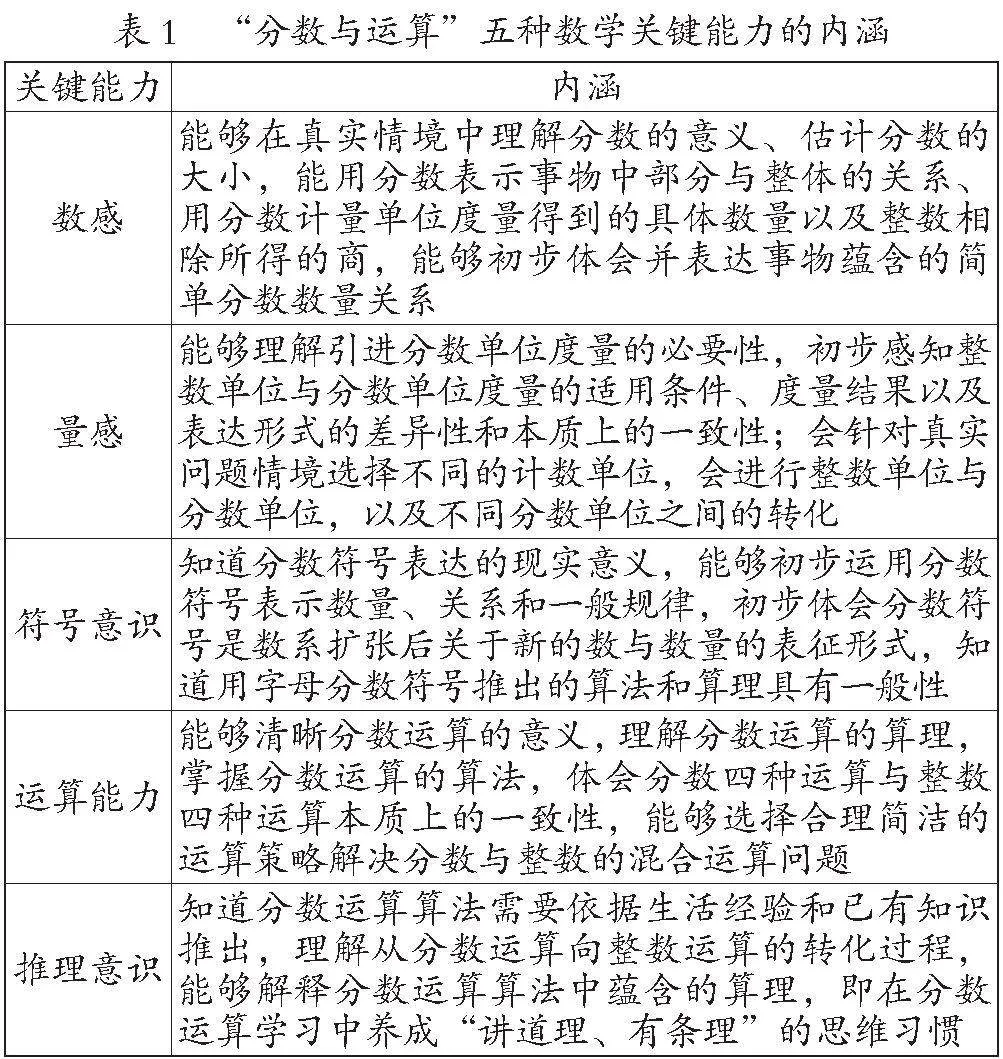
《新课标》确立了以“三会”为核心素养导向的课程目标，“把学生的数学学习提升到对现实世界的观察、思考与表达的新境界，使得数学课程目标直接指向学生未来社会生活和职场情境中的思维模式和行事方式”[5]。在“分数与运算”教学中，“三会”主要表现为数感、量感、符号意识、运算能力、推理意识五种数学关键能力（见表1）。

因此，创设面向现实世界的问题情境，让学生“在探索真实情境所蕴含的关系中”[6]，逐步发展以上五个数学关键能力为重点的“三会”核心素养，是《新课标》对小学分数教学目标提出的新要求。

2.构建整体贯通的内容结构

结构化整合是新课标关于课程内容组织的改革重点[7]。新课标将数与代数中的“数的认识”“数的运算”合并为一个主题“数与运算”，并提出“感悟数的概念本质上的一致性”“感悟数的运算以及运算之间的关系”“体会数的运算本质上的一致性”[8]（简称“两感悟、一体会”）等具体要求，就是对数与代数内容进行结构化整合的重要体现。具体到“分数与运算”，“两感悟、一体会”就是要求感悟分数概念与整数、小数概念的一致性，以及分数四则运算之间的关系，体会分数运算与整数、小数运算本质上的一致性，构建“整”“分”“小”数概念纵向贯通、“加”“减”“乘”“除”四则运算横向融通的“分数与运算”内容结构。

3.突出计数单位的基础作用

计数单位是建立数的概念的基础，数的概念又是进行数的运算的基础，也即计数单位在“数与运算”中具有基础性作用。《新课标》在“分数与运算”的第一阶段增加了“感悟分数单位”、第二阶段增加了“感悟计数单位”，而分数单位本质上就是分数的计数单位，因此，增加上述内容就是为了突出计数单位的基础性作用。一方面，借助分数的计数单位，每一个分数都可视为分数计数单位的累加结果，也即分数单位的个数，分数概念也就因此获得了与整数概念本质上的一致性；另一方面，运用分数的计数单位，可将分数的四则运算顺利转化为整数的四则运算，分数运算也就因此获得了与整数运算本质上的一致性。

三、体系重塑：小学分数教材内容的基本构想

1.在内容架构上，前移简单分数乘除，促进分数认识与分数运算的系统融通

现行分数教材中分数的认识与分数的运算分属两个学习主题，两者之间缺乏必要呼应。由于分数认识与分数运算的内在联系被削弱，导致分数知识的学习低质高耗。因此，小学分数教材内容架构的重塑重点是促进分数认识与分数运算的系统融通。

依据将“数的认识”与“数的运算”合并为“数与运算”的内容重组思路，以及对3～4年级学生认知发展阶段的基本判断，可将5～6年级 “分数乘整数”与“整数乘分数”（积为真分数）、“同分母分数相除”（除数分子能够整除被除数分子）、“分数除以整数”等简单的分数乘除内容前移至3～4年级。通过前移上述内容对分数教材内容架构进行重塑，既具有可行性又具有科学性。

2=4，也即“同分母分数相除，用两个分数的分子直接相除”。在实际教学中，可借助实物（模型）的均分操作，将相对抽象的分数单位用具象易感的一等份实物（模型）“小块（片）”代替。借助这样的实体“小块（片）”，抽象的分数乘除运算问题就变为赋予具体情境的整数乘除运算问题，完全能够被3～4年级学生理解和接受。

之所以说前移上述运算具有科学性，是因为适当采用螺旋式方式呈现课程内容是小学数学课程的一个重要理念[9]，前移简单的分数乘除内容，不仅可为后续分数运算教学进行必要铺垫，分散5～6年级分数运算的学习难点，提高5～6年级分数内容的教学层次，还可使3～4年级学生借助简单分数四则运算法则的探索过程，获得对分数概念多重含义的全面体验，促进分数认识与分数运算的整体融合。

2.在分数认识中，强化分数度量意义，实现分数概念与整数概念的本质贯通

现行分数教材因未能实现分数与整数概念的实质贯通，导致整数知识向分数迁移不畅。因此，小学分数教材分数认识的重塑重点是实现分数概念与整数概念的本质贯通。

关于分数概念教材的已有研究，主要分歧在于分数概念的引入方式以及应该强化分数的何种意义。

在分数概念的引入方式上，虽然有学者建议从“商”定义入手，以此为核心逐步给出分数的其他定义[10]。但中外现行各种教材几乎都以“比率”（“份数”“部分/整体”）定义作为分数学习的起点。从数学的观点看，“商”的定义源自整数除法推广的需要，也是创造分数的内在动力，用它引入分数定义似乎更为科学。但从认识的角度看，学生在接受正式的分数教育前，已经具备了分割计数的生活经验，借助分割计数的直观操作引入分数，更容易完成个体对分数概念的初步构建。因此，沿用现行教材以部分/整体的“比率”定义引入分数更为可行。

在应该着重强调的分数意义方面，各国不同版本教材存在差异：中、美等国教材突出“比率”意义，日本、新加坡等国教材重视“度量”意义[11]。但学者们对这个问题的看法比较一致，即要强化分数的度量意义。如不宜过分强调“份数”（“比率”）定义，在数直线上对分数作几何解释（“度量”定义）非常重要[12]；认识分数之初强调“比率”意义会给学生学习带来困难，要强化分数作为数（量）的涵义[13]，等等。

事实上，分数的度量意义，是沟通分数各种表征形式、促进分数理解的有力工具。从分数度量意义的视角去观察，分数概念与整数概念在本质上具有一致性，它们都可视作计数单位的迭代（累加）结果。因此，强化分数的度量意义，可以实现分数与整数的概念贯通，打通整数知识向分数知识迁移的通道，把“整数偏向”[14]对儿童学习分数的抑制因素，转化为整数知识对儿童分数学习的支撑因素，进而提高分数学习的质量和效率。

强化分数度量意义遇到的现实问题是，教学时间从何而来？现行教材分数比率意义的时间安排较为充裕，但压缩其教学时间，可能会影响小学生对分数比率意义的理解。由于单位“1”概念的引入，导致小学生理解分数的比率意义变得困难。根据本文第一部分的分析，在分数比率意义中，被均分的整体实质上被当作了单位量，即用来计数的比较标准，将其称为单位“1”本身没有问题，但要让小学生在更短时间内，理解整体所具有的“单位”属性，客观上并不容易。

一个可行的做法是，在分数比率意义教学中，删除单位“1”的概念，为分数度量意义的强化腾出时间。事实上，单位“1”概念对分数的比率意义并非不可或缺。如现行北师大版、沪教版等教材在表达分数的比率意义时，就没有出现单位“1”而是直接使用“整体”这个概念。如果没有单位“1”，有些教师可能担心，在后续解决与一个整体比率有关的分数应用题时，小学生不能理解为什么可将整体视为“1”。其实，借助与整体比率有关的具体问题情境，让小学生明白这一点并不难。因为说到一个量相对于一个整体的比率时，实质上是将这个整体作为比较标准，看这个量占整体的几分之几。求整体相对于自身的比率，就是将自身作为比较标准，用整体与自身相比。不管问题情境中的整体被分成了多少等份，表示整体比率的分数中分子与分母都相等，都是将均分整体得到的各个等份全部取出的总份数，也即整体相对于自身的比率为“1”，因此可将整体视为“1”。

分数度量意义的强化，消除了分数概念与整数概念之间的隔膜，使得分数问题转化成整数问题成为可能。但要顺利实现上述转化，最大的挑战来自分数的计数单位。因为分数的计数单位与整数的计数单位内在性质不同，整数的任意两个相邻计数单位之间具有统一的十进关系，而分数的计数单位之间没有这样的进率关系。因此，根据分数的度量意义，虽然分数问题一般都可转化为整数问题，但对于含有两个以上不同计数单位的分数问题，如何处理计数单位，往往成为能否成功解决问题的关键。

3.在分数运算中，运用计数单位工具，推动分数运算向整数运算的整体转化

现行分数教材因分数运算与整数运算缺乏整体沟通，导致分数乘除算法未能实现数学化。因此，小学分数运算教材的重塑重点是实现分数乘除算法的数学化。

关于分数运算教材的已有研究，重点指向分数除法。在实现分数除法算法数学化方面，主要有三种思路[15]：第一种（日本教材），先讨论“分数除以整数（整数能够整除分子）”这一特殊情形，再依次将“分数除以整数（整数不能整除分子）”转化为“分数除以整数（整数能够整除分子）”（分数的分子与分母同时乘以整数）、“数（整数、分数）除以分数”转化为“分数除以整数”（被除数与除数同时乘以除数分数的分母）；第二种（美国教材），先讨论“同分母分数相除”（借助分数的计数单位，转化为整数包含除法，参见本文第三部分（一）），再依次将“整数除以分数”化为“同分母分数相除”（整数写成与除数分数分母相同的分数）、“异分母分数相除”化为“同分母分数相除”（通分）；第三种（学者观点），先通过形式化的逻辑推理得出：“在整数除法中，除以一个数等于乘以这个数的倒数”（简要过程：由“被除数÷除数=？”得到“被除数=？×除数”；由“被除数×除数的倒数=？×除数×除数的倒数”得到“被除数×除数的倒数=？”，从而有“被除数÷除数=被除数×除数的倒数”），再将这个结论推广到分数除法中去。

上述三种思路虽然都能实现分数除法算法的数学化，但第一、三种思路主要依据相关的数学关系、性质及基本事实，属于基于逻辑规则的抽象化形式推演；第二种思路直接运用计数单位将分数化为“整数”，从而将分数除法转化为整数除法，属于对已有运算模式的关联性意义转换。两者比较，虽然第一、三种思路能够训练和发展学生的抽象思维能力，但第二种思路更能实现对分数概念本质的深度认识，更能体会分数与整数除法本质的一致性，更能感悟分数除法算法与分数加减算法思考方法的相似性。因而是重塑分数除法内容的理想选择。

作为《新课标》在“分数与运算”中着重强调的课程内容，计数单位是分析和研究分数运算的绝佳工具。运用这个工具，可以推动分数运算向整数运算的整体转化，充分体现分数与整数四则运算本质的一致性。以分数乘法为例，说明运用计数单位推动分数运算向整数运算转化的基本思路，并据此实现分数乘法算法的数学化，完成对分数乘法教材内容的重塑。下面按分数学习的两个阶段分别陈述：

第一阶段（3～4年级），安排“分数乘整数”“整数乘分数”（积为真分数）等特殊情形。借助计数单位，将其转化为整数相关运算，具体的转化思路与同分母分数除法类似，参见本文第三部分（一）。

对小学分数教材体系的重塑，为分数教学落实《新课标》精神提供了重要支撑。在教学实施中还需要建立分数学习内容与五种数学关键能力的关联，确立核心素养立意的学科育人思维。只有这样，以五种数学关键能力为主要表现的“三会”导向课程目标才可能在“分数与运算”学习中有效实现。

参考文献

[1] Kieren T E.The rational number construct：Its elements and mechanisms[J].Recent Research on Nunber Learning，1980：125-149.

[2] 丁锐，卫冰倩，Ron Tzur，等.分数度量意义发展的认知根基及轨迹：分数图式进阶理论[J].数学教育学报，2021，30（03）：64-72.

[3][11][15] 赵莉，王春英，史宁中.分数概念表述和分数除法运算的比较研究及其对教学的启示[J].数学教育学报，2021，30（03）：46-51.

[4][6][7][8][9] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022：20，11，3，18，3.

[5] 孙国春.《义务教育数学课程标准（2022年版）》的改革意涵探析——以核心素养为逻辑基点[J].课程·教材·教法，2022，42（12）：39-46.

[10] 蒲淑萍.“中国 美国 新加坡”小学数学教材中的“分数定义”[J].数学教育学报，2013，22（04）：21–24+70.

[12] 张奠宙.分数的定义[Ｊ].小学教学：数学版，2010（01）：48-49.

[13] 陈蓓，章飞.分数意义建构的顺序及对教科书设计的建议[J].数学教育学报，2018，27（04）：58–61.

[14] 刘春晖，辛自强.分数认知的“整数偏向”研究：理论与方法[J].心理科学进展，2010，18（01）：65-74.